우주선 설계 및 운용의 기법[편집 | 원본 편집]
실제 우주탐사의 역사 또는 궤도역학의 연구에서 검증된 기법으로서, KSP 플레이에 적용할 수 있다.
오베르트의 법칙[편집 | 원본 편집]
케플러의 제3법칙에 의해, 같은 천체의 중력권에서 공전할 때는 고도가 낮으면 낮을수록 속력이 빨라지게 된다.[1]
그런데 로켓 엔진은 언제나 일정한 추진력을 제공한다. (힘은 운동량의 변화량으로 정의되는데 운동량은 매 순간순간의 질량 곱하기 속도벡터로 정의된다. 그런데 로켓의 질량은 매 순간순간마다 연료를 소모시키면서 줄어들므로, 언제나 일정한 추진력을 내는 로켓 엔진에 의해 로켓 본체는 매 시간마다 점점 커지는 가속도로 가속된다.[2])
그리고 로켓의 운동 에너지는 1/2mv^2 즉 속력의 제곱에 비례한다. 그런 상황에서 로켓 엔진은 언제나 일정한 추진력을 제공하기 (즉 언제나 각 순간에서의 질량 곱하기 속도를 동일한 비율로 높여주기) 때문에 낮은 고도에서 엔진을 키면 높은 고도에서 엔진을 킬 때보다, 같은 추진력을 같은 시간동안 작용하고서도 운동에너지를 더 많이 얻는 결과가 나오게 된다.[3][4]
이 이야기가 오베르트의 법칙이라고 해서 우주개발 전공하는 사람들은 꼬꼬마 시절부터 귀에 못이 박히도록 듣는 이야기다. 그 때문에, 우주선을 띄울 땐 어디로 가는 거든간에 일단 커빈 저궤도[5]를 먼저 형성을 하고 나서 다른 데로 떠나게 된다.
Gravity Turn[편집 | 원본 편집]
이 오베르트의 법칙 때문에, ICBM 말고 우주에 나갈려고 쏘는 로켓은 일단 맨 처음엔 닥치고 지구 저궤도 형성부터 하려고 든다. 당연히 이는 KSP에서도 마찬가지다.
그런데 궤도를 형성을 하려면 당연하게도 80km 도달해서 로켓을 갑자기 확 꺾는 것보다는 커빈 대기권에서부터 이미 조금씩 조금씩 pitch를 낮춰가면서 최종적으로 80km 고도에서 로켓이 지표면에 평행하도록 하는 게 효율적이고 안전하다. 이렇게 조금씩 조금씩 pitch를 낮춰가는 과정을 Gravity Turn이라고 부른다.
Mechjeb을 깔면 Gravity Turn을 자동으로 수행해주는 기능이 생기는데, 이건 처음에 입력한대로만 닥치고 턴해주는 기능이고 각각 로켓마다 최적의 Gravity Turn 궤도는 다르므로, 자신이 주로 쓰는 로켓에 맞는 Gravity Turn를 찾는 게 중요하다. (그러지 않고 그냥 ΔV 좀 더 쓰겠다고 해도 말리진 않는다.) 근데 그것도 막 로켓 한대한대마다 Gravity Turn 궤도를 다 따로 찾아야 되는 수준은 아니고, 어차피 KSP에서 로켓을 설계하는 사람은 한 명이므로 결국 로켓들마다 최적의 Gravity Turn 궤도는 거의 비슷비슷한 수준에서 놀게 된다.
... 라고 하면 KSP 게임 내에서 통용되는 기법이고, 실제 Gravity Turn이라고 하면 처음에 5도 정도 확 꺾은 다음에 (킥턴이라고 함) 그 다음에는 중력으로 로켓이 쓰러지는 가속도와 엔진이 뿜어내는 가속도를 정확히 맞춰서 저절로 각도를 맞추게 하는 게 Gravity Turn이다. (로켓이 중력 받고 쓰러지면서 그 힘으로 turn이 된다고 Gravity Turn이다) 네이버 KSP 카페의 무림고수가 쓴 글 링크.
Swing-By[편집 | 원본 편집]
간단하게 말해 목적지로 가는 길에 큰 행성이 있다면 그 행성의 중력을 이용해서 우주선을 가속하는 것. 대부분의 문헌에선 운동량 보존 법칙을 이용한 경우라고 설명하나, 사실은 힘의 관점으로 설명하는 것이 더 직관적이다.
실제로 우주선은 태양계 내에서만도 수많은 천체가 끌어당기는 만유(萬有)인력을 받지만, 행성 또는 항성[6]의 '충분히 가까이'서 움직이는 우주선의 운동궤적을 설명할 때는, (라그랑주 점 등의) 일부 예외적인 경우를 제외하면 자기가 스쳐 지나가는 그 행성이 작용하는 중력을 제외한 다른 중력은 무시해도 좋을 정도로 영향이 작아진다.[7] 때문에 행성에 '충분히 가까이' 위치한 우주선은, 그 대빵 행성 한 놈의 중력만 받고 움직이는 걸로 가정하고 서술해도 된다. (이렇게 충분히 가까운 공간을 Sphere Of Influence (SOI) 라고 부르며, KSP 게임의 다른 부분에서도 많이 등장하는 개념이므로 숙지하고 넘어가는 것이 좋다.)
이런 가정 하에서, 우주선의 매 순간순간의 운동 궤적을 '대빵 행성'이 그 순간 작용하는 중력의 방향에 평행한 성분과, 그에 수직한 성분으로 분리해 보자[8]. 물리학에서는 힘의 양 그 자체가 "매 순간순간마다 힘을 받는 물체의 운동량(질량 * 속도)의 변화량"으로 정의되므로 매 순간순간마다 우주선은 '대빵 행성'이 작용하는 중력의 방향에 평행한 방향으로만 가속된다.
여기서, '대빵 행성'을 스쳐지나가던(swing-by) 우주선이 '대빵 행성'의 SOI에 진입하기 전과 빠져나간 후의 우주선의 운동 에너지의 변화는 '대빵 행성'의 중력을 고려하지 않았을 때의 우주선의 궤적이 '대빵 행성'을 궤적이 오목한 부분에 두는가 볼록한 부분에 두는가에 따라서 달라진다.
- 궤적이 오목한 부분에 '대빵 행성'이 있었다면, '우주선의 매 순간순간의 궤적의 중력 방향에 평행한 성분'의 크기가 중력과 일치하는 방향에서 점점 커지는데 이 과정을 중력이 도와주는 모양새가 되므로 우주선은 '대빵 행성'의 SOI에 있는 동안 운동에너지가 점점 커진다.
- 궤적이 볼록한 부분에 '대빵 행성'이 있었다면, '우주선의 매 순간순간의 궤적의 중력 방향에 평행한 성분'의 크기가 중력과 일치하는 방향에서 점점 작아지는데 이 과정을 중력이 방해하는 모양새가 되므로 우주선의 '대빵 행성'의 SOI에 있는 동안 운동에너지가 점점 작아지는 것이다.
이 원리를 이용해서, 우주선의 궤적이 행성을 감싸는 방향으로 스쳐 지나가도록 궤도를 설정하면 우주선의 속력이 무지막지하게 늘어나는 것이다. 여기다가 오베르트의 법칙까지 끼얹으면 ㅎㄷㄷ...
실제 우주탐사 역사상 수많은 심우주 탐사선이 스윙바이 기법으로 가속했으며, 보이저 2호는 목성, 토성, 천왕성, 해왕성이 너무 적절한 위치에 늘어서 있었던 최적의 기회를 이용해서 저 4개 행성 모두에서 스윙바이를 시전한 결과 현재 "인류가 만든 물체 중에서 가장 빠른 속도로 움직이는 물체"의 영원한 본좌 자리를 지키고 있다. 다만 단점이라면 스윙바이는 (적절하게 시전되었을 때) 운동에너지의 변화만 보장한다는 것이지 운동 궤적의 방향은 철저히 천문에 맡겨야 한다는 것으로, KSP에서 외행성을 방문할 때 시전하기에는 조금 어려운 감이 있다고 하겠다. NASA에서는 모든 천체의 궤적을 슈퍼컴에 입력해서 계산을 때렸다고 하지만, 아직까지 KSP 게임에선 그런 계산을 수행해 주는 앱은 없어서... 현실의 우주탐사에서도 스윙바이를 시전한 경우는 보이저 탐사선이나 파이어니어 탐사선 등 아예 외계인들 사는 심우주로 던져버리려고 쏜 우주선들의 경우에서 시전했다.[9]
Aerobraking[편집 | 원본 편집]
대기권이 있는 천체에 착륙할 경우 대기마찰을 이용해서 감속하면 연료를 매우 아낄 수 있는데 이 기법을 Aerobraking[10]이라고 부른다. 뮌이나 민무스에서 커빈에 재돌입하는 경우 궤도 최저점을 30km 상공에 맞춰주면 매우 적절한 가속도로 감속되면서, 낙하산을 단 몇백미터 상공에서 펴도 될 정도로 적절히 부드럽게 착륙할 수 있다.
그러나 정식발매되면서 재돌입시에 공기마찰로 열이 발생하는 점이 구현되었기 때문에 Heatshield로 과열을 막아줘야 하고, 과열이 심해지면 폭발한다(!!!) 한번에 감속하려고 하지 말고 수차례로 나눠서 감속하는게 좋다. 위에서도 뮌이나 민무스에서 커빈으로 돌아올 때 Aerobraking을 위한 고도를 30km정도를 쓸 수 있지, 줄이나 드레스같은 외행성에서 커빈에 재돌입할때 30km로 설정하면 폭발할 수도 있다.
아스파라거스 기법[편집 | 원본 편집]
연료통 여러 개를 수수깡 다발처럼 이어붙인 뒤 그 연료통들을 전부 배관으로 연결해서, 앞의 연료통에 빈 공긴이 생기면 뒤의 연료통에서 빨아오는 식으로 연료통을 순차적으로 무게중심을 맞추면서(대칭-2,3,4,6,8개씩) 조심스럽게 떨구면서 가는 기법. 그렇게 다발로 묶어놓은 연료통이 아스파라거스 다발처럼 생겼다고 아스파라거스 기법인데, 순우리말로는 '수수깡 기법'으로 순화할 여지가 있다고 하겠다. (실제로 원자론 극초기에 나온 J.J.톰슨의 '푸딩 건포도 모형'이 대한화학회에 의해 '백설기 콩떡 모형'으로 순화된 바 있기도 하다.)
설명만 들어보면 되게 맹해 보이는 기법이지만 오히려 이게 극강의 연료 효율을 자랑한다고 한다. 이브에 착륙했다가 커빈으로 귀환까지 하는 우주선들은 거의 전부 아스파라거스 기법으로 설계돼 있다. 현실의 우주선에 아스파라거스 기법이 없는 건 위험해서라는 단 한 가지 이유밖에 없다고 하니...정확히는 많은 수의 로켓이 소모하는 막대한 양의 연료를 효과적으로 공급해 주는 시스템의 개발이 어렵고, 많은 수의 로켓을 이용함으로서 증가하는 실패확률을 감당하느니 대형로켓 하나를 쓰는 편이 현실적으로 간편하기 때문이다. KSP에서는 연료배관 하나면 모든 연료공급이 끝나고, 별도의 모드를 설치하지 않는 한 로켓의 작동실패가 일어나는 일이 없으므로(실제로 부품을 일정 확률로 고장내는 모드가 있다!) 아스파라거스 형 로켓을 사용하기에 이상적인 환경이 제공되어 있는 셈이다.
이게 무슨 원리인가 하면, 연료를 다쓰고 남은 빈 연료탱크는 그 자체로 불필요한 짐 (아무 기능도 없으므로)이 되어서 우주선의 가속을 방해하니, 주 목적인 연료를 다쓰면 그 탱크를 버리는 것이다. 가능하면 많이 나눠서 다쓴 연료탱크를 여러번 분리하면 좋지만, 너무 자잘하게 구성하면 우주선의 구조 자체가 불안정해질수 있으므로 적절히 나눠서 하면 된다.
아폴로 우주선 형식[편집 | 원본 편집]
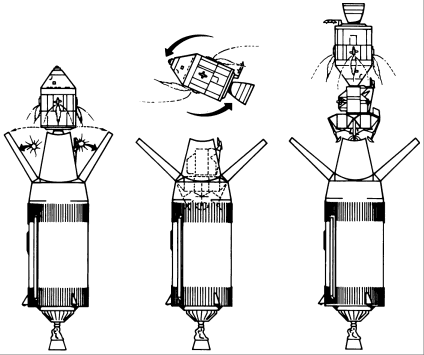
Procedural Fairing이란 모드가 깔려 있어야 게임에서 수월히 재현할 수 있는 형식으로
- 로켓을 하단의 추진부 - 중단의 착륙선 - 상단의 사령선/기계선 순서대로 조립한 뒤 (중단은 Procedural Fairing 모드의 페어링으로 감싸둔다)
- 커빈 궤도에 올라가는 데까지는 하단의 추진부로 올라가고 나서
- 궤도상에서 3단분리해서, 하단은 버리고 상단의 도킹포트를 열어서 뒤로 돌아 중단의 착륙선과 키스한다.
- 이후 목표 행성까지는 이렇게 키스한 상태에서 상단 사령선/기계선의 로켓을 사용해서 도착하고
- 목표 행성의 궤도에 진입한 뒤엔 착륙선을 분리해서 탐사를 수행한 뒤
- 탐사를 마치면 착륙선의 하단부는 버리고 조종실만 분리해서는 그 행성 궤도에서 대기하고 있던 사령선/기계선의 궤도로 도약하고 다시 키스하여 사령선/기계선에 데이터를 넘겨주고 착륙선 탑승 인원도 사령선/기계선으로 돌아와
- 사령선/기계선에 남아 있는 연료를 사용해서 커빈끼지 귀환하는 방식이다.
이런 짓거리까지 재현해냈다.
1.0버전 부터는 페어링이 추가되어 stock부품으로 구현하기가 한층 수월해졌다.
다만 국내 KSP 커뮤니티에서는 목표 천체 궤도까지 갔다오는 데 필요한 추력을 담당하는 우주선(사령선/기계선)과 목표 천체 표면까지 갔다오는 데 필요한 추력을 담당하는 우주선(착륙선)이 서로 나뉘어 있으면서 궤도에서 재합체를 하는 형식의 우주선은 전부 아폴로 형식이라고 부르는듯하다.
KSP에서 우주탐사를 할 때도 아폴로 형식이 자주 이용되는데, 고전적으로 저명한 방식을 오마주한다는 이유도 있겠지만 그냥 아폴로 형식이 가장 실용적이어서란 이유도 꽤 있다. KSP 커뮤니티에서는 일단 커빈 궤도에 올라간 뒤부터는 재돌입 이전까지 그 뒤의 모든 일을 단분리 없이 수행하는 탐사선도 자주 보이는데, 그런 탐사선들은 위성에 착륙할 때 매우 거추장스러운 부대부품까지 같이 들고 착륙해야 하기 때문에 착륙이 매우 어려워지는 것이 보통이다. 사실 착륙만이 문제가 아니다.
- 착륙선이 귀환선까지 겸하므로 커빈을 탈출하기 위해 붙여야 하는 로켓의 덩치가 엄청나게 커진다. 현실에서 꼴랑 그 작은 아폴로 우주선을 쏘겠다고 만들었던 로켓의 크기가 어느 정도였는지를 생각해 보고, 아폴로 계획 이후 그 어떤 로켓도 새턴 5호만큼의 육중함을 갖추지 않았다는 것을 떠올려보자. 날릴 물건이 커지면 로켓의 기본적인 규모가 확 늘어난다.
- 우주공간에서 우주선의 제어에 들어가는 연료+추력이 쌍으로 증가한다. 목표한 행성으로 가는 궤도를 만들고, 궤도에 들어가기 위해 역분사를 하는 등 비행 내내 분사할 일이 생기는데, 덩치가 클수록 그만큼 더 많은 연료와 추력이 필요하다.
- 앞서 언급된 부분이지만 착륙 과정에서 걸리는 부하가 산으로 간다. 역추진 로켓이든, 날개든, 낙하산이든 착륙시켜야하는 물건의 덩치가 커질수록 더 많이 혹은 더 강하게 달아줘야한다. 결국 로켓의 덩치가 커지고, 이 문제는 위의 두 문제를 더 증가시킨다. 당연한 이야기지만 행성에서 탈출하는데 걸리는 부하도 높아진다.
실제로도 아폴로 계획 초기에 '로켓 하나로 모든 임무를 한큐에 수행하자'라는 안이 고려되었는데, 이 당시에 나사에서 그린 착륙선 스케치는 그것 자체가 이미 하나의 거대한 로켓이였다.(...) 이후 현재의 아폴로 우주선과 같은 착륙선을 별도로 두는 안이 채택되어서 실제 임무에 사용되었다. 그리고 착륙선이 작을 수록 착륙/귀환에 드는 공도 줄어들기 때문에 거의 극한의 감량이 시도되었고 최종적으로는 아예 착륙선마저 2단 분리를 하는 안에다가 (그래서 달 착륙선 밑둥이 지금도 달에 남아 있어서 거기다가 레이저를 쏘면 레이저가 반사돼서 온다. 물론 KSP 게임 내에선 착륙선 단분리까지 재현하는 경우는 드물다.) 착륙선은 전화박스 몇개를 붙인 크기의 생활 공간에, 호일 몇장 수준의 벽체(발로 벽을 차면 우주선이 뚫릴 위험이 있었을 정도로 얇았다!)를 지닌 아담한 물건이 되었다. 초기 구상당시에는 도킹용 해치도 두 개에 여러 개의 큰 유리창을 가지고 있었지만, 무게 문제로 도킹용 해치 하나, 작은 유리창 두개로 축소되었다. 이 양반들 한번은 진지하게 '그냥 유리창 다 빼버리면 안되나?ㅇㅅㅇ'라는 생각까지 해봤었다는 듯. 머큐리 시절처럼 잠망경 달게?
커빈 궤도에서 사령선/기계선과 착륙선이 도킹하는 건 어차피 분리한 그 자리에서 다시 합체하는 거라 별 스킬은 필요가 없지만, 착륙선이 임무를 수행하고 난 뒤 궤도상의 사령선/기계선에 다시 도킹하는 건 Hohmann Transfer라는 상당한 고급의 스킬을 필요로 한다. 그럼에도, 서로 지근거리까지 접근하는 것(랑데부)과 거기서 운전을 잘 해서 서로 합체하는 것(도킹)은 또 다른 문제다 (...) 상당히 많은 초보들이 첫 우주탐사에서 좌절하는 게 바로 착륙선 조종실과 사령선을 도킹시키는 과정이다.
빡시다고 걱정하지는 말자. 나사에서도 처음에 저 안을 보고는 '지금 랑데뷰도 안 되는데 우주공간에서 도킹만 3번 하자고요?'라며 슬쩍 멘붕했었으니까. 이 기술을 익히기 위해 처음에는 우주선 두대의 랑데뷰 부터 시작해서 하나하나 연습해 나갔고, 결국 아폴로 계획 내내 랑데뷰/도킹 작업을 별 무리없이 해낼 수 있게 되었다.물론 우리는 이 양반들과는 달리 커벌들을 우주에 흩뿌리면서 배우겠지만. 물론 KSP 게임에 있어서도, 궤도역학적으로 유의미할 정도로 멀리 떨어진 우주선의 도킹을 능숙하게 해낼 수 있을 실력을 갖췄다면 KSP에서 다른 유저들의 도움이 필요할 정도는 지났다고 어깨 피고 다닐 수 있다.
호만 전이 (Hohmann Transfer)[편집 | 원본 편집]
이 호만 전이 궤도를 직접 설정하는 용자도 있는 모양이지만 대부분은 Mechjeb이란 모드의 호만 전이 궤도 설정 기능을 이용하는데, 직접 설정하든 멬젭으로 설정하든 궤도역학에서는 상대 우주선이 멀다고 속도를 높여서 따라잡으려다가는 우주선의 역학적 에너지가 높아져서 내 궤도의 고도가 높아지게 되니 (두 우주선이 이미 매우 가까워서 그냥 지상의 상식으로 가속해도 오차가 없을 상황이 되어야, 혹은 우주선이 dV, TWR, 선회 성능이 셋 다 초월적으로 좋아야 저런 저주받을 법칙에서 벗어날 수 있게 된다) 궤도에 대기하고 있는 사령선으로 돌아가는 것도 결국 착륙선과 사령선의 상대적 위치관계가 딱 맞아떨어질 때를 기다려서 도약해야지만 궤도에서 몇바퀴 도는 일을 피할 수 있다는 얘기다 (...) 그리고 바로 그런 이유로 호만 전이를 하기 전에 착륙선이 형성할 궤도는 기다리고 있는 사령선의 궤도와 같은 평면에 속하는 한에서 최대한 차이나게 설정하는 게 맞는 방법이다. 궤도가 차이가 많이 나야 궤도상에서 갖는 속도의 차이도 많이 나고 그래야 궤도의 위상[11]이 맞아떨어질 기회도 많이 생기기 때문.
SSTO (Single Stage To Orbit)[편집 | 원본 편집]
사전적으로는 단분리 없이 안정된 저궤도를 형성할 수 있는 우주선 모두를 일컫는 말이지만, 실무적으로는 보통 비행기의 형상을 한 우주선 즉 성층권 하부까지 초음속 제트엔진으로 가속했다가 그 위에서부터 로켓엔진으로 추진하는 방식으로 궤도를 형성하는 우주선을 가리킨다. 현실에서는 아직 실용화된 바가 없지만 KSP에선 중수와 고수를 가르는 기준이 바로 SSTO에 있다고 할 정도로 보편화되어 있다.
"일반적으로 커뮤니티에서 말해지는 SSTO"가 로켓에 대해서 갖는 장점은, 로켓은 깡추력으로 씹어야 하는 대기권 하층부 구간을 SSTO는 제트엔진과 날개의 힘으로 오히려 델타V를 버는 구간으로 이용할 수 있다는 점이다. 그래서 로켓에 비해서보다 총중량 - 연료 비율을 훨씬 적게 맞추고서도 대기권을 탈출할 수도 있다. 다만 단점은 '총중량 대 연료비율을 로켓보다 매우 적게 맞춰도 대기권을 탈출할 수 있다'란 점이 역으로 작용해서 SSTO 자체의 무게가 커지면 (단분리를 해서 무게를 줄일 수 있는 로켓과는 달리) 그 무거운 무게를 처음부터 끝까지 들고 가야 한다는 것과, 대기권 상층부만 가도 제트엔진이 벌써 작동불능이 되기 때문에 제트엔진과 로켓엔진을 같이 달이줘야 한다는 점이다.[12]
사실 단분리 없이 궤도를 형성할 수만 있으면 되기 때문에 일반적인 로켓 모양이어도 상관 없다. 이 경우는 조종이 더 쉽고 균형 맞추는 것도 쉽다. 물론 간지가 안나서 만드는 사람이 별로 없다
나눠 쏴서 궤도상에서 합체[편집 | 원본 편집]
로켓의 성능을 표기하는 용어로 payload라는 게 있다. 그 로켓을 쏴서, 모행성 저궤도에 몇 톤의 물체까지 올려놓을 수 있는지를 표기하는 수치다. 이걸 높일 수 있는 데까지는 높이는 게 좋지만, 대부분의 우주정거장 등 넘사벽급으로 큰 물체는 로켓 한 대로 쏘아서 보내려면 그 로켓을 건조하는 것마저 불가능할 정도까지 될 수가 있다. 그런 경우, 물체를 여러 파트로 나눠서 로켓 여러 대에 나눠서 쏘아보낸 뒤 전부 다 궤도에 올리고 나서 합체를 시키는 것. ISS가 바로 이렇게 지어졌는데, ISS는 세계 각국에서 분담해서 설계 및 제작하고 각자 쏴서 합체시킨 거라 여기서 말하는 거랑은 느낌이 다르다.
참고로 그 커다란 물체를 다른 행성 궤도에 올려놓을 거라면, 그 행성 궤도로 올라갈 때까지 각자 추진해서 온 다음에 목표 행성의 궤도상에서 합체한다.
KSP에서 말하는 건, 나눠 쏘는 부품들이랑 각자 쏘아올리는 로켓들을 전부 한 회사에서 만들어서 문자 그대로 동시에 쏘아올리는 것. 이 동영상을 보면 무슨 느낌인지 알 수 있다.[13] 실제로 NASA에서도 달보다 더 멀리 있는 천체를 유인탐사할 때는 이런 식으로 할 계획이라고 한다.
참고로 이 기법을 쓴다면, 나눠 쏘는 "부품" 중에 우주비행사 그 자체도 부품으로 들어간다. 역시 현실성 추구를 위한 장잉정신 중 하나인데, 이렇게 분리해서 궤도에 올린 뒤 합체시켜야 할 정도로 무지막지하게 큰 우주선이라면 그 우주선을 분리시켰을 때의 각각의 조립체도 사람이 타고 올라가는 우주선보다 넘사벽으로 커지는 경우가 많은데, 이렇게 payload가 커지면 로켓이 궤도상에 올라가면서 포고 현상 등으로 불안정한 궤도를 그릴 가능성이 커지기 때문이고, 당연하지만 기계는 충분히 버틸 수 있는 정도의 가속도라도 사람은 못 버티는 경우가 훨씬 많다. 달 탐사하는 규모에서야 우주선이랑 사람을 같이 넣고 쏴도 사람이 무리하지 않을 수 있었지만, 현실에서도 화성 정도만 갈려고 해도 아폴로 우주선의 몇 배 크기는 되는 로켓을 여러 대를 쏴서 합체시켜야 한다. (달까지 가는 데는 왕복 1주일 가량이면 됐지만, 화성까지는 가는 데만 6달은 걸린다. 왕복 1년이 넘는 시간동안 우주선에서 숙식을 해결해야 되니까, 최소 미르 우주정거장만한 우주선으로 왔다갔다해야 하는 것.[14][15])
궤도 연락선[편집 | 원본 편집]
때문에 이렇게 대형 우주선을 조립체로 분리해서 쏜 다음에 궤도상에서 합체시키는 경우에는, 우주선의 조립체는 무인 조종으로 따로 쏴서 올리고,[16] 사람은 "딱 사람을 궤도에 올릴 정도만 되는" 작은 우주선으로 따로 쏴서 궤도에서 탑승하는 방식으로 운용한다. 그렇다고 그 남은 조그만 우주선도 버리는 건 당연히 아니고(...) 커다란 우주선에 도킹시켜 놨다가 임무가 끝났을 때 드랍포드 용도로 재활용한다. 현실에서 소유즈 (유인 우주선)이 이 용도로 절찬리에 애용되고 있다 (...) 실제로 ISS 우주정거장에 소유즈 우주선이 모듈로서 항시 결합되어 있다.
물론 NASA에서는 우주비행사가 우주에 한 번 다녀올 때마다 우주선을 1회용으로 버리는 것은 아깝다고 생각했는지 여러 번을 궤도에 왔다갔다하면서 재활용할 수 있는 우주 왕복선을 개발했지만, 현실에서는 우주 왕복선을 쏘는 것보다 차라리 소유즈 같은 1회용 우주선을 매 임무 때마다 찍어내는 게 더 경제적이라는 결론이 나서 오히려 우주 왕복선 프로젝트가 폐기되었다. 하지만 어차피 돈이 남아돌고, 우주개발 말고 다른 데는 예산을 투자할 필요도 없고, 필요하면 돈 나가는 옵션을 아예 끌 수도 있는 KSP에서는, 소유즈 방식을 택할 건지 우주 왕복선 방식을 택할 건지 본인 취향껏 선택하면 된다. 근데 KSP에선 우주 왕복선 만드는 게 피똥싸게 어렵다[17]
우주선 설계 및 운용의 기법 Ⅱ[편집 | 원본 편집]
여기서는 실제 우주탐사의 역사 또는 궤도역학의 연구에서 검증된 기법과 달리 KSP 라는 게임에 있어서 적용할 수 있는 것들을 소개한다.
문단 뒤의 (M)은 이 기법을 활용하기 위해 반드시 어떤 모드를 설치해야 한다는 것을 의미하며, (C)는 이 기법 자체가 버그 또는 그에 준하는 현상을 이용한 기법이라는 것을 의미한다. 아무 기호가 없는 기법이 순정에서 정정당당하게 쓸 수 있는 기법.
페어링 지지대 (M)[편집 | 원본 편집]
- 필수 모드 : Procedural Fairing
Procedural Fairing 모드가 있어야 쓸 수 있는 기법으로, 페어링 알 껍질에도 스트럿이 붙는 것을 이용한 기법이다. 화물과 페어링 껍질을 스트럿으로 묶어 주는 것만으로도 로켓의 안정성이 비약적으로 상승한다!
노즈콘 내 수납공간 (M)[편집 | 원본 편집]
- 필수 모드 : Procedural Parts
Procedural Parts 모드는 연료통, 전지, 고체로켓 등등을 형태와 크기를 자유롭게 설정할 수 있는 부품을 추가해주는 모드인데, 이 부품이 취할 수 있는 모양 중 Smooth Cone이란 모양이 있다. 이 형태로 직경과 모양을 적절하게 설정해주면, 자유로운 형상의 노즈콘을 만들 수 있을뿐만 아니라 노즈콘 내부를 수납공간으로 활용할 수 있게 된다.
게임을 위해서 생략 내지 변경된 물리현상[편집 | 원본 편집]
SOI (Sphere Of Influence) 개념의 확장[편집 | 원본 편집]
3체문제 떡밥을 죽여버림으로써 게임의 모델을 더 말끔하게 만들기(...) 위해, KSP의 우주에서는 모든 우주선들은 자기가 있는 지점에서 가장 중력을 크게 작용하는 천체 단 하나의 중력만을 받고 움직이는 것으로 물리연산이 단순화되었다. 그러니만큼 우주선들끼리 작용하는 중력은 매우 당연히 무시된다.
이 때문에 3체문제나 라그랑주 포인트, 중력 트랙터 같은 현재 절찬리에 연구되고 있는 우주물리학 떡밥 상당수를 재현할 수 없게 되었다.
하지만 어쩔 수 없는 게, 아직까지 현대 물리학에서 3체 이상 n체문제의 일반해는 존재하지 않으므로, 현실의 우주처럼 우주선들이 모든 천체의 중력을 동시에 받는 걸로 시뮬레이션을 하면 일단 게임 엔진이 세이브파일을 작성하는 데 매우 큰 애로사항이 꽃피게 된다 (...) 우주 모든 물체의 운동궤적과 운동량을 알면 그걸로 쫙 시뮬레이션을 돌려서 몇백억년 뒤 미래의 모습까지 예언할 수 있을 거라고 믿는 사상을 라플라스의 악마라고 하는데, 이게 최종적으로 관짝에 갇힌 건 양자역학이 태동하고서부터지만 이미 양자역학을 쌩까도 인류는 서로 엇비슷한 질량의 꼴랑 별 3개가 움직이는 현상도 완전히 예측을 못한다 (...)
현재 게임에서는 모든 우주선의 거동을 우주선<->모천체의 쌍체문제로 간략화시켰기에 일단 우주선이 궤도를 완성만 하면 궤도가 매우 깔끔하게 형성돼서 영원히 보존되는데 (그리고 게임 내 세이브 파일에서는 그런 정보들이 모두 기록된다) 우주선이 모든 천체와 중력을 주고받는[18] 식으로 시뮬레이션을 해버리면 지금 안정한 궤도가 몇십년 뒤에도 그대로 있을지 없을지 여부를 장담할 수 없게 된다.[19] 현실에서 대기마찰도 뭣도 안 받는 인공위성이 자세제어 로켓을 다는 이유가 바로 이 때문인데, 현실에선 KSP와 달리 인공위성 궤도에 어쩌다 한 번씩 스쳐지나가는 달의 중력까지 영향을 미치기 때문에 인공위성을 좀 오래 돌리다 보면 그런 오차들이 누적돼서 궤도가 점점 틀어지고 인공위성이 임무수행 궤도를 벗어날 수도 있게 된다. 어차피 인공위성에 실린 전자장비도 수명이 있기 때문에, 딱 그 수명동안 궤도 오차를 보정할 수 있는 만큼의 monopropellant를 실어서 보내는 것.
네임드 유저들의 플레이 영상[편집 | 원본 편집]
- ROBBAZ의 플레이 영상
전혀 도움 안 되잖아
각주
- ↑ 케플러 제3법칙 (조화의 법칙) : 같은 모천체를 공전하는 임의의 천체의 공전 주기의 제곱은 그 천체를 공전하는 궤도의 장축 반지름의 세제곱에 비례한다.
- ↑ 말이 어렵지 Mechjeb 깔고 로켓 몇 번만 쏴보면 바로 알게 된다.
- ↑ 근데 이거 물리학적으로 당연한 얘기다. 에너지의 변화량은 물체가 받은 일의 양으로 정의되는데, 일의 양은 "힘 곱하기 물체가 힘의 방향으로 움직인 거리"로 정의된다. 낮은 고도에서는 로켓이 더 빠른 속도로 움직인다고 했으므로, 같은 추력으로 같은 시간을 추진하면 당연히 그 추력을 로켓이 더 먼 거리를 움직일 때까지 받게 된다. 따라서 낮은 고도에서 로켓을 추진했을 때가 높은 고도에서 추진했을 때보다 운동에너지를 더 얻는 게 당연하다.
- ↑ 앞 주석이 잘 이해가 가지 않는다면, 로켓의 뒤에서 로켓이 매 순간순간 움직이는 속도만큼 로켓을 쫓아다니면서 로켓을 손으로 민다고 생각해보자. 로켓 엔진의 원리가 바로 이것이다.
- ↑ 약자로 LKO라고 하며, 커빈 대기권에 마찰을 안 받는 한도 내에서 궤도반지름이 가장 짧은 궤도를 말한다. 커빈의 대기권은 70km 고도까지 뻗어 있다. 커뮤니티에서 통용되는 LKO는 80km 고도지만, 많은 사람들은 그보다 더 낮은 고도로 최초 궤도를 맞춘다.
- ↑ 이하부터는 그냥 '행성'이라고만 부르기로 한다. KSP에선 항성에다가 스윙바이를 시켜야 할 상황은 애초에 나오질 않으니까.
- ↑ 행성의 정의 : 항성 주위를 자체적으로 일정한 궤도로 공전하고, 자신의 중력으로 말미암아 구형 또는 그에 가까운 모양을 유지할 수 있을 정도로 크며, 자신의 궤도 안에서 지배적인 영향을 독자적으로 미칠 수 있을만큼 크면서도, 자체적으로 핵융합 반응을 일으킬 정도로 크지는 않은 천체를 일컫는 말.
- ↑ 궤적을 벡터분해한다는 게 사실은 되게 사변적이고 비직관적인 설명이지만, 여기서는 우주선의 에너지(운동 궤적과는 아무 상관이 없는 물리량이다)가 중요하고 대빵 행성의 중력(그니까 힘)이 기준이 되는 상황이므로 부득이하게 힘에 맞춰 궤적을 분해한다.
- ↑ 농담이 아니라, 과학자들도 진지하게 믿지는 않았겠지만 파이어니어 11호에서는 외계인들이 그 우주선을 줏으면 읽으라고 지구의 정보를 담은 레코드판까지 실어 보냈을 정도였다.
- ↑ aero- : 대기/공기, braking : 브레이크
- ↑ 위상(phase)이란, 주기 운동을 하는 물체의 운동에서 그 물체의 궤적이 "한 주기의 어느 부분에" 있는지를 말하는 개념이다. 주기 운동의 대표적인 예가 파동(개별 질점 입장에서 파동을 봤을 때)이고 '한 주기 안에서의 위치 관계'를 따져야 할 일도 파동에서 많이 나오는고로 위상이란 단어 자체가 파동에서 자주 언급되지만, 원칙대로라면 어떤 형태의 주기 운동에도 쓸 수 있다. 실제로 단진자 운동이나 등속 원운동에서 위상이라는 말을 쓰는 용법도 있다.
- ↑ 엔진 하나로 대기권에선 제트, 산소가 없으면 로켓으로 변형할 수 있는 R.A.P.I.E.R 엔진이란 것도 있으나 이 녀석은 연비도 출력도 심각하게 낮다.
- ↑ 참고로 이 영상에서 페이로드를 커빈 궤도상에 올린 다음에 쓰고 남은 로켓을 커빈에 다시 담그는 것은 일종의 롤플레이로, 실제 우주개발에 있어서 우주쓰레기를 무분별하게 발생시키면 그 우주쓰레기들이 지구상에서 고리를 이뤄버려 우주발사체가 우주로 나가지 못하게 된다는 현상인 케슬러 신드롬이 발생할 수 있기 때문이다. (우주쓰레기가 설마 "그 정도로 빽빽해지겠느냐" 하겠는데, 토성의 고리도 실제로는 소행성 및 암석 무더기임을 생각해 보면 우주쓰레기로 인해 지구에 '고리가 생긴다'라고 하는 서술은 우주궤도공학 쪽에선 별로 틀린 서술도 아니다.) KSP에서는 어차피 우주센터가 플레이어가 일하는 곳 한 곳밖에 없고, 케슬러 신드롬이 날만큼 발사체를 많이 쏴보기도 전에 웬만해선 게임에 질리게 될 것이므로(...) 사실 게임 내적으로는 별 상관은 없지만, "현실의 우주센터라면 이렇게 하지는 않을 것이다" 라는 생각에서 비롯된 일종의 장잉정신이라고 보면 된다.
- ↑ 일단 미르 우주정거장 정도만 돼도 최대 체류기록 1년을 넘기긴 했다. 그 무렵 소련이 망해서 우주비행사를 귀환시킬 우주선을 쏠 돈이 없어서 어쩔 수 없이 넘긴 거긴 하지만 그래도 넘긴 건 넘긴 거다 (...) 다만 미르는 자세제어 용도의 추진기관만 갖고 있었지만, 화성으로 갈 우주선이라면 화성에서 지구까지 왔다갔다 하는 데 필요한 ΔV를 충당할 수 있는 엔진과 연료통까지 장착되어야 하므로, 이게 단순 우주정거장보다 얼마나 더 커져야 할지는 알아서 생각해보도록 하자.
- ↑ 그리고 혹시 "가는 데 시간이 오래 걸리면 속도를 높여서 빨리 가면 되는 거 아니야?"라고 할 사람들이 있을 텐데, 빨리 가겠다고 속도를 높이면 나중에 화성 궤도 진입할 때 피똥을 싼다 (...) 속도를 높일 때도, 나중에 다시 속도를 줄일 때도 dV를 소모하니 연료가 더 많이 필요해지고, 화성 궤도 진입하는 단계에서 속도가 지나치게 높으면 화성을 스쳐 지나가버리기 전에 감속을 해야 하니 TWR도 더 높아져야 한다. 뭐 이렇게 골치가 아프냐고? NASA 과학자도 이 게임 하면서 피똥 싼 적이 한두번이 아니라고 하니 그냥 받아들이자 (...)
- ↑ 그래서 RemoteTech 모드를 깔았다면 테크 풀리자마자 통신위성 만들어서 커빈 궤도에 위성통신망 설치하는 것이 가장 급선무가 된다. 참고 현실에서는 (이리듐 계획에서) 지구 전체를 커버하는 통신망을 만들겠다고 인공위성을 66개를 띄워야 했을 정도로 무지막지한 일이었지만 (그나마도 원안은 77개를 띄울 계획이었다!) RemoteTech 모드에서는 커빈의 직경에 비해 안테나의 성능이 무지막지하기 때문에 단 6대의 위성만 있으면 커빈 전역을 커버할 수 있고 그나마도 커빈 극지방에서 활동할 일이 거의 없음을 생각하면 적도궤도에만 단 3대의 통신위성으로 웬만한 관제수요는 다 해결이 된다.
- ↑ 정확히 말하면 재돌입시의 공기저항을 견뎌낼 수 있는 우주왕복선을 만들기도 어렵고 조종하기도 어렵다. 그래도 그나마 이건 항공기형 SSTO를 만들 수 있으면 같은 방법으로 해결되지만, 이 물건을 비대칭인 로켓에 걸고 쏴야 하는 단계에서 영혼까지 털리는 것이 보통이다.
- ↑ 뉴턴역학 제3법칙 (작용-반작용 법칙) 의 의미를 잘 생각해보자.
- ↑ 섭동이라고 하는데, 생각외로 큰 문제다. 우주선도 컴퓨터도 없을 시절 지구에서 망원경만 갖고 천왕성, 해왕성,
명왕성왜행성 134330을 발견한 게 바로 이 현상 때문에 행성들 공전궤도 틀어지는 걸 연구하면서였으니까.
| 쉽게 알 수 있는 학문 | |
|---|---|
| 쉽게 할 수 있는 취미 | |
| 창작 안내서 시리즈 | |
| 뭘헤매지 시리즈 | |
| 여행 시리즈 | |
| 연표 시리즈 | |
| 생활의 지혜 | |
| 리브레 기네스 | |
| 리브레 위키 | |
| 기타 | |