시리즈:수포자도 쉽게 알 수 있는 수학/해석기하학

수학이 정말 쉬워서 저 수포자 그만둡니다.

문서의 내용이 너무 쉬워서 머리속에 쏙쏙 들어옵니다.

이 문서는 쉽게 알 수 있다 시리즈이며, 집단연구 문서입니다.

이 문서에는 독자적으로 연구한 내용이 들어갑니다. 다른 사람의 의견을 존중하면서 무례하지 않도록 작성해 주시고, 의견 충돌 시 토론 문서에서 토론해 주세요.

도와주세요! 리브레 수학 선생님! 코너 바로가기

수포자도 쉽게 알 수 있는 수학 틀:토막글

개요

해석 기하란 좌표계를 이용하는 기하학이다. (반대되는 개념으로 좌표를 사용하지 않고 순수하게 도형의 성질만으로 답을 구하거나 명제를 증명하는 논증기하학이 있다.)

우리가 일반적으로 사용하는 평면좌표계에서는 각 점마다 정해진 좌표가 존재하고, 그 좌표의 값에 따라 선분의 길이 등이 명시적으로 표현되기 때문에 기하학 문제를 상당히 단순화시킬 수 있는 경우가 많다. 물론 이와는 반대로 선분의 길이를 각 끝점의 좌표로 계산하게 되면 피타고라스의 정리로부터 나오는 제곱근들이 난무하게 되어 논리는 어찌 되었는 계산은 매우 지저분해지는 경우가 상당수이다. 이외에 해석기하학의 장점은 직선, 곡선 등으로 이루어진 도형을 일차함수 등 함수의 그래프의 조합으로 표현할 수 있다는 것이다. 일반적인 고등학교 수학으세는 잘 나오지 않는 내용이지만, 경시 수학에서 나올 법한 '세 점이 한 직선 위에 있다는 것을 증명하라' 또는 '세 직선이 한 점에서 만난다는 것을 증명하라', '두 선분의 교점이 ~의 과정을 통해 구한 원의 중심임을 보여라' 등의 문제는 증명이 매우 쉬워지기도 한다. 도형의 성질만을 이용하는 경우와는 달리, 해석기하학에서는 '어느 직선 위에 있다=그 직선의 방정식을 만족한다', '여러 직선이 한 점에서 만난다=직선의 방정식을 연립하면 해가 하나다'가 성립하기 때문이다. 확인된 정보는 아니지만, 모 수학 강사에 따르면 한국수학올림피아드(KMO)애 출전한 학생들이 기하 문제를 전부 해석기하로 풀어제끼는 바람에 주최측인 대한수학회에서 해석기하를 사용한 풀이는 감점하기 시작했다는 이야기도 있다.

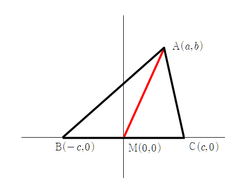
해석 기하의 유용함을 들 때 사용하는 설명은 중선 정리(또는 아폴로니우스의 정리, 파푸스의 중선 정리라는 이름은 우리나라하고 일본만 쓴다 카더라)를 예로 많이 든다.

좌표로 돌리고 풀면 쉽게 증명할 수 있다.

정리) [math]\displaystyle{ \operatorname{\overline {AB}^2+\overline {AC}^2=2(\overline {AM}^2+\overline {BM}^2)} }[/math]

증명) [math]\displaystyle{ \operatorname{\overline {AB}^2+\overline {AC}^2}= \{ (a+c)^2+b^2 \} + \{ (a-c)^2+b^2 \} =2a^2+2b^2+2c^2 }[/math] [math]\displaystyle{ 2a^2+2b^2+2c^2=2\{(a^2 + b^2) + c^2 \}=\operatorname{2(\overline {AM}^2+\overline {BM}^2)} }[/math]

그런데 왜 타원 방정식, 쌍곡선 방정식 이런 어려운 걸 푸냐고?? 쉽게 풀 수 있으니까 이제 어려운거 도전해야지!! 조삼모사???

다만 2018년부터 수학 교과 과정이 간소화되어 기하벡터 과목이 선택사항이 되면 더 이상 모든 수험생들이 이런 복잡한 문제와 씨름할 필요는 없을지도 모른다. 이과는 안 될 거야 아마

평면좌표

이차 곡선

여기에서는 포물선의 준선, 타원의 장축 또는 장축, 쌍곡선의 주축이 x축 또는 y축과 평행한 경우만을 다룬다.