편집 요약 없음 |
잔글편집 요약 없음 |
||
| 1번째 줄: | 1번째 줄: | ||
{{쉽게 알 수 있다 시리즈|수학이 정말 쉬워서 저 수포자 그만둡니다. | {{쉽게 알 수 있다 시리즈|수학이 정말 쉬워서 저 수포자 그만둡니다. | ||
|문서의 내용이 너무 쉬워서 머리속에 쏙쏙 들어옵니다. | |||
|수포자도 쉽게 알 수 있는 수학/질문|도와주세요! 리브레 수학 선생님! 코너 바로가기}} | |||
=== [[미분]] === | === [[미분]] === | ||
2015년 6월 8일 (월) 19:34 판
미분
미분이라는 것은 간단히 말하면 적분의 반대 개념이다. 그리고 적분은 미분의 반대 개념이다. 미분이 계산하기 편하기 때문에 먼저 배우는 경우가 많은데, 사실 직관적으로 원리를 설명하기 편리한 쪽은 도형의 넓이를 구한다던지 하는 데에 쓰이는 적분이다.

자동차가 0 m 의 출발선에서 출발해서, 1초 후에 1 m, 2초 후에 4 m, 3초 후에 9 m ... 를 간다고 해 보자. 그러면 10초 후에는 100 m 를 갔을 것이고, 속력을 계산해 보면 속력은 거리/시간 이니까 100 m / 10초 = 10 m/s 가 된다. 그런데 이건 '10초 동안의 평균 속력' 이지, '10초가 된 순간에 자동차 계기판에 찍힌 순간 속력' 은 아니다. 10초가 된 순간의 속력을 알고 싶으면 어떻게 해야 할까?
생각해 보면, 9초일 때 자동차의 위치는 81 m, 9.9초일 때는 98.01 m, 9.99초일 때는 99.8001 m...이다. 그러면 자동차의 속력은 (100 - 81 m)/(10 - 9초), (100 - 98.01 m)/(10 - 9.9초), (100 - 99.8001 m)/(10 - 9.99초)... 가 될 것이다. 앞에서 한 것과 비슷하지 않은가?
수식으로 정리해 보면, [math]\displaystyle{ \lim_{x \rightarrow 10}\frac{100 - x^2}{10 - x} }[/math]이다. 인수분해해서 계산하면
[math]\displaystyle{ \lim_{x \rightarrow 10}\frac{100 - x^2}{10 - x} = \lim_{x \rightarrow 10}\frac{(10 + x)(10 - x)}{10 - x} = \lim_{x \rightarrow 10}(10 + x) = 20 }[/math]
즉 10초가 된 순간의 자동차의 속력이 20 m/s 임을 함수의 극한을 이용해 구한 것이다. 이렇게 어떤 함수의 매 순간의 변화량을 함수의 극한을 통해 구하는 것이 미분이다.
이걸 좀더 일반화해 보자. 시간 x 초에서 자동차가 간 거리는 x2이다. 그러면 x 초에서의 속력을 알기 위해, x 보다 약간 작은 x - h 초를 생각해 보면, x - h 초일 때의 거리는 (x - h)2 가 될 것이고, 위에서 한 것처럼 순간 속력은 h 가 0 에 가까워져 x 와 x - h 가 아주 가까워질 때를 생각하면 된다.
[math]\displaystyle{ \lim_{h \rightarrow 0}\frac{x^2 - (x - h)^2}{x - (x - h)} = \lim_{h \rightarrow 0}\frac{x^2 - x^2 + 2hx - h^2}{h} = \lim_{h \rightarrow 0}(2x - h) = 2x }[/math]
따라서 x 초가 된 순간의 자동차의 속력은 2x m/s이다. 매번 9, 9.9, 9.99... 의 제곱을 구해서 100에서 빼고 나누고 하는 귀찮은 짓을 할 필요 없이, 이제 10초일 때의 속력은 20, 20초일 때는 40... 이렇게 바로 구할 수 있게 된 것이다! 이게 바로 '함수를 미분' 한 것이다.
미분이라는 것은 어떤 함수 [math]\displaystyle{ f(x) }[/math]가 있을 때 [math]\displaystyle{ (x, f(x)) }[/math]에서 [math]\displaystyle{ f(x) }[/math]와 접하는 선, 즉 접선의 기울기를 구할 때에 사용된다.
이를 어떻게 구하는지 보자. [math]\displaystyle{ f(x) }[/math] 함수 위의 두 점, [math]\displaystyle{ (a, f(a)) }[/math]와 [math]\displaystyle{ (b, f(b)) }[/math]를 지나는 선의 기울기는 다음과 같을 것이다.
기울기 : [math]\displaystyle{ \frac{f(b) - f(a)}{b-a} }[/math]
이를 그대로 적용해서, 점 [math]\displaystyle{ (x, f(x)) }[/math]와 그로부터 x축으로 [math]\displaystyle{ \Delta x }[/math]만큼 떨어진 [math]\displaystyle{ (x+\Delta x, f(x+\Delta x)) }[/math] 의 기울기를 표현하면 다음과 같을 것이다.
기울기 : [math]\displaystyle{ \frac{f(x+\Delta x) - f(x)}{ (x + \Delta x) - x} = \frac{f(x+\Delta x) - f(x)}{ \Delta x} }[/math]
이 때 [math]\displaystyle{ \Delta x }[/math]가 작아질수록 이 두 점을 연결하는 선은 점점 우리가 구하고자 하는 접선의 기울기에 가까워지게 된다. 따라서, 함수 [math]\displaystyle{ f(x) }[/math]의 접선의 기울기는 다음과 같이 표현할 수 있다.
접선의 기울기 : [math]\displaystyle{ \lim_{\Delta x\rightarrow 0}\frac{f(x+\Delta x) - f(x)}{ \Delta x} }[/math]
이를 함수 [math]\displaystyle{ f(x) }[/math]의 도함수라고 하며, [math]\displaystyle{ f'(x) }[/math] 또는 [math]\displaystyle{ \frac {\mathrm dy}{\mathrm dx} }[/math]라고 표기한다. 전자는 함수 [math]\displaystyle{ f(x) }[/math]의 도함수라는 것을 표현한 것이며, 후자는 접선의 기울기를 나타낸다는 것을 표현한 것이다. 문제에 따라서 편리한 표현방법을 사용하게 된다.
상수함수의 미분법
상수함수란 x의 값에 상관없이 항상 함숫값이 c로 일정한 함수다. 즉 [math]\displaystyle{ f(x)=c }[/math]인 함수가 있을 때, 도함수 [math]\displaystyle{ f'(x)=0 }[/math]이다. 미분계수가 그래프에서의 기울기를 뜻하므로, 직관적으로도 도함수는 항상 0임을 알 수 있다.
다항함수의 미분법
다항함수의 미분법은 아주 간단하다. 빼기, 곱하기만 할 수 있으면 누구나 할 수 있다. 물론 그 증명도 중요하지만 일단 계산법만 올려보자면 아래와 같다.
실수 n에 대해 함수 [math]\displaystyle{ {x}^{n} }[/math]의 도함수는 다음과 같다.
[math]\displaystyle{ ({x}^{n})'=n{x}^{n-1} }[/math].
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}({x}^{n})=n{x}^{n-1} }[/math]
n이 자연수일 때의 증명
다음과 같은 계산 과정을 통해서 자연수에 대해서 증명이 가능하고, 미분에 대한 지식 몇 가지만 추가하면 실수 n에 대해서 확장할 수 있다. 그러나 어렵다 싶으면 일단 그냥 암기해서 이용해도 문제없는 부분이다.
[math]\displaystyle{ \lim_{\Delta x\to 0} \frac{(x+\Delta x)^n - x^n}{\Delta x} = \lim_{\Delta x\rightarrow 0} \frac{nx^{n-1}\Delta x+\frac{n(n-1)}{2} x^{n-2}\Delta x^2 + ... + nx\Delta x^{n-1} + \Delta x^n }{\Delta x} }[/math]
[math]\displaystyle{ = \lim_{\Delta x \to 0} \left( nx^{n-1} + \frac{n(n-1)}{2} x^{n-2}\Delta x + ... + nx\Delta x^{n-1} + \Delta x^{n-1} \right) = nx^{n-1} }[/math]
[math]\displaystyle{ \Delta x }[/math]를 약분하고 [math]\displaystyle{ \Delta x }[/math]의 1차항 이상은 극한이 0으로 가므로 무시할 수 있어서, 위 함수의 도함수는 [math]\displaystyle{ n{x}^{n-1} }[/math]이 된다. 이것을 미분에 있어서의 Power Rule, 지수법칙이라고 부른다.
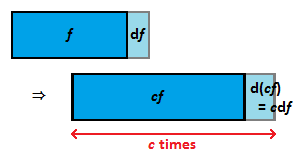
상수배
[math]\displaystyle{ (cf(x))'=c(f(x))' }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}(cf(x))=c\frac{\mathrm d}{\mathrm dx}(f(x)) }[/math]
그림에서 [math]\displaystyle{ \mathrm d(cf) = c\mathrm df }[/math]임을 알 수 있고, 양변을 [math]\displaystyle{ \mathrm dx }[/math]로 나눠 주면 [math]\displaystyle{ \frac{\mathrm d(cf)}{\mathrm dx} = c \frac{\mathrm df}{\mathrm dx} }[/math]가 되어 원하는 결과를 얻는다.
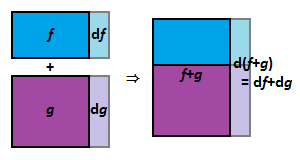
합차
[math]\displaystyle{ (f(x) \pm g(x))'=f'(x) \pm g'(x) }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}(f(x) \pm g(x))=\frac{\mathrm d}{\mathrm dx}(f(x)) \pm \frac{\mathrm d}{\mathrm dx}(g(x)) }[/math]
그림에서 [math]\displaystyle{ \mathrm d(f+g) = \mathrm df+\mathrm dg }[/math]임을 알 수 있고, 양변을 [math]\displaystyle{ \mathrm dx }[/math]로 나눠 주면 [math]\displaystyle{ \frac{\mathrm d(f+g)}{\mathrm dx} = \frac{\mathrm df}{\mathrm dx} + \frac{\mathrm dg}{\mathrm dx} }[/math]가 되어 원하는 결과를 얻는다.
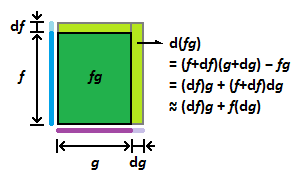
곱
[math]\displaystyle{ (f(x)g(x))'=f'(x)g(x)+f(x)g'(x) }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}(f(x)g(x))=\frac{\mathrm d}{\mathrm dx}(f(x))g(x)+f(x)\frac{\mathrm d}{\mathrm dx}(g(x)) }[/math]
그림에서 [math]\displaystyle{ \mathrm d(fg) = (\mathrm df)g+f(\mathrm dg) }[/math]임을 알 수 있고, 양변을 [math]\displaystyle{ \mathrm dx }[/math]로 나눠 주면 [math]\displaystyle{ \frac{\mathrm d(fg)}{\mathrm dx} = \frac{\mathrm df}{\mathrm dx} g + f \frac{\mathrm dg}{\mathrm dx} }[/math]가 되어 원하는 결과를 얻는다.
왜 [math]\displaystyle{ \mathrm df\mathrm dg }[/math]를 무시해도 되는지는 좀 설명이 필요하다. 지금 [math]\displaystyle{ \mathrm df }[/math]랑 [math]\displaystyle{ \mathrm dg }[/math] 모두 [math]\displaystyle{ \mathrm dx }[/math]가 줄어듦에 따라 같이 줄어든다. 따라서 [math]\displaystyle{ \mathrm df\mathrm dg }[/math]는 [math]\displaystyle{ \mathrm df }[/math]가 줄어드는 속도와 [math]\displaystyle{ \mathrm dg }[/math]가 줄어드는 속도의 영향을 중첩적으로 받아 훨씬 빨리 줄어들게 된다. 즉 [math]\displaystyle{ \mathrm df\mathrm dg }[/math]가 줄어드는 속도가 [math]\displaystyle{ \mathrm dx }[/math]가 줄어드는 속도보다 한층 빠르고, 따라서 무시해도 되는 것이다. 즉 [math]\displaystyle{ \mathrm df\mathrm dg }[/math]가 작아서 무시한다는 말은 좀 그렇고, 작긴 작은데 그 정도가 [math]\displaystyle{ \mathrm dx }[/math]보다 한층 더하기 때문에 무시해도 된다는 것이다.
합성함수
y=f(u)이고,u=g(x)이고 둘 다 미분가능하면.
[math]\displaystyle{ (f(g(x)))'=f'(g(x)) g'(x) }[/math]
[math]\displaystyle{ \frac{\mathrm dy}{\mathrm dx}=\frac{\mathrm dy}{\mathrm du}\times \frac{\mathrm du}{\mathrm dx} }[/math][2]
삼각함수
- 삼각함수 공식 외우기는 삼각함수 공식을 외워보자 참고.
사인
[math]\displaystyle{ color{asd} (\sin x)'=\cos x }[/math].
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}(\sin x)=\cos x }[/math].
코사인
[math]\displaystyle{ (\cos x)'=-\sin x }[/math].
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}(\cos x)=-\sin x }[/math].
탄젠트
[math]\displaystyle{ \color{asd} (\tan x)'={\sec }^{2} x }[/math].
[math]\displaystyle{ {\frac{\mathrm d}{\mathrm dx}(\tan x)={\sec }^{2} x} }[/math].
역함수
임의의 함수 [math]\displaystyle{ f(x) }[/math]의 역함수
[math]\displaystyle{ {{f}^{-1}(x)} }[/math] 가 존재하면.
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}({f}^{-1}(x))=\frac{1}{f'({f}^{-1}(x))} }[/math].
지수함수
[math]\displaystyle{ \color{#5140F2}{ (e^x)' = e^x} }[/math]
[math]\displaystyle{ \color{#5140F2}{ (a^x)' = a^x \ln a} }[/math]
[math]\displaystyle{ \color{#5140F2}{ \frac{\mathrm d}{\mathrm dx}e^x = e^x} }[/math]
[math]\displaystyle{ \color{#5140F2}{\frac{\mathrm d}{\mathrm dx}({a}^{x})={a}^{x}\ln a} }[/math].
[math]\displaystyle{ \color{#5140F2}{a\neq 1,a\gt 0} }[/math].
로그함수
[math]\displaystyle{ (\ln x)' = \frac{1}{x} }[/math]
[math]\displaystyle{ (\log_{a} x)' = \frac{1}{x \ln a} }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}\ln x = \frac{1}{x} }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx} \log_{a} x = \frac{1}{x \ln {a}} }[/math]
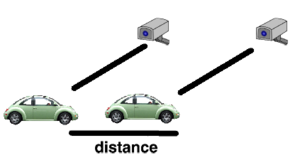
평균값 정리
도로교통 이야기로 잠시 넘어가보자. 구간단속은 일정 구간에서 평균 속도가 제한 속도를 위반하면 적발하는 단속 방법이다. 이전까지 쓰이던 지점단속에는 단속 대상자가 카메라 앞에서만 속도를 잠시 줄인 뒤 카메라에서 벗어나면 다시 과속을 할 수 있다는 문제가 있었다. 그러나 구간단속에서는 이런 꼼수가 원천 차단된다.
예를 들어 어떤 운전자의 차량이 적발 속도가 80km/h이고 길이가 1km인 구간단속 시작지점에 들어설 때 시속 60km으로 달리고 있었다고 가정하고 30초 후 끝지점으로 나올 때 여전히 시속 60km로 달리고 있었다고 가정하자. 이때 이 차량의 평균 속도는 120km/h이다. 이 결과는 단속구간에 있을 때 어느 순간 차량의 순간속도가 120km/h을 찍었다는 걸 의미한다. 지점단속으로는 단속에 걸리지 않지만 구간단속으로는 얄짤없이 단속에 걸리게 된다. 이 상황을 약간 추상화하면, 어느 구간에서 (구간 양끝 함수값의 차)/(구간 양끝점의 차)의 값과 같은 미분계수를 가지는 지점이 존재한다는 결론을 얻고, 이것이 바로 평균값 정리다. 물론 아무 때나 쓰면 곤란하고 평균값 정리가 성립하기 위한 조건들이 있으니, 더 자세히 알고 싶으면 항목을 참조하길.
적분
부정적분
문과생에게도 잘 알려져 있는 "적분은 미분 거꾸로, 미분은 적분 거꾸로"
상수배
[math]\displaystyle{ \color{#177636}{\int cf(x) dx=c\int f(x) dx} }[/math]
합차
[math]\displaystyle{ \color{#EE497F}{\int (f(x)\pm g(x)) dx=\int f(x) dx\pm\int g(x) dx} }[/math]
[math]\displaystyle{ \color{#FF00}{{x}^{n}} }[/math]
| 함수 | 역도함수(부정적분) | ||
|---|---|---|---|
| [math]\displaystyle{ \color{#FF00}{{x}^{n}} }[/math] | [math]\displaystyle{ \color{#FF00}{n \neq -1} }[/math] | [math]\displaystyle{ \color{#AC0FF}{\frac{{x}^{n+1}}{n+1}+C} }[/math] | |
| [math]\displaystyle{ \color{#FF00}{n = -1} }[/math] | [math]\displaystyle{ \color{#591759}{\ln |x|+C} }[/math] | ||
삼각함수
| 함수 | 역도함수(부정적분) | |
|---|---|---|
| [math]\displaystyle{ \color{#0ACFF}{\sin x} }[/math] | [math]\displaystyle{ \color{#156B94}{-\cos x +C} }[/math] | |
| [math]\displaystyle{ \color{#9D99}{\cos x} }[/math] | [math]\displaystyle{ \color{#9D9D9}{\sin x+C} }[/math] | |
| [math]\displaystyle{ \color{#996D9}{{\sec}^{2} x} }[/math][3] | [math]\displaystyle{ \color{#9D99}{\tan x+C} }[/math] | |
| [math]\displaystyle{ \color{#952D9}{{\csc}^{2} x} }[/math][4] | [math]\displaystyle{ \color{#99D9}{-\cot x+C} }[/math][5] | |
| [math]\displaystyle{ \color{#FF69AC}{\sec x \tan x} }[/math] | [math]\displaystyle{ \color{#FF69AC}{\sec x +C} }[/math] | |
| [math]\displaystyle{ \color{#059FF}{\csc x \cot x} }[/math] | [math]\displaystyle{ \color{#01952}{-\csc x +C} }[/math] | |
[math]\displaystyle{ \color{#173876}{{a}^{x},a\gt 0,a\neq 1} }[/math]
[math]\displaystyle{ \color{#B5107F}{\int {a}^{x} dx=\frac{{a}^{x}}{\ln a}+C} }[/math]
치환적분법
[math]\displaystyle{ \color{#177617}{\int f(x) dx=\int f(g(t))g'(t) dt} }[/math][6]
뭐 이렇기는 한데,미분의 합성함수의 미분법과는 달리 치환적분법은 모든 합성함수에 대해 적용할 수가 없다.
오히려 적용이 거의 안되는 함수가 훨씬 더 많다.
음 전혀 간단하지 않게 말하자면 [math]\displaystyle{ \color{#177617}{t} }[/math]=(
[math]\displaystyle{ \color{#177617}{x} }[/math]에 관한 적당한 함수)로 놓고
[math]\displaystyle{ \color{#177617}{x} }[/math]=([math]\displaystyle{ \color{#177617}{t} }[/math]에 관한 함수)로 적절히 변형한 다음에 위 식에 대입하자.
예시 1
[math]\displaystyle{ \color{#0ACFF}{\int {(2x+1)}^{3} dx} }[/math]
[math]\displaystyle{ \color{#0ACFF}{2x+1=t,f(x)={(2x+1)}^{3}} }[/math]로 놓자.
양변에 1을 빼면.
[math]\displaystyle{ \color{#0ACFF}{2x=t-1=g(t)} }[/math]
이제 양변을 2로 나누자.
[math]\displaystyle{ \color{#0ACFF}{x=\frac{t-1}{2}=g(t)} }[/math]
[math]\displaystyle{ \color{#0ACFF}{g'(t)=\frac{1}{2}=\frac{dx}{dt}} }[/math]
이제 [math]\displaystyle{ \color{#0ACFF}{f(x)} }[/math] 에 대입하면.
[math]\displaystyle{ \color{#0ACFF}{\int {((2\times \frac{t-1}{2} +1)}^{3}\times \frac{1}{2}) dt} }[/math]
[math]\displaystyle{ \color{#0ACFF}{\int \frac{1}{2}{t}^{3} dt} }[/math]
상수는 밖으로 빼내자.
[math]\displaystyle{ \color{#0ACFF}{\frac{1}{2} \int {t}^{3} dt} }[/math]
[math]\displaystyle{ \color{#0ACFF}{\frac{1}{2}\times \frac{1}{4}{t}^{4}+C} }[/math]
[math]\displaystyle{ \color{#0ACFF}{\frac{1}{8}{t}^{4}+C} }[/math]
[math]\displaystyle{ \color{#0ACFF}{t=2x+1} }[/math]이므로 [math]\displaystyle{ \color{#0ACFF}{t} }[/math]에 대입하자.
[math]\displaystyle{ \color{#0ACFF}{\frac{1}{8}{(2x+1)}^{4}+C} }[/math]
예시 2
[math]\displaystyle{ \color{#0059FF}{\int \tan x dx} }[/math]
[math]\displaystyle{ \color{#0059FF}{\int \frac{\sin x}{\cos x} dx} }[/math]
[math]\displaystyle{ \color{#0059FF}{\cos x=t,f(x)=\frac{\sin x}{\cos x}} }[/math]로 둡니다.
[math]\displaystyle{ \color{#0059FF}{x=g(t)} }[/math]꼴로 만들기 위해서 양변에
[math]\displaystyle{ \color{#0059FF}{\arccos x} }[/math][7]를 취합니다.
[math]\displaystyle{ \color{#0059FF}{\arccos t=x=g(t)} }[/math]
이제 [math]\displaystyle{ \color{#0059FF}{g'(t)=\frac{dx}{dt}} }[/math]를 구해봅시다.
수포자도 쉽게 알 수 있는 수학#역함수에서 [math]\displaystyle{ \color{#037FF}{f(x)=\cos x,f'(x)=-\sin x} }[/math]가 가 된다.
그러면 [math]\displaystyle{ \color{#0059FF}{\frac{d}{dx}(\arccos x)=\frac{1}{-\sin (\arccos x)}} }[/math]이 됩니다.
[math]\displaystyle{ \color{#0059FF}{\frac{d}{dx}(\arccos x)=\frac{1}{-\sin (\arccos x)}} }[/math]
[math]\displaystyle{ \color{#0059FF}{{\sin}^{2} (\arccos x)+{\cos}^{2} (\arccos x)=1} }[/math]
[math]\displaystyle{ \color{#0059FF}{{\sin}^{2} (\arccos x)+{x}^{2}=1} }[/math]
[math]\displaystyle{ \color{#0059FF}{{\sin}^{2} (\arccos x)=1-{x}^{2}} }[/math]
[math]\displaystyle{ \color{#0059FF}{{\sin} (\arccos x)=\pm \sqrt{1-{x}^{2}}} }[/math]
그런데 [math]\displaystyle{ \color{#0059FF}{0\leq \arccos x\leq \pi } }[/math]
[8]
이고 [math]\displaystyle{ \color{#0059FF}{0\leq \ x \leq \pi } }[/math]에서
[math]\displaystyle{ \color{#0059FF}{\sin x\geq 0} }[/math]이다.
따라서 [math]\displaystyle{ \color{#0059FF}{\sin (\arccos x)=\sqrt{1-{x}^{2}}} }[/math]이다.
따라서 [math]\displaystyle{ \color{#0059FF}{g'(t)=\frac{1}{-\sqrt{1-{t}^{2}}}} }[/math]입니다.
대입하면.
[math]\displaystyle{ \color{#0059FF}{\int \frac{-\sin (\arccos t)}{\cos (\arccos t)\times \sqrt{1-{t}^{2}}} dt} }[/math]
[math]\displaystyle{ \color{#0059FF}{\int \frac{-\sqrt{1-{t}^{2}}}{t\times \sqrt{1-{t}^{2}}} dt} }[/math]
[math]\displaystyle{ \color{#0059FF}{\int \frac{-1}{t} dt} }[/math]
[math]\displaystyle{ \color{#0059FF}{-\int \frac{1}{t} dt} }[/math]
[math]\displaystyle{ \color{#0059FF}{-\ln |t| +C} }[/math]
[math]\displaystyle{ \color{#0059FF}{t=\cos x} }[/math]이므로 대입합니다.
[math]\displaystyle{ \color{#0059FF}{-\ln |\cos x| +C} }[/math]
부분적분법
[math]\displaystyle{ \color{#C06AE9}{\int f(x)g'(x) dx=f(x)g(x)-\int f'(x)g(x)dx} }[/math]
로그함수,역삼각함수,다항함수,삼각함수,지수함수 중에서 가장 먼저의 것을
[math]\displaystyle{ \color{#C06AE9}{f(x)} }[/math]에 대입하고 나머지를
[math]\displaystyle{ \color{#C06AE9}{g'(x)} }[/math]에 대입하는 것이 좋다.
곱의 미분법 적분판이라고 볼 수 있...지만 만능은 전혀 아니다.
예시 1
[math]\displaystyle{ \color{#C06AE9}{\int x{e}^{x} dx} }[/math]
일단 다항함수인 [math]\displaystyle{ \color{#C06AE9}{x} }[/math]를
[math]\displaystyle{ \color{#C06AE9}{f(x)} }[/math]에 대입하고 지수함수인
[math]\displaystyle{ \color{#C06AE9}{{e}^{x}} }[/math]를 [math]\displaystyle{ \color{#C06AE9}{g'(x)} }[/math]에 대입한다.
[math]\displaystyle{ \color{#C06AE9}{g'(x)={e}^{x},g(x)={e}^{x}+C} }[/math]
[math]\displaystyle{ \color{#C06AE9}{f(x)=x,f'(x)=1} }[/math]
이제 대입하면.
[math]\displaystyle{ \color{#C06AE9}{x({e}^{x}+C)-\int ((1\times ({e}^{x}+C)) dx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{x{e}^{x}+Cx-\int {e}^{x} dx-\int C dx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{x{e}^{x}+Cx-{e}^{x}+D-Cx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{Cx} }[/math]끼리 소거됩니다.
[math]\displaystyle{ \color{#C06AE9}{x{e}^{x}-{e}^{x}+D} }[/math]
적당히 인수분해합니다.D는 C는 둘다 적분상수이므로 D를 C로 바꾸어도 됩니다.
예시 2
[math]\displaystyle{ \color{#C06AE9}{\int \log_{a} x dx(a\gt 0)} }[/math]
먼저 로그함수인
[math]\displaystyle{ \color{#C06AE9}{\log_{a} x dx(a\gt 0)} }[/math]
를 [math]\displaystyle{ \color{#C06AE9}{f(x)} }[/math]에 대입한다.
그 다음에 다항함수인 1[9]을
[math]\displaystyle{ \color{#C06AE9}{g'(x)} }[/math]에 대입합니다.
자,이제 [math]\displaystyle{ \color{#C06AE9}{g(x)=x+C} }[/math]입니다.
[math]\displaystyle{ \color{#C06AE9}{\frac{1}{x \ln a}=f'(x)} }[/math]입니다.
이제 대입합니다.
[math]\displaystyle{ \color{#C06AE9}{\int {\log }_{a} x dx=(x+C)\log _{a}x-\int (\frac{1}{x \ln a}(x+C))dx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int \log _{a}x dx=(x+C)\log _{a}x-\int (\frac{1}{\ln a}+\frac{C}{x\ln a})dx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int \log _{a}x dx=(x+C)\log _{a}x-\int \frac{1}{\ln a} dx-\int \frac{C}{x\ln a}dx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int \log _{a}x dx=(x+C)\log _{a}x-\int \frac{1}{\ln a} dx-\frac{C}{\ln a}\int \frac{1}{x}dx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int \log _{a}x dx=(x+C)\log _{a}x-\frac{x}{\ln a} -\frac{C}{\ln a}
\ln |x|+D} }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int {\log}_{a} x dx=x {\log}_{a} x +C{\log}_{a} x-\frac{x}{\ln a}-\frac{C\ln |x|}{\ln a}+D} }[/math]
[math]\displaystyle{ \color{#C06AE9}{x\gt 0,|x|=x,{\log}_{a} x = \frac{{\ln}{x}}{\ln a} } }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int {\log}_{a} x dx=x {\log}_{a} x +C\frac{\ln x}{\ln a}-\frac{x}{\ln a}-\frac{C\ln x}{\ln a}+D } }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int {\log}_{a} x dx=x {\log}_{a} x +\frac{C\ln x}{\ln a}-\frac{x}{\ln a}-\frac{C\ln x}{\ln a}+D } }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int {\log}_{a} x dx=x {\log}_{a} x -\frac{x}{\ln a}+D } }[/math]
[math]\displaystyle{ \color{#C06AE9}{D} }[/math]는 적분상수입니다.
끝입니다.
정적분
정적분이란 함수 y=f(x)와 닫힌 구간[a, b]로 둘러 싸인 도형의 넓이를 구하는 방법입니다.[10]
구분구적법
도형의 넓이나 입체의 부피를 다음과 같이 구할 수 있습니다.
- 주어진 도형을 충분히 작은 여러 개의 기본 도형[11]으로 나누고,
- 그 기본 도형의 넓이 또는 부피의 합을 구할 수 있는 식을 만들고[12]
- 2에서 구한 식에서 n->∞일 때의 극한값을 구하면 됩니다.
이것이 바로 구분구적법 입니다.
다음은 구분 구적법을 적용해서 도형의 넓이를 구한 것 입니다.
화면 확대가 필요합니다.도저히 작성자의 실력으로는 도형과 식들을 표현 할 수 없었다고 합니다.
여기까지가 구분구적법의 설명입니다. 하지만, 작성자가 구분구적법을 공부하실 위키러에게 드리고 싶은 말씀은, 수능에 않나온다고, 중요하지 않다고 막 넘기시지 마시고, 어떻게 해서 구분구적법이 나오게 되었는가? 즉, 구분구적법의 원리와 발상을 공부해 보시라는 것입니다.
정의
[math]\displaystyle{ \lim_{n\rightarrow \infty }\sum_{k=1}^{n}f(x_{k})\Delta x(\Delta x=\frac{b-a}{n},x_{k}=a+k\Delta x)=\int_{a}^{b}f(x)dx }[/math]
예제 1
[math]\displaystyle{ \int_{1}^{2} {x}^{2} dx }[/math]
[math]\displaystyle{ f(x)={x}^{2} }[/math]
[math]\displaystyle{ a=1,b=2,b-a=1 }[/math]
[math]\displaystyle{ \Delta x=\frac{1}{n},{x}_{k}=1+k\Delta x=1+\frac{k}{n} }[/math]
[math]\displaystyle{ \lim_{n\rightarrow \infty } \sum_{k=1}^{n}(1+\frac{k}{n})^2\frac{1}{n} }[/math]
[math]\displaystyle{ \lim_{n\rightarrow \infty } \sum_{k=1}^{n}(1+\frac{2k}{n}+\frac{k^{2}}{n^2})\frac{1}{n} }[/math]
[math]\displaystyle{ \lim_{n\rightarrow \infty } \sum_{k=1}^{n}(\frac{1}{n}+\frac{2k}{n^2}+\frac{k^{2}}{n^3}) }[/math]
[math]\displaystyle{ \lim_{n\rightarrow \infty }(\sum_{k=1}^{n}\frac{1}{n}+\sum_{k=1}^{n}\frac{2k}{n^2}+\sum_{k=1}^{n}\frac{{k}^{2}}{{n}^{3}}) }[/math]
[math]\displaystyle{ \lim_{n\rightarrow \infty }(\frac{1}{n}\sum_{k=1}^{n}1+\frac{2}{n^2}\sum_{k=1}^{n}k+\frac{1}{n^3}\sum_{k=1}^{n}{k}^{2}) }[/math]
그리고
[math]\displaystyle{ \sum_{k=1}^{n}k=\frac{n(n+1)}{2},\sum_{k=1}^{n}{k}^{2}=\frac{n(n+1)(2n+1)}{6} }[/math]
입니다.
[math]\displaystyle{ \lim_{n\rightarrow \infty }(1+\frac{2}{n^2}\frac{n(n+1)}{2}+\frac{1}{n^3}\frac{n(n+1)(2n+1)}{6}) }[/math]
[math]\displaystyle{ \lim_{n\rightarrow \infty }(1+\frac{n(n+1)}{n^2}+\frac{n(n+1)(2n+1)}{6n^3}) }[/math]
극한의 성질에 따라 세 식 모두 수렴하므로 각각 분리합니다.
[math]\displaystyle{ \lim_{n\rightarrow \infty }1+\lim_{n\rightarrow \infty }\frac{n(n+1)}{n^2}+\lim_{n\rightarrow \infty }\frac{n(n+1)(2n+1)}{6n^3} }[/math]
[math]\displaystyle{ 1+1+\frac{1}{3}=\frac{7}{3} }[/math]
미적분의 기본정리
[math]\displaystyle{ f(x) }[/math]가 닫힌구간 [math]\displaystyle{ [a,b] }[/math]에서 연속일 때, [math]\displaystyle{ \frac{d}{dx} \int_{a}^{b} f(t)\, dt=f(x) }[/math]이다.
닫힌구간 [math]\displaystyle{ [a,b] }[/math]에서 연속인 함수 [math]\displaystyle{ f(x) }[/math]의 한 부정적분을 [math]\displaystyle{ F(x) }[/math]라고 할 때,
[math]\displaystyle{ \int_{a}^{b} f(x) dx=F(b)-F(a) }[/math]
이 미적분의 기본정리를 통하여 이제 정적분의 계산을 쉽게 할 수 있다. 정적분 계산할 때 부정적분이 사용되므로 이제까지 부정적분 구하는 연습을 한 것이다. 이 정리가 없었으면 정적분값을 구할 때, 항상 구분구적법 처음 할 때처럼, 구간을 나누고 도형의 합을 계산하고 극한으로 보내는 작업을 해야 한다.
각주
- ↑ 더 잘 설명된 그림이 있으면 추가바랍니다.
- ↑ 적당한 함수를 u(x)로 놓은 다음에 y를 u에 대해 미분한 함수*u를 x에 대해 미분한 함수 하면 된다.
- ↑ [math]\displaystyle{ \color{#996D9}{\sec x} }[/math]는 [math]\displaystyle{ \color{#996D9}{\frac{1}{\cos x}} }[/math]입니다.
- ↑ [math]\displaystyle{ \color{#952D9}{\csc x} }[/math]는 [math]\displaystyle{ \color{#952D9}{\frac{1}{\sin x}} }[/math]입니다.
- ↑ [math]\displaystyle{ \color{#99D9}{\cot x} }[/math]는 [math]\displaystyle{ \color{#99D9}{\frac{1}{\tan x}} }[/math]입니다.
- ↑ 단 [math]\displaystyle{ \color{#520FF}{x=g(t)} }[/math].
- ↑ [math]\displaystyle{ \color{#0059FF}{\arccos x} }[/math]은 [math]\displaystyle{ \color{#037FF}{\cos x} }[/math]의 역함수입니다.
- ↑ [math]\displaystyle{ \color{#0059FF}{\cos x} }[/math]의 정의역을 [math]\displaystyle{ \color{#0059FF}{0\leq x \leq \pi } }[/math] 로 제한하면 [math]\displaystyle{ \color{#0059FF}{\cos x} }[/math]도 역함수를 갖게 된다.이때 역함수의 경우에는 정의역이 원함수의 치역이고 치역이 원함수의 정의역이다.
- ↑ 상수도 엄연히 다항함수입니다.
- ↑ a, b를 포함하는 구간을 닫힌 구간이라고 합니다. 이상과 이하의 개념으로 이해하시면 될 것 같습니다. a이상 b이하
- ↑ 기본 도형은 직사격형, 이등변삼각형, 원기둥, 직육면체등과 같이 넓이 또는 부피를 쉽게 구할 수 있는 도형으로 정해야 합니다.
- ↑ 보통 여기서 Σ(시그마)와 k, k^2, k^3의 공식이 사용됩니다.
| 쉽게 알 수 있는 학문 | |
|---|---|
| 쉽게 할 수 있는 취미 | |
| 창작 안내서 시리즈 | |
| 뭘헤매지 시리즈 | |
| 여행 시리즈 | |
| 연표 시리즈 | |
| 생활의 지혜 | |
| 리브레 기네스 | |
| 리브레 위키 | |
| 기타 | |