(→정적분: 말투를 고치고 기타 등등) |
|||
| 3번째 줄: | 3번째 줄: | ||
|수포자도 쉽게 알 수 있는 수학/질문|도와주세요! 리브레 수학 선생님! 코너 바로가기}} | |수포자도 쉽게 알 수 있는 수학/질문|도와주세요! 리브레 수학 선생님! 코너 바로가기}} | ||
{{:수포자도 쉽게 알 수 있는 수학}} | {{:수포자도 쉽게 알 수 있는 수학}} | ||
이 문서에는 극한 개념이 포함되어 있습니다. 극한에 대해 알고 싶은 분은 [[수포자도 쉽게 알 수 있는 수학/함수#극한|쉬운 수학:극한]]을 참고하세요. | |||
=== [[미분]] === | === [[미분]] === | ||
<s>고등학생들에겐 악몽의 시작</s> | |||
미분은 간단히 말하면 어떤 함수의 도함수를 구하는 과정이다. <s>도함수는 뭔데요?</s> <s>[[순환논증|도함수는 함수를 미분했을 때 나오는 함수이다.]]</s> | |||
==== 미분의 시작, 변화율 ==== | |||
어떤 자동차가 0m의 출발선에서 출발한 뒤 점점 가속도를 붙여 1초 후에 1m, 2초 후에 4m, 3초 후에 9m … 에 도달한다고 해 보자. 즉 자동차는 갈수록 빨라져서 <math>x</math>초 후 자동차의 위치는 <math>x^2</math>m가 된다. <s>2시간 후에는 지구를 한바퀴 돈다</s> 그러면 10초 후에는 100m를 갔을 것이고, 10초 동안의 속력을 계산해 보면 속력은 거리/시간 이니까 100m / 10초 = 10m/s 가 된다. | |||
그런데 이건 '10초 동안의 평균 속력' 이지, '10초가 된 순간에 자동차 계기판에 찍힌 순간 속력'은 아니다. 그렇다면 정확히 10초가 된 순간의 속력을 구하기 위해서는 어떻게 해야 할까? | |||
10초가 된 '순간'이라는 것은 10초 근처에서의 '아주 짧은 시간' 동안이라는 것이다. 그러니까 9.999초와 10초 사이의 속력, 혹은 10초와 10.001초 사이의 속력은 10초에서의 순간속력과 거의 비슷하다. 오차를 더 줄이고 싶다면 9.999… 뒤로 9를 더 많이 붙이면 될 것이다. | |||
수식으로 생각해보자. 9초일 때 자동차의 위치는 81m, 9.9초일 때는 98.01m, 9.99초일 때는 99.8001m, … 이다. 그러면 자동차의 속력은 <math>\frac{100m - 81m}{10초 - 9초}, \frac{100m - 98.01m}{10초 - 9.9초}, \frac{100m - 99.8001m}{10초 - 9.99초}</math> … 가 될 것이다. | |||
9를 무한히 붙여나갈 때 속력은 극한을 사용해서<math>\lim_{x \rightarrow 10}\frac{100 - x^2}{10 - x}</math>라고 쓸 수 있고, 인수분해해서 계산하면 <math>\lim_{x \rightarrow 10}\frac{100 - x^2}{10 - x} = \lim_{x \rightarrow 10}\frac{(10 + x)(10 - x)}{10 - x} = \lim_{x \rightarrow 10}(10 + x) = 20 </math> | |||
즉 10초가 된 순간의 자동차의 속력이 20m/s 임을 함수의 극한을 이용해 구한 것이다. | |||
[[File:Derivative GIF.gif|thumb|미분의 원리를 보여 주는 움짤. 두 점 사이의 평균변화율을 나타내는 직선이, 두 점이 한없이 가까워지면 한 점의 순간변화율로 수렴한다.<ref>더 잘 설명된 그림이 있으면 추가바랍니다.</ref>]] | |||
이걸 | 이걸 좀 더 일반화해서, 10초일 때가 아니라 시간 <math>x</math>초에서의 속력을 구하려고 한다. 시간이 <math>x</math>초일 때 자동차가 간 거리는 <math>x^2</math>이다. 그리고 <math>x</math> 보다 약간 작은 <math>x-h</math> 초일 때를 생각해 보면, <math>x-h</math> 초일 때의 거리는 <math>(x-h)^2</math> 가 될 것이고, 위에서 한 것처럼 순간 속력은 <math>h</math>가 0에 가까워져 <math>x</math>와 <math>x-h</math> 가 아주 가까워질 때를 생각하면 된다. | ||
<math>\lim_{h \rightarrow 0}\frac{x^2 - (x - h)^2}{x - (x - h)} = \lim_{h \rightarrow 0}\frac{x^2 - x^2 + 2hx - h^2}{h} = \lim_{h \rightarrow 0}(2x - h) = 2x </math> | <math>\lim_{h \rightarrow 0}\frac{x^2 - (x - h)^2}{x - (x - h)} = \lim_{h \rightarrow 0}\frac{x^2 - x^2 + 2hx - h^2}{h} = \lim_{h \rightarrow 0}(2x - h) = 2x </math> | ||
따라서 x 초가 된 순간의 자동차의 속력은 2x m/s이다. 매번 9, 9.9, 9.99 | 따라서 <math>x</math>초가 된 순간의 자동차의 속력은 <math>2x</math>m/s이다. 매번 9, 9.9, 9.99 … 의 제곱을 구해서 100에서 빼고 나누고 하는 귀찮은 짓을 할 필요 없이, 이제 10초일 때의 속력은 20, 20초일 때는 40... 이렇게 바로 구할 수 있게 된 것이다! 이게 바로 ''' '함수를 미분'''' 한 것이다. <s>드디어 미분을 정의했다!</s> | ||
==== 그래서, 미분을 왜 쓰는데? ==== | |||
미분이라는 것은 어떤 함수 <math>f(x)</math>가 있을 때 <math>(x, f(x))</math>에서 <math>f(x)</math>와 접하는 선, 즉 접선의 기울기를 구할 때에 사용된다. | 미분이라는 것은 어떤 함수 <math>f(x)</math>가 있을 때 <math>(x, f(x))</math>에서 <math>f(x)</math>와 접하는 선, 즉 접선의 기울기를 구할 때에 사용된다. | ||
| 44번째 줄: | 51번째 줄: | ||
==== 상수함수의 미분법 ==== | ==== 상수함수의 미분법 ==== | ||
[[File:Constant function.png| | [[File:Constant function.png|140픽셀|thumb|상수함수의 그래프]] | ||
상수함수란 x의 값에 상관없이 항상 함숫값이 | 상수함수란 x의 값에 상관없이 항상 함숫값이 일정한 함수다. 즉 <math>f(x)=c</math><ref>상수(Constant)의 첫글자 c를 따서, '일정한 값'인 상수를 표시할 때는 c를 많이 쓴다.</ref>인 함수가 있을 때, 도함수 <math>f'(x)=0</math>이다. | ||
미분계수가 그래프에서의 기울기를 뜻하므로, 직관적으로도 도함수는 항상 0임을 알 수 있다. | 미분계수가 그래프에서의 기울기를 뜻하므로, 직관적으로도 도함수는 항상 0임을 알 수 있다. | ||
2015년 6월 10일 (수) 00:08 판
이 문서에는 극한 개념이 포함되어 있습니다. 극한에 대해 알고 싶은 분은 쉬운 수학:극한을 참고하세요.
미분
고등학생들에겐 악몽의 시작
미분은 간단히 말하면 어떤 함수의 도함수를 구하는 과정이다. 도함수는 뭔데요? 도함수는 함수를 미분했을 때 나오는 함수이다.
미분의 시작, 변화율
어떤 자동차가 0m의 출발선에서 출발한 뒤 점점 가속도를 붙여 1초 후에 1m, 2초 후에 4m, 3초 후에 9m … 에 도달한다고 해 보자. 즉 자동차는 갈수록 빨라져서 [math]\displaystyle{ x }[/math]초 후 자동차의 위치는 [math]\displaystyle{ x^2 }[/math]m가 된다. 2시간 후에는 지구를 한바퀴 돈다 그러면 10초 후에는 100m를 갔을 것이고, 10초 동안의 속력을 계산해 보면 속력은 거리/시간 이니까 100m / 10초 = 10m/s 가 된다.
그런데 이건 '10초 동안의 평균 속력' 이지, '10초가 된 순간에 자동차 계기판에 찍힌 순간 속력'은 아니다. 그렇다면 정확히 10초가 된 순간의 속력을 구하기 위해서는 어떻게 해야 할까?
10초가 된 '순간'이라는 것은 10초 근처에서의 '아주 짧은 시간' 동안이라는 것이다. 그러니까 9.999초와 10초 사이의 속력, 혹은 10초와 10.001초 사이의 속력은 10초에서의 순간속력과 거의 비슷하다. 오차를 더 줄이고 싶다면 9.999… 뒤로 9를 더 많이 붙이면 될 것이다.
수식으로 생각해보자. 9초일 때 자동차의 위치는 81m, 9.9초일 때는 98.01m, 9.99초일 때는 99.8001m, … 이다. 그러면 자동차의 속력은 [math]\displaystyle{ \frac{100m - 81m}{10초 - 9초}, \frac{100m - 98.01m}{10초 - 9.9초}, \frac{100m - 99.8001m}{10초 - 9.99초} }[/math] … 가 될 것이다. 9를 무한히 붙여나갈 때 속력은 극한을 사용해서[math]\displaystyle{ \lim_{x \rightarrow 10}\frac{100 - x^2}{10 - x} }[/math]라고 쓸 수 있고, 인수분해해서 계산하면 [math]\displaystyle{ \lim_{x \rightarrow 10}\frac{100 - x^2}{10 - x} = \lim_{x \rightarrow 10}\frac{(10 + x)(10 - x)}{10 - x} = \lim_{x \rightarrow 10}(10 + x) = 20 }[/math]
즉 10초가 된 순간의 자동차의 속력이 20m/s 임을 함수의 극한을 이용해 구한 것이다.

이걸 좀 더 일반화해서, 10초일 때가 아니라 시간 [math]\displaystyle{ x }[/math]초에서의 속력을 구하려고 한다. 시간이 [math]\displaystyle{ x }[/math]초일 때 자동차가 간 거리는 [math]\displaystyle{ x^2 }[/math]이다. 그리고 [math]\displaystyle{ x }[/math] 보다 약간 작은 [math]\displaystyle{ x-h }[/math] 초일 때를 생각해 보면, [math]\displaystyle{ x-h }[/math] 초일 때의 거리는 [math]\displaystyle{ (x-h)^2 }[/math] 가 될 것이고, 위에서 한 것처럼 순간 속력은 [math]\displaystyle{ h }[/math]가 0에 가까워져 [math]\displaystyle{ x }[/math]와 [math]\displaystyle{ x-h }[/math] 가 아주 가까워질 때를 생각하면 된다.
[math]\displaystyle{ \lim_{h \rightarrow 0}\frac{x^2 - (x - h)^2}{x - (x - h)} = \lim_{h \rightarrow 0}\frac{x^2 - x^2 + 2hx - h^2}{h} = \lim_{h \rightarrow 0}(2x - h) = 2x }[/math]
따라서 [math]\displaystyle{ x }[/math]초가 된 순간의 자동차의 속력은 [math]\displaystyle{ 2x }[/math]m/s이다. 매번 9, 9.9, 9.99 … 의 제곱을 구해서 100에서 빼고 나누고 하는 귀찮은 짓을 할 필요 없이, 이제 10초일 때의 속력은 20, 20초일 때는 40... 이렇게 바로 구할 수 있게 된 것이다! 이게 바로 '함수를 미분' 한 것이다. 드디어 미분을 정의했다!
그래서, 미분을 왜 쓰는데?
미분이라는 것은 어떤 함수 [math]\displaystyle{ f(x) }[/math]가 있을 때 [math]\displaystyle{ (x, f(x)) }[/math]에서 [math]\displaystyle{ f(x) }[/math]와 접하는 선, 즉 접선의 기울기를 구할 때에 사용된다.
이를 어떻게 구하는지 보자. [math]\displaystyle{ f(x) }[/math] 함수 위의 두 점, [math]\displaystyle{ (a, f(a)) }[/math]와 [math]\displaystyle{ (b, f(b)) }[/math]를 지나는 선의 기울기는 다음과 같을 것이다.
기울기 : [math]\displaystyle{ \frac{f(b) - f(a)}{b-a} }[/math]
이를 그대로 적용해서, 점 [math]\displaystyle{ (x, f(x)) }[/math]와 그로부터 x축으로 [math]\displaystyle{ \Delta x }[/math]만큼 떨어진 [math]\displaystyle{ (x+\Delta x, f(x+\Delta x)) }[/math] 의 기울기를 표현하면 다음과 같을 것이다.
기울기 : [math]\displaystyle{ \frac{f(x+\Delta x) - f(x)}{ (x + \Delta x) - x} = \frac{f(x+\Delta x) - f(x)}{ \Delta x} }[/math]
이 때 [math]\displaystyle{ \Delta x }[/math]가 작아질수록 이 두 점을 연결하는 선은 점점 우리가 구하고자 하는 접선의 기울기에 가까워지게 된다. 따라서, 함수 [math]\displaystyle{ f(x) }[/math]의 접선의 기울기는 다음과 같이 표현할 수 있다.
접선의 기울기 : [math]\displaystyle{ \lim_{\Delta x\rightarrow 0}\frac{f(x+\Delta x) - f(x)}{ \Delta x} }[/math]
이를 함수 [math]\displaystyle{ f(x) }[/math]의 도함수라고 하며, [math]\displaystyle{ f'(x) }[/math] 또는 [math]\displaystyle{ \frac {\mathrm dy}{\mathrm dx} }[/math]라고 표기한다. 전자는 함수 [math]\displaystyle{ f(x) }[/math]의 도함수라는 것을 표현한 것이며, 후자는 접선의 기울기를 나타낸다는 것을 표현한 것이다. 문제에 따라서 편리한 표현방법을 사용하게 된다.
상수함수의 미분법
상수함수란 x의 값에 상관없이 항상 함숫값이 일정한 함수다. 즉 [math]\displaystyle{ f(x)=c }[/math][2]인 함수가 있을 때, 도함수 [math]\displaystyle{ f'(x)=0 }[/math]이다.
미분계수가 그래프에서의 기울기를 뜻하므로, 직관적으로도 도함수는 항상 0임을 알 수 있다.
다항함수의 미분법
다항함수의 미분법은 아주 간단하다. 빼기, 곱하기만 할 수 있으면 누구나 할 수 있다. 물론 그 증명도 중요하지만 일단 계산법만 올려보자면 아래와 같다.
실수 n에 대해 함수 [math]\displaystyle{ {x}^{n} }[/math]의 도함수는 다음과 같다.
[math]\displaystyle{ ({x}^{n})'=n{x}^{n-1} }[/math].
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}({x}^{n})=n{x}^{n-1} }[/math]
n이 자연수일 때의 증명
다음과 같은 계산 과정을 통해서 자연수에 대해서 증명이 가능하고, 미분에 대한 지식 몇 가지만 추가하면 실수 n에 대해서 확장할 수 있다. 그러나 어렵다 싶으면 일단 그냥 암기해서 이용해도 문제없는 부분이다.
[math]\displaystyle{ \lim_{\Delta x\to 0} \frac{(x+\Delta x)^n - x^n}{\Delta x} = \lim_{\Delta x\rightarrow 0} \frac{nx^{n-1}\Delta x+\frac{n(n-1)}{2} x^{n-2}\Delta x^2 + ... + nx\Delta x^{n-1} + \Delta x^n }{\Delta x} }[/math]
[math]\displaystyle{ = \lim_{\Delta x \to 0} \left( nx^{n-1} + \frac{n(n-1)}{2} x^{n-2}\Delta x + ... + nx\Delta x^{n-1} + \Delta x^{n-1} \right) = nx^{n-1} }[/math]
[math]\displaystyle{ \Delta x }[/math]를 약분하고 [math]\displaystyle{ \Delta x }[/math]의 1차항 이상은 극한이 0으로 가므로 무시할 수 있어서, 위 함수의 도함수는 [math]\displaystyle{ n{x}^{n-1} }[/math]이 된다. 이것을 미분에 있어서의 Power Rule, 지수법칙이라고 부른다.
상수배
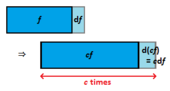
[math]\displaystyle{ (cf(x))'=c(f(x))' }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}(cf(x))=c\frac{\mathrm d}{\mathrm dx}(f(x)) }[/math]
증명
[math]\displaystyle{ \left( cf(x) \right)' = \lim_{h \to 0} \frac{cf(x+h)-cf(x)}{h} = \lim_{h \to 0} c\;\frac{f(x+h)-f(x)}{h} = cf'(x) }[/math]
그림에서 [math]\displaystyle{ \mathrm d(cf) = c\mathrm df }[/math]임을 알 수 있고, 양변을 [math]\displaystyle{ \mathrm dx }[/math]로 나눠 주면 [math]\displaystyle{ \frac{\mathrm d(cf)}{\mathrm dx} = c \frac{\mathrm df}{\mathrm dx} }[/math]가 되어 원하는 결과를 얻는다.
합차
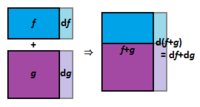
[math]\displaystyle{ (f(x) \pm g(x))'=f'(x) \pm g'(x) }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}(f(x) \pm g(x))=\frac{\mathrm d}{\mathrm dx}(f(x)) \pm \frac{\mathrm d}{\mathrm dx}(g(x)) }[/math]
증명
[math]\displaystyle{ (f(x) \pm g(x))' = \lim_{h \to 0} \frac{(f(x+h) \pm g(x+h))-(f(x) \pm g(x))}{h} }[/math]
[math]\displaystyle{ = \lim_{h \to 0} \left( \frac{f(x+h)-f(x)}{h} \pm \frac{g(x+h)-g(x)}{h} \right) = f'(x) \pm g'(x) }[/math]
그림에서 [math]\displaystyle{ \mathrm d(f+g) = \mathrm df+\mathrm dg }[/math]임을 알 수 있고, 양변을 [math]\displaystyle{ \mathrm dx }[/math]로 나눠 주면 [math]\displaystyle{ \frac{\mathrm d(f+g)}{\mathrm dx} = \frac{\mathrm df}{\mathrm dx} + \frac{\mathrm dg}{\mathrm dx} }[/math]가 되어 원하는 결과를 얻는다.
곱
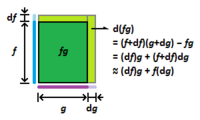
[math]\displaystyle{ (f(x)g(x))'=f'(x)g(x)+f(x)g'(x) }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}(f(x)g(x))=\frac{\mathrm d}{\mathrm dx}(f(x))g(x)+f(x)\frac{\mathrm d}{\mathrm dx}(g(x)) }[/math]
증명
[math]\displaystyle{ (f(x)g(x))' = \lim_{h \to 0} \frac{f(x+h)g(x+h)-f(x)g(x)}{h} = \lim_{h \to 0} \frac{f(x+h)g(x+h)-f(x)g(x+h)+f(x)g(x+h)-f(x)g(x)}{h} }[/math]
그림에서 [math]\displaystyle{ \mathrm d(fg) = (\mathrm df)g+f(\mathrm dg) }[/math]임을 알 수 있고, 양변을 [math]\displaystyle{ \mathrm dx }[/math]로 나눠 주면 [math]\displaystyle{ \frac{\mathrm d(fg)}{\mathrm dx} = \frac{\mathrm df}{\mathrm dx} g + f \frac{\mathrm dg}{\mathrm dx} }[/math]가 되어 원하는 결과를 얻는다.
왜 [math]\displaystyle{ \mathrm df\mathrm dg }[/math]를 무시해도 되는지는 좀 설명이 필요하다. [math]\displaystyle{ \mathrm df }[/math]와 [math]\displaystyle{ \mathrm dg }[/math] 모두 [math]\displaystyle{ \mathrm dx }[/math]가 줄어듦에 따라 같이 줄어든다. 따라서 [math]\displaystyle{ \mathrm df\mathrm dg }[/math]는 [math]\displaystyle{ \mathrm df }[/math]가 줄어드는 속도와 [math]\displaystyle{ \mathrm dg }[/math]가 줄어드는 속도의 영향을 중첩적으로 받아 훨씬 빨리 줄어들게 된다. 즉 [math]\displaystyle{ \mathrm df\mathrm dg }[/math]가 줄어드는 속도가 [math]\displaystyle{ \mathrm dx }[/math]가 줄어드는 속도보다 한층 빠르고, 따라서 무시해도 되는 것이다. 즉 [math]\displaystyle{ \mathrm df\mathrm dg }[/math]가 작아서 무시한다는 말은 좀 그렇고, 작긴 작은데 그 정도가 [math]\displaystyle{ \mathrm dx }[/math]보다 한층 더하기 때문에 무시해도 된다는 것이다.
합성함수
[math]\displaystyle{ y=f(u) }[/math], [math]\displaystyle{ u=g(x) }[/math]이고 둘 다 미분가능하면
[math]\displaystyle{ (f(g(x)))'=f'(g(x)) g'(x) }[/math]
[math]\displaystyle{ \frac{\mathrm dy}{\mathrm dx}=\frac{\mathrm dy}{\mathrm du}\times \frac{\mathrm du}{\mathrm dx} }[/math][3]
증명
[math]\displaystyle{ (f(g(x)))' = \lim_{h \to 0} \frac{f(g(x+h))-f(g(x))}{h} = \lim_{h \to 0} \left( \frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x)} \; \frac{g(x+h)-g(x)}{h} \right) }[/math]
이 때 [math]\displaystyle{ h \rightarrow 0 }[/math]이면 [math]\displaystyle{ g(x+h) \rightarrow g(x) }[/math]이므로
[math]\displaystyle{ (f(g(x)))' = \lim_{g(x+h) \to g(x)} \frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x)} × \lim_{h \to 0} \frac{g(x+h)-g(x)}{h} = f'(g(x))g'(x) }[/math]
삼각함수
- 삼각함수 공식 외우기는 삼각함수 공식을 외워보자 참고.
사인
[math]\displaystyle{ (\sin x)'=\cos x }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}(\sin x)=\cos x }[/math]
[math]\displaystyle{ (\cos x)'=-\sin x }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}(\cos x)=-\sin x }[/math]
[math]\displaystyle{ \color{asd} (\tan x)'={\sec }^{2} x }[/math]
[math]\displaystyle{ {\frac{\mathrm d}{\mathrm dx}(\tan x)={\sec }^{2} x} }[/math]
역함수
임의의 함수 [math]\displaystyle{ f(x) }[/math]의 역함수
[math]\displaystyle{ {{f}^{-1}(x)} }[/math] 가 존재하면.
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}({f}^{-1}(x))=\frac{1}{f'({f}^{-1}(x))} }[/math].
지수함수
[math]\displaystyle{ \color{#5140F2}{ (e^x)' = e^x} }[/math]
[math]\displaystyle{ \color{#5140F2}{ (a^x)' = a^x \ln a} }[/math]
[math]\displaystyle{ \color{#5140F2}{ \frac{\mathrm d}{\mathrm dx}e^x = e^x} }[/math]
[math]\displaystyle{ \color{#5140F2}{\frac{\mathrm d}{\mathrm dx}({a}^{x})={a}^{x}\ln a} }[/math].
[math]\displaystyle{ \color{#5140F2}{a\neq 1,a\gt 0} }[/math].
로그함수
[math]\displaystyle{ (\ln x)' = \frac{1}{x} }[/math]
[math]\displaystyle{ (\log_{a} x)' = \frac{1}{x \ln a} }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx}\ln x = \frac{1}{x} }[/math]
[math]\displaystyle{ \frac{\mathrm d}{\mathrm dx} \log_{a} x = \frac{1}{x \ln {a}} }[/math]
평균값 정리
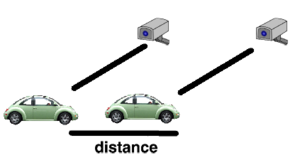
도로교통 이야기로 잠시 넘어가보자. 구간단속은 일정 구간에서 평균 속도가 제한 속도를 위반하면 적발하는 단속 방법이다. 이전까지 쓰이던 지점단속에는 단속 대상자가 카메라 앞에서만 속도를 잠시 줄인 뒤 카메라에서 벗어나면 다시 과속을 할 수 있다는 문제가 있었다. 그러나 구간단속에서는 이런 꼼수가 원천 차단된다.
예를 들어 어떤 운전자의 차량이 적발 속도가 80km/h이고 길이가 1km인 구간단속 시작지점에 들어설 때 시속 60km으로 달리고 있었다고 가정하고 30초 후 끝지점으로 나올 때 여전히 시속 60km로 달리고 있었다고 가정하자. 이때 이 차량의 평균 속도는 120km/h이다. 이 결과는 단속구간에 있을 때 어느 순간 차량의 순간속도가 120km/h을 찍었다는 걸 의미한다. 지점단속으로는 단속에 걸리지 않지만 구간단속으로는 얄짤없이 단속에 걸리게 된다. 이 상황을 약간 추상화하면, 어느 구간에서 (구간 양끝 함수값의 차)/(구간 양끝점의 차)의 값과 같은 미분계수를 가지는 지점이 존재한다는 결론을 얻고, 이것이 바로 평균값 정리다. 물론 아무 때나 쓰면 곤란하고 평균값 정리가 성립하기 위한 조건들이 있으니, 더 자세히 알고 싶으면 항목을 참조하길.
적분
부정적분
문과생에게도 잘 알려져 있는 "적분은 미분 거꾸로, 미분은 적분 거꾸로"
상수배
[math]\displaystyle{ \color{#177636}{\int cf(x) dx=c\int f(x) dx} }[/math]
합차
[math]\displaystyle{ \color{#EE497F}{\int (f(x)\pm g(x)) dx=\int f(x) dx\pm\int g(x) dx} }[/math]
[math]\displaystyle{ \color{#FF00}{{x}^{n}} }[/math]
| 함수 | 역도함수(부정적분) | ||
|---|---|---|---|
| [math]\displaystyle{ \color{#FF00}{{x}^{n}} }[/math] | [math]\displaystyle{ \color{#FF00}{n \neq -1} }[/math] | [math]\displaystyle{ \color{#AC0FF}{\frac{{x}^{n+1}}{n+1}+C} }[/math] | |
| [math]\displaystyle{ \color{#FF00}{n = -1} }[/math] | [math]\displaystyle{ \color{#591759}{\ln |x|+C} }[/math] | ||
삼각함수
| 함수 | 역도함수(부정적분) | |
|---|---|---|
| [math]\displaystyle{ \color{#0ACFF}{\sin x} }[/math] | [math]\displaystyle{ \color{#156B94}{-\cos x +C} }[/math] | |
| [math]\displaystyle{ \color{#9D99}{\cos x} }[/math] | [math]\displaystyle{ \color{#9D9D9}{\sin x+C} }[/math] | |
| [math]\displaystyle{ \color{#996D9}{{\sec}^{2} x} }[/math][4] | [math]\displaystyle{ \color{#9D99}{\tan x+C} }[/math] | |
| [math]\displaystyle{ \color{#952D9}{{\csc}^{2} x} }[/math][5] | [math]\displaystyle{ \color{#99D9}{-\cot x+C} }[/math][6] | |
| [math]\displaystyle{ \color{#FF69AC}{\sec x \tan x} }[/math] | [math]\displaystyle{ \color{#FF69AC}{\sec x +C} }[/math] | |
| [math]\displaystyle{ \color{#059FF}{\csc x \cot x} }[/math] | [math]\displaystyle{ \color{#01952}{-\csc x +C} }[/math] | |
[math]\displaystyle{ \color{#173876}{{a}^{x},a\gt 0,a\neq 1} }[/math]
[math]\displaystyle{ \color{#B5107F}{\int {a}^{x} dx=\frac{{a}^{x}}{\ln a}+C} }[/math]
치환적분법
[math]\displaystyle{ \color{#177617}{\int f(x) dx=\int f(g(t))g'(t) dt} }[/math][7]
뭐 이렇기는 한데,미분의 합성함수의 미분법과는 달리 치환적분법은 모든 합성함수에 대해 적용할 수가 없다.
오히려 적용이 거의 안되는 함수가 훨씬 더 많다.
음 전혀 간단하지 않게 말하자면 [math]\displaystyle{ \color{#177617}{t} }[/math]=(
[math]\displaystyle{ \color{#177617}{x} }[/math]에 관한 적당한 함수)로 놓고
[math]\displaystyle{ \color{#177617}{x} }[/math]=([math]\displaystyle{ \color{#177617}{t} }[/math]에 관한 함수)로 적절히 변형한 다음에 위 식에 대입하자.
예시 1
[math]\displaystyle{ \color{#0ACFF}{\int {(2x+1)}^{3} dx} }[/math]
[math]\displaystyle{ \color{#0ACFF}{2x+1=t,f(x)={(2x+1)}^{3}} }[/math]로 놓자.
양변에 1을 빼면.
[math]\displaystyle{ \color{#0ACFF}{2x=t-1=g(t)} }[/math]
이제 양변을 2로 나누자.
[math]\displaystyle{ \color{#0ACFF}{x=\frac{t-1}{2}=g(t)} }[/math]
[math]\displaystyle{ \color{#0ACFF}{g'(t)=\frac{1}{2}=\frac{dx}{dt}} }[/math]
이제 [math]\displaystyle{ \color{#0ACFF}{f(x)} }[/math] 에 대입하면.
[math]\displaystyle{ \color{#0ACFF}{\int {((2\times \frac{t-1}{2} +1)}^{3}\times \frac{1}{2}) dt} }[/math]
[math]\displaystyle{ \color{#0ACFF}{\int \frac{1}{2}{t}^{3} dt} }[/math]
상수는 밖으로 빼내자.
[math]\displaystyle{ \color{#0ACFF}{\frac{1}{2} \int {t}^{3} dt} }[/math]
[math]\displaystyle{ \color{#0ACFF}{\frac{1}{2}\times \frac{1}{4}{t}^{4}+C} }[/math]
[math]\displaystyle{ \color{#0ACFF}{\frac{1}{8}{t}^{4}+C} }[/math]
[math]\displaystyle{ \color{#0ACFF}{t=2x+1} }[/math]이므로 [math]\displaystyle{ \color{#0ACFF}{t} }[/math]에 대입하자.
[math]\displaystyle{ \color{#0ACFF}{\frac{1}{8}{(2x+1)}^{4}+C} }[/math]
예시 2
[math]\displaystyle{ \color{#0059FF}{\int \tan x dx} }[/math]
[math]\displaystyle{ \color{#0059FF}{\int \frac{\sin x}{\cos x} dx} }[/math]
[math]\displaystyle{ \color{#0059FF}{\cos x=t,f(x)=\frac{\sin x}{\cos x}} }[/math]로 둡니다.
[math]\displaystyle{ \color{#0059FF}{x=g(t)} }[/math]꼴로 만들기 위해서 양변에
[math]\displaystyle{ \color{#0059FF}{\arccos x} }[/math][8]를 취합니다.
[math]\displaystyle{ \color{#0059FF}{\arccos t=x=g(t)} }[/math]
이제 [math]\displaystyle{ \color{#0059FF}{g'(t)=\frac{dx}{dt}} }[/math]를 구해봅시다.
수포자도 쉽게 알 수 있는 수학#역함수에서 [math]\displaystyle{ \color{#037FF}{f(x)=\cos x,f'(x)=-\sin x} }[/math]가 가 된다.
그러면 [math]\displaystyle{ \color{#0059FF}{\frac{d}{dx}(\arccos x)=\frac{1}{-\sin (\arccos x)}} }[/math]이 됩니다.
[math]\displaystyle{ \color{#0059FF}{\frac{d}{dx}(\arccos x)=\frac{1}{-\sin (\arccos x)}} }[/math]
[math]\displaystyle{ \color{#0059FF}{{\sin}^{2} (\arccos x)+{\cos}^{2} (\arccos x)=1} }[/math]
[math]\displaystyle{ \color{#0059FF}{{\sin}^{2} (\arccos x)+{x}^{2}=1} }[/math]
[math]\displaystyle{ \color{#0059FF}{{\sin}^{2} (\arccos x)=1-{x}^{2}} }[/math]
[math]\displaystyle{ \color{#0059FF}{{\sin} (\arccos x)=\pm \sqrt{1-{x}^{2}}} }[/math]
그런데 [math]\displaystyle{ \color{#0059FF}{0\leq \arccos x\leq \pi } }[/math]
[9]
이고 [math]\displaystyle{ \color{#0059FF}{0\leq \ x \leq \pi } }[/math]에서
[math]\displaystyle{ \color{#0059FF}{\sin x\geq 0} }[/math]이다.
따라서 [math]\displaystyle{ \color{#0059FF}{\sin (\arccos x)=\sqrt{1-{x}^{2}}} }[/math]이다.
따라서 [math]\displaystyle{ \color{#0059FF}{g'(t)=\frac{1}{-\sqrt{1-{t}^{2}}}} }[/math]입니다.
대입하면.
[math]\displaystyle{ \color{#0059FF}{\int \frac{-\sin (\arccos t)}{\cos (\arccos t)\times \sqrt{1-{t}^{2}}} dt} }[/math]
[math]\displaystyle{ \color{#0059FF}{\int \frac{-\sqrt{1-{t}^{2}}}{t\times \sqrt{1-{t}^{2}}} dt} }[/math]
[math]\displaystyle{ \color{#0059FF}{\int \frac{-1}{t} dt} }[/math]
[math]\displaystyle{ \color{#0059FF}{-\int \frac{1}{t} dt} }[/math]
[math]\displaystyle{ \color{#0059FF}{-\ln |t| +C} }[/math]
[math]\displaystyle{ \color{#0059FF}{t=\cos x} }[/math]이므로 대입합니다.
[math]\displaystyle{ \color{#0059FF}{-\ln |\cos x| +C} }[/math]
부분적분법
[math]\displaystyle{ \color{#C06AE9}{\int f(x)g'(x) dx=f(x)g(x)-\int f'(x)g(x)dx} }[/math]
로그함수,역삼각함수,다항함수,삼각함수,지수함수 중에서 가장 먼저의 것을
[math]\displaystyle{ \color{#C06AE9}{f(x)} }[/math]에 대입하고 나머지를
[math]\displaystyle{ \color{#C06AE9}{g'(x)} }[/math]에 대입하는 것이 좋다.
곱의 미분법 적분판이라고 볼 수 있...지만 만능은 전혀 아니다.
예시 1
[math]\displaystyle{ \color{#C06AE9}{\int x{e}^{x} dx} }[/math]
일단 다항함수인 [math]\displaystyle{ \color{#C06AE9}{x} }[/math]를
[math]\displaystyle{ \color{#C06AE9}{f(x)} }[/math]에 대입하고 지수함수인
[math]\displaystyle{ \color{#C06AE9}{{e}^{x}} }[/math]를 [math]\displaystyle{ \color{#C06AE9}{g'(x)} }[/math]에 대입한다.
[math]\displaystyle{ \color{#C06AE9}{g'(x)={e}^{x},g(x)={e}^{x}+C} }[/math]
[math]\displaystyle{ \color{#C06AE9}{f(x)=x,f'(x)=1} }[/math]
이제 대입하면.
[math]\displaystyle{ \color{#C06AE9}{x({e}^{x}+C)-\int ((1\times ({e}^{x}+C)) dx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{x{e}^{x}+Cx-\int {e}^{x} dx-\int C dx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{x{e}^{x}+Cx-{e}^{x}+D-Cx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{Cx} }[/math]끼리 소거됩니다.
[math]\displaystyle{ \color{#C06AE9}{x{e}^{x}-{e}^{x}+D} }[/math]
적당히 인수분해합니다.D는 C는 둘다 적분상수이므로 D를 C로 바꾸어도 됩니다.
예시 2
[math]\displaystyle{ \color{#C06AE9}{\int \log_{a} x dx(a\gt 0)} }[/math]
먼저 로그함수인
[math]\displaystyle{ \color{#C06AE9}{\log_{a} x dx(a\gt 0)} }[/math]
를 [math]\displaystyle{ \color{#C06AE9}{f(x)} }[/math]에 대입한다.
그 다음에 다항함수인 1[10]을
[math]\displaystyle{ \color{#C06AE9}{g'(x)} }[/math]에 대입합니다.
자,이제 [math]\displaystyle{ \color{#C06AE9}{g(x)=x+C} }[/math]입니다.
[math]\displaystyle{ \color{#C06AE9}{\frac{1}{x \ln a}=f'(x)} }[/math]입니다.
이제 대입합니다.
[math]\displaystyle{ \color{#C06AE9}{\int {\log }_{a} x dx=(x+C)\log _{a}x-\int (\frac{1}{x \ln a}(x+C))dx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int \log _{a}x dx=(x+C)\log _{a}x-\int (\frac{1}{\ln a}+\frac{C}{x\ln a})dx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int \log _{a}x dx=(x+C)\log _{a}x-\int \frac{1}{\ln a} dx-\int \frac{C}{x\ln a}dx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int \log _{a}x dx=(x+C)\log _{a}x-\int \frac{1}{\ln a} dx-\frac{C}{\ln a}\int \frac{1}{x}dx} }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int \log _{a}x dx=(x+C)\log _{a}x-\frac{x}{\ln a} -\frac{C}{\ln a}
\ln |x|+D} }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int {\log}_{a} x dx=x {\log}_{a} x +C{\log}_{a} x-\frac{x}{\ln a}-\frac{C\ln |x|}{\ln a}+D} }[/math]
[math]\displaystyle{ \color{#C06AE9}{x\gt 0,|x|=x,{\log}_{a} x = \frac{{\ln}{x}}{\ln a} } }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int {\log}_{a} x dx=x {\log}_{a} x +C\frac{\ln x}{\ln a}-\frac{x}{\ln a}-\frac{C\ln x}{\ln a}+D } }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int {\log}_{a} x dx=x {\log}_{a} x +\frac{C\ln x}{\ln a}-\frac{x}{\ln a}-\frac{C\ln x}{\ln a}+D } }[/math]
[math]\displaystyle{ \color{#C06AE9}{\int {\log}_{a} x dx=x {\log}_{a} x -\frac{x}{\ln a}+D } }[/math]
[math]\displaystyle{ \color{#C06AE9}{D} }[/math]는 적분상수입니다.
끝입니다.
정적분
정적분이란 함수 y=f(x)와 닫힌 구간[a, b]로 둘러 싸인 도형의 넓이를 구하는 방법이다.[11] 사실 보통 배울 때 적분은 미분 거꾸로다... 라고 배우는데, 사실 미적분은 절대 같이 발달한 게 아니다. 단지 계산식이 그렇게 얽혀있을 뿐이다(미적분의 기본 정리인가 뭔가. 얼핏 보면 적분을 미분하면 원래 식이 나온다는 게 당연한 거 아닌가? 라는 생각도 들지만, 적분과 미분의 관계를 설명하는 중요한 포인트다. ). 여기서 미분과는 좀 상관없어 보이는 넓이 개념이 나오는 것도 그 때문.
구분구적법
도형의 넓이나 입체의 부피를 다음과 같이 구할 수 있다.
- 주어진 도형을 충분히 작은 여러 개의 기본 도형[12]으로 나누고,
- 그 기본 도형의 넓이 또는 부피의 합을 구할 수 있는 식을 만들고[13]
- 2에서 구한 식에서 n->∞일 때의 극한값을 구하면 됩니다.
이것이 바로 구분구적법이다.
다음은 구분 구적법을 적용해서 도형의 넓이를 구한 것이다.
화면 확대가 필요하다!도저히 작성자의 실력으로는 도형과 식들을 표현 할 수 없었다 카더라.
여기까지가 구분구적법의 설명! 하지만, 작성자가 구분구적법을 공부하실 위키러에게 드리고 싶은 말씀은, 수능에 안 나온다고, 중요하지 않다고 막 넘기시지 마시고, 어떻게 해서 구분구적법이 나오게 되었는가? 즉, 구분구적법의 원리와 발상을 공부해 보시라는 것이다. 위에서 말한 적분의 발생 기원과 관련있을지도...(단순한 미분 거꾸로가 아니라는 거)
정의
[math]\displaystyle{ \lim_{n\rightarrow \infty }\sum_{k=1}^{n}f(x_{k})\Delta x(\Delta x=\frac{b-a}{n},x_{k}=a+k\Delta x)=\int_{a}^{b}f(x)dx }[/math]
예제 1
[math]\displaystyle{ \int_{1}^{2} {x}^{2} dx }[/math]
[math]\displaystyle{ f(x)={x}^{2} }[/math]
[math]\displaystyle{ a=1,b=2,b-a=1 }[/math]
[math]\displaystyle{ \Delta x=\frac{1}{n},{x}_{k}=1+k\Delta x=1+\frac{k}{n} }[/math]
[math]\displaystyle{ \lim_{n\rightarrow \infty } \sum_{k=1}^{n}(1+\frac{k}{n})^2\frac{1}{n} }[/math]
[math]\displaystyle{ \lim_{n\rightarrow \infty } \sum_{k=1}^{n}(1+\frac{2k}{n}+\frac{k^{2}}{n^2})\frac{1}{n} }[/math]
[math]\displaystyle{ \lim_{n\rightarrow \infty } \sum_{k=1}^{n}(\frac{1}{n}+\frac{2k}{n^2}+\frac{k^{2}}{n^3}) }[/math]
[math]\displaystyle{ \lim_{n\rightarrow \infty }(\sum_{k=1}^{n}\frac{1}{n}+\sum_{k=1}^{n}\frac{2k}{n^2}+\sum_{k=1}^{n}\frac{{k}^{2}}{{n}^{3}}) }[/math]
[math]\displaystyle{ \lim_{n\rightarrow \infty }(\frac{1}{n}\sum_{k=1}^{n}1+\frac{2}{n^2}\sum_{k=1}^{n}k+\frac{1}{n^3}\sum_{k=1}^{n}{k}^{2}) }[/math]
그리고
[math]\displaystyle{ \sum_{k=1}^{n}k=\frac{n(n+1)}{2},\sum_{k=1}^{n}{k}^{2}=\frac{n(n+1)(2n+1)}{6} }[/math]
입니다.
[math]\displaystyle{ \lim_{n\rightarrow \infty }(1+\frac{2}{n^2}\frac{n(n+1)}{2}+\frac{1}{n^3}\frac{n(n+1)(2n+1)}{6}) }[/math]
[math]\displaystyle{ \lim_{n\rightarrow \infty }(1+\frac{n(n+1)}{n^2}+\frac{n(n+1)(2n+1)}{6n^3}) }[/math]
극한의 성질에 따라 세 식 모두 수렴하므로 각각 분리한다.
[math]\displaystyle{ \lim_{n\rightarrow \infty }1+\lim_{n\rightarrow \infty }\frac{n(n+1)}{n^2}+\lim_{n\rightarrow \infty }\frac{n(n+1)(2n+1)}{6n^3} }[/math]
[math]\displaystyle{ 1+1+\frac{1}{3}=\frac{7}{3} }[/math]
미적분의 기본정리
[math]\displaystyle{ f(x) }[/math]가 닫힌구간 [math]\displaystyle{ [a,b] }[/math]에서 연속일 때, [math]\displaystyle{ \frac{d}{dx} \int_{a}^{b} f(t)\, dt=f(x) }[/math]이다.
닫힌구간 [math]\displaystyle{ [a,b] }[/math]에서 연속인 함수 [math]\displaystyle{ f(x) }[/math]의 한 부정적분을 [math]\displaystyle{ F(x) }[/math]라고 할 때,
[math]\displaystyle{ \int_{a}^{b} f(x) dx=F(b)-F(a) }[/math]
이 미적분의 기본정리를 통하여 이제 정적분의 계산을 쉽게 할 수 있다. 정적분 계산할 때 부정적분이 사용되므로 이제까지 부정적분 구하는 연습을 한 것이다. 이 정리가 없었으면 정적분값을 구할 때, 항상 구분구적법 처음 할 때처럼, 구간을 나누고 도형의 합을 계산하고 극한으로 보내는 작업을 해야 한다.
각주
- ↑ 더 잘 설명된 그림이 있으면 추가바랍니다.
- ↑ 상수(Constant)의 첫글자 c를 따서, '일정한 값'인 상수를 표시할 때는 c를 많이 쓴다.
- ↑ 적당한 함수를 u(x)로 놓은 다음에 y를 u에 대해 미분한 함수*u를 x에 대해 미분한 함수 하면 된다.
- ↑ [math]\displaystyle{ \color{#996D9}{\sec x} }[/math]는 [math]\displaystyle{ \color{#996D9}{\frac{1}{\cos x}} }[/math]입니다.
- ↑ [math]\displaystyle{ \color{#952D9}{\csc x} }[/math]는 [math]\displaystyle{ \color{#952D9}{\frac{1}{\sin x}} }[/math]입니다.
- ↑ [math]\displaystyle{ \color{#99D9}{\cot x} }[/math]는 [math]\displaystyle{ \color{#99D9}{\frac{1}{\tan x}} }[/math]입니다.
- ↑ 단 [math]\displaystyle{ \color{#520FF}{x=g(t)} }[/math].
- ↑ [math]\displaystyle{ \color{#0059FF}{\arccos x} }[/math]은 [math]\displaystyle{ \color{#037FF}{\cos x} }[/math]의 역함수입니다.
- ↑ [math]\displaystyle{ \color{#0059FF}{\cos x} }[/math]의 정의역을 [math]\displaystyle{ \color{#0059FF}{0\leq x \leq \pi } }[/math] 로 제한하면 [math]\displaystyle{ \color{#0059FF}{\cos x} }[/math]도 역함수를 갖게 된다.이때 역함수의 경우에는 정의역이 원함수의 치역이고 치역이 원함수의 정의역이다.
- ↑ 상수도 엄연히 다항함수입니다.
- ↑ a, b를 포함하는 구간을 닫힌 구간이라고 합니다. 이상과 이하의 개념으로 이해하시면 될 것 같다. a이상 b이하
- ↑ 기본 도형은 직사격형, 이등변삼각형, 원기둥, 직육면체등과 같이 넓이 또는 부피를 쉽게 구할 수 있는 도형으로 정해야 한다.
- ↑ 보통 여기서 Σ(시그마)와 k, k^2, k^3의 공식이 사용다.
| 쉽게 알 수 있는 학문 | |
|---|---|
| 쉽게 할 수 있는 취미 | |
| 창작 안내서 시리즈 | |
| 뭘헤매지 시리즈 | |
| 여행 시리즈 | |
| 연표 시리즈 | |
| 생활의 지혜 | |
| 리브레 기네스 | |
| 리브레 위키 | |
| 기타 | |