부등식

부등식(不等式, Inequality)은 수학에서 두 수의 크기를 비교하는 식을 가리킨다.

개요

방정식이 [math]\displaystyle{ a=b }[/math]와 같이 어떤 두 정식의 같음을 비교하는 것이라면, 부등식은 같지 않음을 비교하는 것이다. 다만 [math]\displaystyle{ a\neq b }[/math]라고만 표현하면 어느 쪽이 더 큰지 작은지 비교를 할 수 없기 때문에 [math]\displaystyle{ \lt ,\gt ,\leq,\geq }[/math]와 같은 기호를 동원한다. 각 기호의 뜻은 차례대로 "작다 (미만)", "크다 (초과)", "작거나 같다 (이하)", "크거나 같다 (이상)"이다. 간혹 [math]\displaystyle{ \ll }[/math]나 [math]\displaystyle{ \gg }[/math]를 쓰기도 하는데, 이는 각각 "아주 작다", "아주 크다"를 의미한다. 넘사벽 다만 이 크기 비교는 자연수나 실수같이 크기가 정렬된 집합 (ordered set)에서만 성립한다. 고등학교 때 복소수의 부등식은 없다고 배울 텐데, 그 이유가 바로 복소수 집합은 크기가 정렬되어 있지 않기 때문.

방정식과 마찬가지로, 부등식은 그 자체로는 명제가 될 수 없다. 조건에 따라 참, 거짓이 달라지기 때문. 하지만 방정식에 항등식이 있듯이, 부등식에도 항상 성립하는 부등식인 절대부등식이 존재한다.

한국의 교육과정에선 방정식을 배운 뒤 세트로 같이 배우게 된다. 방정식을 푸는 데 익숙한 학생들은 "뭐야? 똑같네?"라고 생각하게 되지만 뒤로 갈수록 방정식에서 쓰이는 기술과는 다른 기술이 쓰여 차이점이 벌어지게 된다. 사실 수학 경시대회를 봐도 방정식을 푸는 유형은 쉬운 문제에 속하고, 부등식을 증명하는 문제는 어려운 문제에 속한다. 하지만 사기 기술 미적분이 등장하면 어떨까? 또한 한국 교육과정에선 부등식을 직관적으로만 설명하는데, 부등식 [math]\displaystyle{ a\lt b }[/math]의 정의는 [math]\displaystyle{ b-a\gt 0 }[/math]이다. 다른 것이 하나도 없어보이지만 의외로 중요하다.

성질

앞으로 나오는 모든 문자는 특별한 말이 없는 한 모두 임의의 실수이다. 또한 특별한 말이 없는 한 다른 부등호 기호에도 모두 성립하는 성질이다.

1. 추이율: [math]\displaystyle{ a\leq b, b\leq c }[/math]이면 [math]\displaystyle{ a\leq c }[/math]가 성립한다. 단, 여기서 어느 하나라도 강부등호가 들어가면 결과에도 강부등호가 쓰인다. 추이율은 모든 부등호 기호에 대해 성립하나, 반사율과 대칭율은 부등호 기호에 따라서 성립하기도 하고 성립하지 않기도 한다. 반사율은 [math]\displaystyle{ \leq,\geq }[/math]의 경우만, 대칭율은 등호가 성립할 때만 성립한다. 따라서 부등호는 동치관계가 아니다.
2. 덧셈, 뺄셈: [math]\displaystyle{ a\leq b }[/math]일 때, [math]\displaystyle{ a+c\leq b+c, a-c\leq b-c }[/math]이다.
3. 곱셈, 나눗셈: [math]\displaystyle{ a\leq b }[/math]이고 [math]\displaystyle{ c\gt 0 }[/math]이면 [math]\displaystyle{ ac\leq bc,\,\frac{a}{c}\leq\frac{b}{c} }[/math]가, 만약 [math]\displaystyle{ c\lt 0 }[/math]이면 [math]\displaystyle{ ac\geq bc,\,\frac{a}{c}\geq\frac{b}{c} }[/math]가 성립한다. 특히, [math]\displaystyle{ a\leq b }[/math]이면 [math]\displaystyle{ -a\geq -b }[/math]가 성립한다. 알아놔야 할 점은 양변에 음수를 곱하면 부등호의 방향이 바뀐다는 것이다.
4. 역수: [math]\displaystyle{ 0\lt a\leq b }[/math]이면, [math]\displaystyle{ 0\lt \frac{1}{b}\leq\frac{1}{a} }[/math]가, [math]\displaystyle{ a\leq b\lt 0 }[/math]이면 [math]\displaystyle{ \frac{1}{b}\leq\frac{1}{a}\lt 0 }[/math]이, 그리고 [math]\displaystyle{ a\lt 0\lt b }[/math]이면 [math]\displaystyle{ \frac{1}{a}\lt 0\lt \frac{1}{b} }[/math]가 성립한다.
5. 보존성: 증가함수를 합성해도 부등호의 방향은 유지된다. 증가함수를 예로 들어보자. 함수 [math]\displaystyle{ f }[/math]가 단조 증가 함수라 가정하고, [math]\displaystyle{ a\leq b }[/math]라 하자. 그럼 [math]\displaystyle{ f\left(a\right)\leq f\left(b\right) }[/math]가 그대로 성립한다. [math]\displaystyle{ a\lt b }[/math]여도 그대로 성립한다. 만약 함수 [math]\displaystyle{ f }[/math]가 강증가 함수이고, [math]\displaystyle{ a\leq b }[/math]이면 [math]\displaystyle{ f\left(a\right)\leq f\left(b\right) }[/math], [math]\displaystyle{ a\lt b }[/math]이면 [math]\displaystyle{ f\left(a\right)\lt f\left(b\right) }[/math]가 성립한다. [math]\displaystyle{ f }[/math]가 감소함수이면 부등호 방향이 뒤집힌다. 참고로 이를 이용해서 일부 부등식을 쉽게 증명할 수 있다. 부등식에 지수가 많으면 로그을 이용, 그후 미분을 사용하는 식으로.
6. [math]\displaystyle{ a\lt b }[/math]라 하자. 그럼 이는 적당한 실수 [math]\displaystyle{ r\gt 0 }[/math]이 존재하여 [math]\displaystyle{ a+r=b }[/math]를 만족함과 동치이다. 만약 [math]\displaystyle{ a\leq b }[/math]이면 적당한 실수 [math]\displaystyle{ r\geq0 }[/math]이 존재하여 [math]\displaystyle{ a+r=b }[/math]를 만족함과 동치. 이를 사용하여 부등식을 방정식 문제로 바꿀 수 있다.

1번부터 5번까지의 기본 성질은 모두 실수의 기본 성질과 6번 성질, 그리고 정의를 사용하여 증명이 가능하다. 증명이 어렵지 않으므로 관심 있는 위키러는 직접 해보자.

부등식의 해법

풀이는 대체로 방정식과 비슷한 느낌으로 하면 된다. 부등식의 성질과 마찬가지로 아래 부등식의 모든 예는 특별한 말이 없는한 모든 부등호에 대해 성립한다.

일변수 부등식

중학교, 고등학교에서 주로 풀게 되는 부등식. 식으로는 [math]\displaystyle{ a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0\gt 0 }[/math] 혹은 [math]\displaystyle{ a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0\geq0 }[/math]의 형태의 부등식을 말한다.

일차부등식

[math]\displaystyle{ ax+b\lt 0 }[/math] 혹은 [math]\displaystyle{ ax+b\leq0 }[/math] 형태의 부등식. 일차방정식과 마찬가지로 세 가지 경우로 나뉜다.

1. [math]\displaystyle{ a\neq0 }[/math]: [math]\displaystyle{ b }[/math]를 넘겨준뒤 [math]\displaystyle{ a }[/math]를 양변에 나눠주면 된다. 이 때 [math]\displaystyle{ a }[/math]가 양수냐 음수냐에 따라 부등호의 방향이 바뀌므로 주의.
2. [math]\displaystyle{ a=0, b\lt 0 }[/math]: [math]\displaystyle{ x }[/math]값에 관계없이 항상 성립하므로 절대부등식이 된다.
3. [math]\displaystyle{ a=0, b\geq0 }[/math]: [math]\displaystyle{ x }[/math]값에 관계없이 항상 성립하지 않으므로 모순이 된다.

이차부등식

[math]\displaystyle{ ax^2+bx+c\lt 0 }[/math] 혹은 [math]\displaystyle{ ax^2+bx+c\leq0 }[/math] 형태의 부등식. 여기서 부터 방정식과 풀이법이 조금씩 달라지기 시작한다. 풀이는 아래와 같다.

1. 먼저 [math]\displaystyle{ x^2 }[/math]의 계수를 양수로 바꿔준다.
2. [math]\displaystyle{ ax^2+bx+c=0 }[/math]의 근을 구한다. 근을 [math]\displaystyle{ \alpha, \beta }[/math]라 하자. (단 [math]\displaystyle{ \alpha\leq\beta }[/math])
3. 만약 부등호가 [math]\displaystyle{ \gt 0 }[/math]이면, [math]\displaystyle{ x\lt \alpha, x\gt \beta }[/math]가 답. 부등호가 [math]\displaystyle{ \geq }[/math]이면 답에도 등호가 들어간다. 단, [math]\displaystyle{ \alpha=\beta }[/math]일 경우 전자는 [math]\displaystyle{ x=\alpha }[/math]를 제외한 모든 값, 후자는 모든 [math]\displaystyle{ x }[/math]값이 답이다.
4. 부등호가 [math]\displaystyle{ \lt 0 }[/math]이면 [math]\displaystyle{ \alpha\lt x\lt \beta }[/math]가 답. 부등호가 [math]\displaystyle{ \leq }[/math]이면 답에도 등호가 들어간다. 단, [math]\displaystyle{ \alpha=\beta }[/math]일 경우 전자는 답이 없음, 후자는 [math]\displaystyle{ x=\alpha }[/math]만 답.

사실 이렇게 복잡한 과정을 거치지 않고 그래프를 활용하여 해결할 수 있다. 이는 바로 아래 문단 참조.

삼차부등식

방정식은 근의 공식이 4차까지 존재하기 때문에 위 이차 부등식의 풀이와 비슷하게 해법 알고리즘을 짤 수 있지만 그러기엔 너무 비효율적이다. 여기서 부터는 함수의 그래프를 적극 활용하게 된다. 풀이 방법은 아래와 같다.

1. 부등식을 방정식으로 바꿔준 뒤 근을 전부 구한다.
2. 수직선에 근을 찍고 그래프의 개형을 그려준다.
3. 부등호가 [math]\displaystyle{ \lt }[/math]나 [math]\displaystyle{ \leq }[/math]였다면 수직선 아랫부분에 해당하는 [math]\displaystyle{ x }[/math]값이 답.
4. 부등호가 [math]\displaystyle{ \gt }[/math]나 [math]\displaystyle{ \geq }[/math]였다면 수직선 윗부분에 해당하는 [math]\displaystyle{ x }[/math]값이 답. {

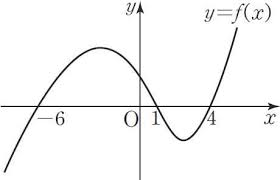
[math]\displaystyle{ \left(x+6\right)\left(x-1\right)\left(x-4\right)\lt 0 }[/math]을 예로 들면, 위 그래프에서 [math]\displaystyle{ x }[/math]축 아래에 해당하는 부분, 즉 [math]\displaystyle{ x\lt -6, 1\lt x\lt 4 }[/math]가 답이 된다.

사차부등식

삼차부등식과 마찬가지로 부등식을 방정식으로 바꾼 뒤 근을 전부 구하고 그래프를 이용하여 해를 구하면 된다. 사실 이 그래프를 이용하는 방법은 거의 모든 부등식에 사용이 가능하다.

여러 가지 부등식

1. 연립 부등식: 부등식이 여러 개 연결되어 있는 형태. 간단하게는 [math]\displaystyle{ a\lt b\lt c }[/math]도 [math]\displaystyle{ a\lt b }[/math]와 [math]\displaystyle{ b\lt c }[/math]의 연립 부등식이라 볼 수 있다. 풀이는 각 부등식을 따로 풀어준 뒤, 교집합에 해당하는 부분만 골라내면 된다.
2. 절댓값이 들어간 부등식: [math]\displaystyle{ \left|x\right|\lt a,\,\left(a\gt 0\right) }[/math]는 [math]\displaystyle{ -a\lt x\lt a }[/math], [math]\displaystyle{ \left|x\right|\gt a }[/math]는 [math]\displaystyle{ x\lt -a, x\gt a }[/math]와 동치임을 이용하여 절댓값을 벗겨준 뒤 부등식을 풀어주면 된다. 다만 이는 절댓값을 간단히 풀어줄 수 있을 때의 얘기고, 그렇지 않을 경우에는 그래프를 그려서 해결하자.
3. 분수 부등식: [math]\displaystyle{ \frac{1}{x+1}\leq\frac{1}{x^2+1} }[/math]과 같이 변수가 분모에도 있는 부등식을 말한다. 이를 풀 때는 부등식의 양변에 양수를 곱해도 부등호의 방향이 바뀌지 않는다는 성질을 이용한다. 다만 [math]\displaystyle{ x+1 }[/math]같은 경우는 양수인지 음수인지 확실히 알 수 없으므로 제곱을 해서 곱한다. 즉, 위 부등식의 경우에는 [math]\displaystyle{ \left(x+1\right)^2\left(x^2+1\right) }[/math]을 곱한 뒤 풀어준다. 주의할 점은, 분모를 0으로 만드는 [math]\displaystyle{ x }[/math]값을 체크해서 꼭 제외해 주어야 한다.
4. 무리 부등식: [math]\displaystyle{ \sqrt{x+1}\leq\sqrt{x^2+1} }[/math]과 같이 근호 안에 변수가 들어가 있는 부등식. 양변을 제곱하여 근호를 벗겨준 뒤 풀어주면 된다. 단, 근호 안을 음수로 만드는 [math]\displaystyle{ x }[/math]값은 반드시 제외해 주어야 한다.
5. 함수 부등식: 부등식에 지수, 로그, 삼각함수와 같은 것이 섞여있는 경우를 말한다. 보통 [math]\displaystyle{ f\left(x\right)\lt g\left(x\right) }[/math]의 형태로 나타난다. 푸는 방법은 바로 함수의 그래프를 이용하는 방법. 좌표계에 [math]\displaystyle{ f\left(x\right) }[/math]와 [math]\displaystyle{ g\left(x\right) }[/math]의 그래프를 각각 그려준 뒤, [math]\displaystyle{ f }[/math]가 [math]\displaystyle{ g }[/math]보다 아래 쪽에 있는 부분의 [math]\displaystyle{ x }[/math]값만 취해주면 된다. 혹은 [math]\displaystyle{ f\left(x\right)-g\left(x\right) }[/math]의 그래프를 그린 뒤 [math]\displaystyle{ x }[/math]축 아래에 있는 부분을 취해도 된다. 양변 다 지수함수거나 로그함수일 경우는 부등식의 보존성을 활용할 수도 있다. 예를 들어 [math]\displaystyle{ 2^x\lt 2^{3x+1} }[/math]을 푼다고 하자. 그럼 [math]\displaystyle{ 2^x }[/math]는 강증가 함수이므로 간단하게 [math]\displaystyle{ x\lt 3x+1 }[/math]만 풀어줘도 된다.

다변수 부등식

변수가 [math]\displaystyle{ x }[/math]하나만 있는 게 아닌 [math]\displaystyle{ y,z }[/math]등 2개 이상이 있는 부등식. 여기서 부터는 함수의 그래프가 필수다. 또한 답도 1차원적으로 간단히 나오는 게 아니라 특정 영역의 형태로 나타나게 된다. 예로 [math]\displaystyle{ x^2+y^2\lt 1 }[/math]의 경우는 원 안의 영역에 해당하는 모든 [math]\displaystyle{ x,y }[/math]값이 답이 된다. 답을 제출할 때에는 그래프를 그린 뒤 영역을 색칠(...)하면 된다. 대한민국의 수학 교육과정에서는 보통 이차곡선을 배울 때 자주 하게 된다.

부등식의 영역

위에 잔뜩 부등식의 풀이법을 적어 놨지만, 사실 그 모든 것은 이 부등식의 영역 하나로 해결할 수 있다. 최종보스 한국의 교육과정에는 1차원 부등식의 영역과 2차원 부등식의 영역, 이 두 개만 색칠할 수 있으면 된다.

1차원 부등식의 영역은 뭔가 거창한 이름이지만 사실 초등학교 때 부터 해온 수직선 위 색칠놀이이다. 등호가 들어가 있으면 색칠 된 원, 등호가 없으면 색칠 안 된 원으로 나타내며, 부등호에 따라 오른쪽(큰 쪽), 왼쪽(작은 쪽)을 칠하면 된다.

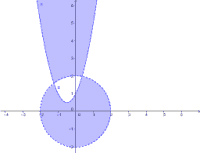
2차원 부등식의 영역은 고등학교 때 부터 위키러들을 잔뜩 괴롭힐 위 직교좌표계 위 색칠놀이이다. 부등호에 등호가 들어가 있으면 경계선을 실선으로, 없으면 점선으로 표시한다. 점의 경우는 수직선 위 부등식의 영역과 마찬가지로 포함되면 색칠, 아니면 비워둔다. 그런데 이 2차원 부등식의 영역이 보통 귀찮은게 아닌데, 하나 그리기도 짜증나는 복잡한 함수들의 그래프를 그린 뒤, 각 부등식에 해당하는 부분을 색칠하고, 최종적으로는 모두 겹치는 부분만 남겨야 한다. 게다가 그래프의 교점도 찾아야 하므로 방정식도 풀어야 한다! 점선과 실선을 헷갈린다든가, 교점이 포함되는지 제외되는지 헷갈린다든가, 아니면 통째로 색칠해야 하는 부분을 틀린다던가……. 안습

절대부등식

이와 관련한 주제는 절대부등식에서 다룹니다.

항등식과 대응되는 개념. 부등식 내 변수에 어떤 값을 대입하더라도 항상 성립하는 부등식을 말한다.

부등식 목록

• 산술·기하 평균 부등식
• 평균부등식
• 재배열 부등식
• 코시-슈바르츠 부등식
• 슈르 부등식
• 젠센 부등식
• 베르누이 부등식
• 삼각부등식
• 홀더 부등식
• 민코프스키 부등식
• 뮤어헤드 부등식
• 오일러 부등식

같이 보기

• 등호
• 방정식
• 항등식
• 부등호
• 절대부등식