기하학에서 육각형(六角形)은 변이 여섯 개인 도형이다. 육각형의 내각의 합은 720°이다.
정육각형[편집 | 원본 편집]
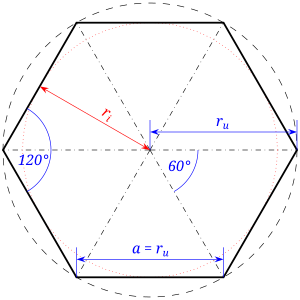
정육각형(正六角形)의 한 각의 크기는 120°이므로 한 꼭짓점에 3개의 정육각형이 모인 {6,6,6} 형태로 테셀레이션이 가능하다. 또한 정육각형은 {3,6,3,6}, {3,4,4,6}, {4,6,12}, {3,3,3,3,6} 형태의 준정다각형 테셀레이션의 하나의 구성 요소가 된다. 그리고 밑면이 정육각형인 육각기둥은 평행이동으로 공간을 채울 수 있는 공간도형이다.
한 변의 길이가 [math]\displaystyle{ a }[/math]인 정육각형의 넓이는 다음과 같다.
- [math]\displaystyle{ A = \frac{3 \sqrt{3}}{2}a^2 \simeq 2.59808 a^2 }[/math]
작도[편집 | 원본 편집]

정육각형을 작도하는 과정
왼쪽 그림과 같이 정육각형은 다음과 같이 원 위에 작도할 수 있다.
1. 우선 원 O를 그린 뒤, 원의 지름을 그린다. 원의 지름과 원은 교점 X,Y에서 만난다.
2. 그려진 원 O의 반지름을 반지름으로 하고, 원의 한 점 X를 중심으로 하는 새로운 원을 그린다. 새로 그린 원은 원래의 원과 교점이 2개(A,B)가 생긴다. (XoA, XoB는 각도가 60도이다.)
3. 그 다음에 각각 점 A, B를 지나는 원 O의 지름을 그린다. 그러면 점 A, B의 반대편의 교점이 만들어진다. 그러면 처음 원의 지름의 교점과 점 A, B를 지나는 세 지름에 의해 생긴 여섯 점은 정육각형의 꼭짓점이 된다.
작도 원리는 의외로 간단한데, 정육각형을 분할하여 만드는 정삼각형의 외심이 갖는 성질을 거꾸로 이용한 것이다.
자연에서 볼 수 있는 육각형[편집 | 원본 편집]
다각형 목록 |
|
|---|---|
| 삼각형 | |
| 사각형 | |
| 그밖의 도형 | |