Tessellation
개요[편집 | 원본 편집]
테셀레이션이란 하나, 혹은 여러 개의 도형으로 평면을 겹치지 않고, 빈틈 없이 채우는 것을 말한다. 수학에서는 평면 뿐만 아니라 3차원 공간, 혹은 임의의 n차원의 하이퍼스페이스를 채우는 것도 포함한다. 테셀레이션은 실생활에서 의외로 자주 볼 수 있는데, 보도블럭 모양이나, 칠교놀이, 그리고 벌집의 육각형 모양도 테셀레이션의 일종이다.
수학에서[편집 | 원본 편집]
테셀레이션에 쓰이는 도형의 종류와 개수에 따라 여러 세부 분류가 존재한다.
- 정규 테셀레이션: 한 종류의 정다각형만으로 평면을 채우는 것. 삼각형, 사각형, 육각형의 세 가지 경우만 존재한다. 이유는 간단한데, 내각을 더해 360도가 가능한 다각형이 이 3개 밖에 없기 때문.
- 준정규 테셀레이션: 두 종류 이상의 정다각형으로 평면을 채우되, 꼭짓점에 모이는 정다각형의 개수와 규칙이 같은 경우를 말한다. 8가지만 존재한다.
- 비정규 테셀레이션: 정다각형을 사용해 그냥 막 평면을 채운 경우.
- 허니콤 (Honeycomb): 평면이 아닌 3차원 이상의 공간을 테셀레이션 하는 걸 말한다. 간단하게는 정육면체로 공간을 채우는 것도 허니콤의 일종.
자가복제도형[편집 | 원본 편집]
영어로는 Repetition-tile, 혹은 줄여서 Rep-tile이라 부른다.[1] 테셀레이션의 특별한 경우로서, 평면 전체가 아닌 특정한 모양의 평면을 채우는데, 그 평면의 모양과 같은 도형으로만 채우는 것을 말한다. 또한 채우는 도형은 (일반적으로) 모두 합동이여야 한다. 자가복제도형의 몇 가지 성질은 다음과 같다.
- 폴리노미노[2]가 정사각형, 혹은 직사각형을 덮을 수 있다면, 원 도형은 자가복제도형이다. 이유는 간단한데, 직사각형은 정사각형을 덮을 수 있고, 폴리노미노는 정사각형으로만 이루어진 도형이기 때문.
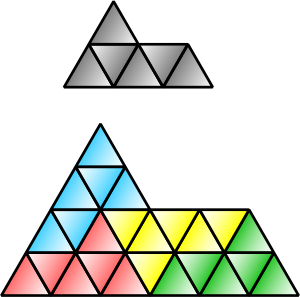
- 폴리아몬드[3]가 정삼각형을 덮을 수 있다면, 원 도형은 자가복제도형이다. 이유는 폴리노미노와 동일.
- 폴리아볼로[4]가 직각이등변삼각형을 덮을 수 있다면, 원 도형은 자가복제도형이다. 이유는 위와 동일.
- 자가복제도형은 모두 테셀레이션이 가능한 도형이다. 자가복제도형을 테셀레이션의 하위 분류로 만들어 주는 이유. 특정한 모양의 평면이 자가복제도형으로 덮어졌으면, 그 평면을 자가복제 해서 더 큰 평면을 덮는 식으로 평면 전체를 덮을 수 있다.