Isosceles Triangle
정의[편집 | 원본 편집]
삼각형 중, 두 변의 길이가 같은 삼각형을 이르는 단어. 중학교 2학년 때 처음 증명을 배우면서 자세히 다루게 되는 도형이다.
성질[편집 | 원본 편집]
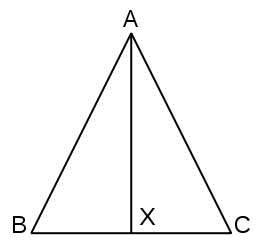
- 꼭짓점에서 밑변에 내린 수선은 밑변을 이등분한다. 역으로 한 꼭짓점에서 대변에 내린 수선이 대변을 이등분하면 그 삼각형은 이등변삼각형이다.
- 꼭짓점에서 밑변에 내린 중선은 밑변과 직교한다.
- 꼭짓점에서 밑변에 내린 수선, 혹은 중선은 각을 이등분한다.
- 두 밑각의 크기가 같다. 역으로 두 각의 크기가 같은 삼각형은 이등변삼각형이다
증명[편집 | 원본 편집]
1. [math]\displaystyle{ \overline{AB}=\overline{AC},\,\angle{AXB}=\angle{AXC}=\angle{R},\,\overline{AX} }[/math]공통 이므로 [math]\displaystyle{ \triangle{AXB}\cong\triangle{AXC} }[/math] (RHS 합동). 따라서 [math]\displaystyle{ \overline{BX}=\overline{CX} }[/math]. 역의 증명은 다음과 같다. [math]\displaystyle{ \overline{BX}=\overline{CX},\,\angle{AXB}=\angle{AXC}=\angle{R},\,\overline{AX} }[/math]공통 이므로 [math]\displaystyle{ \triangle{AXB}\cong\triangle{AXC} }[/math] (SAS 합동). 따라서 [math]\displaystyle{ \overline{AB}=\overline{AC} }[/math].
2. [math]\displaystyle{ \overline{AB}=\overline{AC},\,\overline{BX}=\overline{CX},\,\overline{AX} }[/math]공통 이므로 [math]\displaystyle{ \triangle{AXB}\cong\triangle{AXC} }[/math] (SSS 합동). 따라서 [math]\displaystyle{ \angle{AXB}=\angle{AXC} }[/math], 그리고 [math]\displaystyle{ \angle{AXB}+\angle{AXC}=180^\circ }[/math]이므로 [math]\displaystyle{ \angle{AXB}=\angle{R} }[/math].
3, 4. 1번과 2번 증명을 참고하자. 증명 중에 같이 증명된다.
기타[편집 | 원본 편집]
- 만약 두 변 뿐만이 아니라 나머지 한 변의 길이도 같으면 정삼각형이 된다.
- 꼭지각이 직각이면 직각이등변삼각형이 된다. 직각이등변삼각형은 직각삼각형과 이등변삼각형의 성질을 모두 만족한다.
- 밑변에 대칭으로 같은 삼각형을 이어붙이면 마름모가 된다. 옆변에 이어붙이면 평행사변형이 된다.
- 세 변의 길이가 주어졌을 때, 헤론의 공식을 쓰지 않고도 넓이를 쉽게 구할 수 있다. 피타고라스 정리를 사용하자.
관련 항목[편집 | 원본 편집]
다각형 목록 |
|
|---|---|
| 삼각형 | |
| 사각형 | |
| 그밖의 도형 | |