기하학에서 십칠각형(十七角形, Heptadecagon) 및 17면체는 변과 각이 모두 17개인 평면도형을 말한다.
정십칠각형[편집 | 원본 편집]
정십칠각형의 한 내각은 약 158.82도이며, 모든 내각의 합은 2700도이다.
정십칠각형은 작도가 가능한 평면도형인데, 이는 2π⁄17의 삼각함수가 사칙연산과 제곱근만으로 표현이 가능하다는 것을 의미한다.
정십칠각형의 한 변의 길이를 t라고 하면, 정십칠각형의 넓이는 다음 식과 같다.
- [math]\displaystyle{ \frac{17}{4}t^2 \cot \frac{\pi}{17} }[/math]
작도[편집 | 원본 편집]
우선 정십칠각형의 작도법을 이해하기 위해서는 아래 드 무아부르의 법칙을 이해해야 한다.
[math]\displaystyle{ (\cos \theta + i \sin \theta)^n = \cos n\theta + i \sin n \theta }[/math] 여기서 n은 자연수이다. 그러면 이 공식을 이용해서 1의 17제곱근들을 구하면 [math]\displaystyle{ \zeta_{17} = \cos \frac{2 k \pi}{17} + i \sin \frac{2 k \pi}{17} }[/math]가 나온다. 여기서 k는 임의의 자연수.
또한 3이 법(modulo) 17에 대해 원시근(primitive root)임을 알 수 있고, 또한 우리는 17에 대한 이차 잉여류 제곱인 [math]\displaystyle{ {\zeta_{17}} , {\zeta_{17}}^2 , {\zeta_{17}}^4 , {\zeta_{17}}^8 , {\zeta_{17}}^{9}, {\zeta_{17}}^{13}, {\zeta_{17}}^{15}, {\zeta_{17}}^{16} }[/math]의 합을 A0, 이차 비잉여류(quadratic nonresidue) 제곱인 [math]\displaystyle{ {\zeta_{17}}^3 , {\zeta_{17}}^5 , {\zeta_{17}}^6 , {\zeta_{17}}^7 , {\zeta_{17}}^{10}, {\zeta_{17}}^{11}, {\zeta_{17}}^{12}, {\zeta_{17}}^{14} }[/math]의 합을 A1으로 놓는다. 계산하면 A0+A1=-1, A0·A1=-4임을 알 수 있으며, A0>A1이므로
[math]\displaystyle{ \text{A0} = \frac{-1+\sqrt{17}}{2} , \text{A1}= \frac{-1-\sqrt{17}}{2} }[/math].
또한 3을 원시근으로 놓을 때 법 17에 대한 지수는 법 φ(17)에 대해 다음과 같이 구해진다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 0 | 14 | 1 | 12 | 5 | 15 | 11 | 10 | 2 | 3 | 7 | 13 | 4 | 9 | 6 | 8 |
4로 나누었을 때 나머지가 같은 지수 [math]\displaystyle{ {\zeta_{17}}^{3^{4k+r}} }[/math]끼리 모아서 더한 값들을 각각 B0, B1, B2, B3이라고 놓자. 당연히 B0+B2=A0, B1+B3=A1이 된다.
[math]\displaystyle{ {\zeta_{17}} + {\zeta_{17}}^{4} + {\zeta_{17}}^{13} + {\zeta_{17}}^{16} = \text{B0} }[/math]
[math]\displaystyle{ {\zeta_{17}}^{3} + {\zeta_{17}}^{5} + {\zeta_{17}}^{12} + {\zeta_{17}}^{14} = \text{B1} }[/math]
[math]\displaystyle{ {\zeta_{17}}^{2} + {\zeta_{17}}^{8} + {\zeta_{17}}^{9} + {\zeta_{17}}^{15} = \text{B2} }[/math]
[math]\displaystyle{ {\zeta_{17}}^{6} + {\zeta_{17}}^{7} + {\zeta_{17}}^{10} + {\zeta_{17}}^{11} = \text{B3} }[/math]
그런데 공교롭게도 B0·B2=-1, B1·B3=-1이 된다. 따라서 근의 공식을 활용하면.
[math]\displaystyle{ \text{B0} = \frac{-1+\sqrt{17} + \sqrt{34 - 2 \sqrt{17}}}{4}, \\ \text{B1} = \frac{-1-\sqrt{17} + \sqrt{34 + 2 \sqrt{17}}}{4}, \\ \text{B2} = \frac{-1+\sqrt{17} - \sqrt{34 - 2 \sqrt{17}}}{4}, \\ \text{B3} = \frac{-1-\sqrt{17} - \sqrt{34 + 2 \sqrt{17}}}{4} }[/math].
마지막으로 C0 = ζ17+ζ1716를 구해보자. C4= ζ174+ζ1713이라고 놓으면 C0+C4=B0, C0·C4=B1이 되고, 따라서 C0>C4를 이용하면
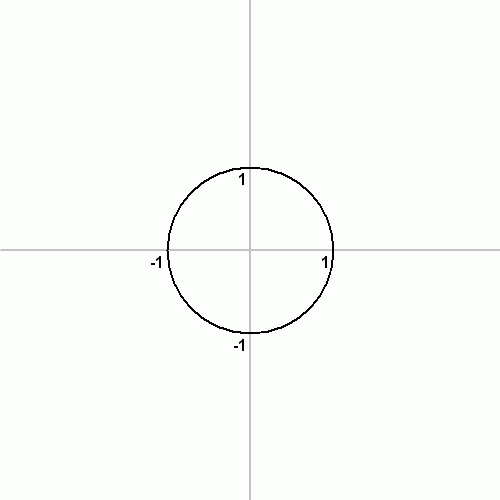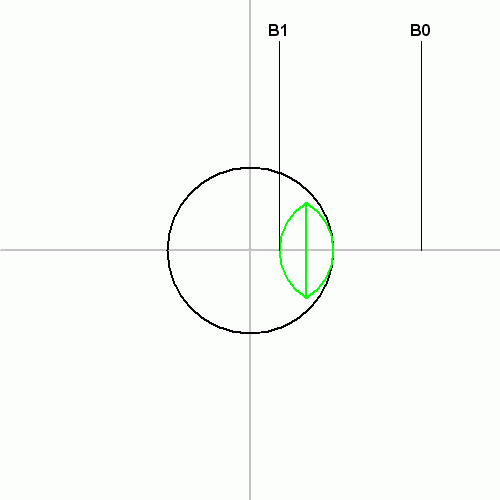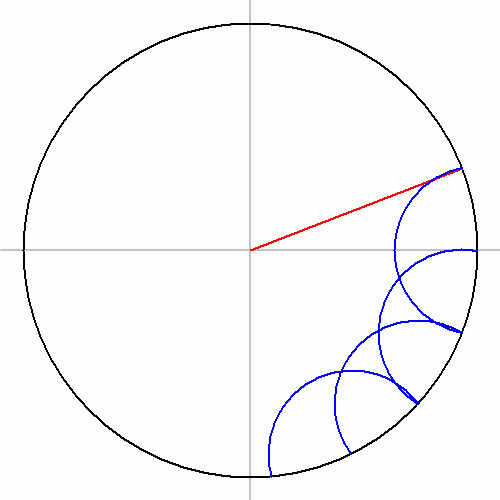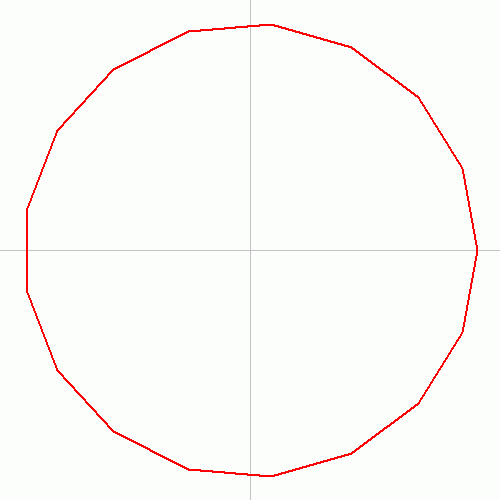
[math]\displaystyle{ \text{C0} = {\zeta_{17}} + {\zeta_{17}}^{16} = \frac{\text{B0} + \sqrt{\text{B0}^2 -4 \cdot \text{B1}}}{2} }[/math]가 나온다. 여기서 C0=2cos(2π/17)인 실수가 되므로 반지름이 1이고 중심이 원점 O인 원 P에 대해 반지름의 연장선을 그린 뒤 거리가 C0가 되는 점까지 표시한다. O~C0에 대한 수직이등분선을 작도하면 수직이등분선과 원이 만나는 두 점(D0, D1)은 O~C0와 원이 만나는 점(C')과 정확히 2π/17만큼의 각을 이룬다. 즉 반지름의 길이가 C'D0인 원을 중심 D0에서 그리면 원래의 원 P와 한 점 C' 이외에 다른 점 D2에서 만난다. 이제 원 D2를 중심으로 하고 반지름의 길이가 C'D0인 원을 그리면서 새로운 교점을 D3로 놓는다. 이런 식으로 반복해서 교점을 작도하면 정십칠각형이 작도된다는 것을 알 수 있다.
정십칠각형이 눈금 없는 자와 컴퍼스로 작도되므로 정34(17×2)각형, 정51(17×3)각형, 정85(17×5)각형도 작도가 가능하다는 것을 알 수 있다. 또한 카를 프리드리히 가우스(Carl Friedrich Gauss)는 정십칠각형의 작도법을 찾았을 뿐 아니라 페르마 소수 Fn에 대해서 정(Fn)각형도 눈금 없는 자와 컴퍼스로 작도가 가능하다는 것을 보였다. 즉 정257각형과 정65537각형도 작도가 가능하다는 이야기이다. 물론 증명방법은 엄청나게 지루하기에 생략한다.
다각형 목록 |
|
|---|---|
| 삼각형 | |
| 사각형 | |
| 그밖의 도형 | |