사다리꼴

Trapezoid

정의

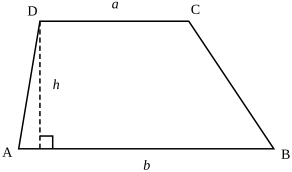
사각형의 특수한 경우 중 하나로, 한 쌍의 대변이 평행한 사각형을 말한다. 평행한 두 대변을 윗변과 밑변, 평행하지 않은 두 변을 빗변이라 부른다. 두 빗변의 길이가 같다면 그 사다리꼴은 등변사다리꼴이 된다. 한국의 수학 교육과정에서는 사다리꼴에 대한 많은 성질을 배우진 않지만, 파고들면 상당히 복잡하고 중요한 성질이 많은 사각형.

성질

1. 빗변을 기준으로 이웃한 두 각은 서로 보각관계이다. 즉, 두 각의 합이 180도.
2. 사다리꼴의 넓이는 [math]\displaystyle{ S=\frac{a+b}{2}h }[/math]
3. 두 대각선은 서로를 각각 윗변과 밑변의 비로 나눈다.
4. 두 대각선을 그어서 생기는 네 개의 삼각형 중 빗변을 포함한 두 삼각형은 넓이가 같다.
5. 밑변과 윗변의 중점과 두 대각선의 교점은 공선점이다.

등변사다리꼴의 성질

1. 두 밑각의 크기가 같다. 역으로 사다리꼴의 두 밑각의 크기가 같으면 등변사다리꼴이다.
2. 두 대각선의 길이는 같다.
3. 등변사다리꼴은 반드시 원에 내접한다.

증명

1. 엇각을 이용하자.
2. 사다리꼴을 뒤집어서 이어 붙이면 평행사변형이 된다. 그 평행사변형의 넓이는 [math]\displaystyle{ \left(a+b\right)h }[/math]이고, 사다리꼴의 넓이는 그 평행사변형의 넓이의 절반이므로 [math]\displaystyle{ S=\frac{a+b}{2}h }[/math]

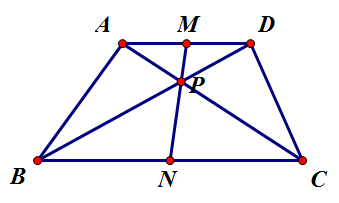
3. [math]\displaystyle{ \overline{AD}\parallel\overline{BC} }[/math]이므로, [math]\displaystyle{ \angle{CAD}=\angle{ACB}, \angle{BDA}=\angle{DBC} }[/math] (엇각). [math]\displaystyle{ \therefore\triangle{APD}\sim\triangle{CPB} }[/math], 두 닮은 삼각형의 길이의 비는 [math]\displaystyle{ \overline{AD}:\overline{BC} }[/math]이다. 따라서 두 대각선은 서로를 각각 윗변과 밑변의 비로 나눈다.

4. [math]\displaystyle{ \overline{AD}=a,\overline{BC}=b }[/math]라 하자. 3번 성질에 의해 적당한 실수 [math]\displaystyle{ p,q }[/math]에 대해 [math]\displaystyle{ \overline{AP}=ap, \overline{CP}=bp, \overline{DP}=aq, \overline{BP}=bq }[/math]가 성립한다. 또한 [math]\displaystyle{ \angle{APB}=\angle{CPD} }[/math] (맞꼭지각)이다. 이 각의 크기를 [math]\displaystyle{ \theta }[/math]라 하자. 그럼 [math]\displaystyle{ \triangle{APB} }[/math]의 넓이는 [math]\displaystyle{ \frac{1}{2}\times ap\times bq\times\sin\theta=\frac{1}{2}abpq\sin\theta }[/math], [math]\displaystyle{ \triangle{CPD} }[/math]의 넓이는 [math]\displaystyle{ \frac{1}{2}\times aq\times bp\times\sin\theta=\frac{1}{2}abpq\sin\theta }[/math]. 따라서 [math]\displaystyle{ S_{\triangle{APB}}=S_{\triangle{CPD}} }[/math].

5. 윗변과 밑변의 중점을 각각 [math]\displaystyle{ M,N }[/math]이라 하자. 그럼 3번 성질을 이용해 [math]\displaystyle{ \triangle{APM}\sim\triangle{CPN} }[/math](SAS 닮음)임을 보일 수 있다. 따라서 [math]\displaystyle{ \angle{APM}=\angle{CPN} }[/math]. 마찬가지로 3번 성질을 이용해 [math]\displaystyle{ \triangle{DPM}\sim\triangle{BPN} }[/math](SAS 닮음)임을 보일 수 있다. 따라서 [math]\displaystyle{ \angle{DPM}=\angle{BPN} }[/math]. 한편, 두 대각선에 대해 맞꼭지각이 성립하므로, [math]\displaystyle{ \angle{DPC}=\angle{APB} }[/math]. 따라서 [math]\displaystyle{ \angle{MPC}=\angle{NPA} }[/math]. 대각선 [math]\displaystyle{ \overline{AC} }[/math]와 선 [math]\displaystyle{ MPC }[/math]에 대해 두 맞꼭지각이 성립하므로 세 점 [math]\displaystyle{ M,P,N }[/math]은 공선점이다.

등변사다리꼴

1. 두 빗변의 크기가 같다고 가정하자. 윗변의 꼭짓점 [math]\displaystyle{ A,D }[/math]에서 밑변에 내린 수선의 발을 각각 [math]\displaystyle{ E,F }[/math]라 하자. 그럼 [math]\displaystyle{ \overline{AB}=\overline{CD},\overline{AE}=\overline{DF},\angle{AEB}=\angle{DFC}=\angle{R} }[/math]이므로 [math]\displaystyle{ \triangle{ABE}\cong\triangle{DCF} }[/math](RHS 합동)이다. 따라서 [math]\displaystyle{ \angle{B}=\angle{C} }[/math]. 이제 역으로 두 밑각의 크기가 같다고 가정하자. 그럼 [math]\displaystyle{ \overline{AE}=\overline{DF},\angle{AEB}=\angle{DFC}=\angle{R}, \angle{B}=\angle{C} }[/math]이므로 [math]\displaystyle{ \triangle{ABE}\cong\triangle{DCF} }[/math](RHA 합동)이다. 따라서 [math]\displaystyle{ \overline{AB}=\overline{CD} }[/math].
2. [math]\displaystyle{ \overline{AB}=\overline{CD},\angle{B}=\angle{C} }[/math]이고 [math]\displaystyle{ \overline{BC} }[/math] 공통이므로 [math]\displaystyle{ \triangle{ABC}\cong\triangle{DCB} }[/math](SAS 합동)이다. 따라서 [math]\displaystyle{ \overline{AC}=\overline{BD} }[/math]
3. 2번 성질의 증명에서 [math]\displaystyle{ \triangle{ABC}\cong\triangle{DCB} }[/math]이다. 따라서 [math]\displaystyle{ \angle{BAC}=\angle{CDB} }[/math]이고, 이는 원주각을 만족한다. 따라서 등변사다리꼴은 원에 내접한다.

관련 항목

• 사각형
• 평행사변형
• 마름모
• 직사각형
• 정사각형
• 중점연결정리