사각형

Quadrilateral

개요

삼각형이 도형을 처음 배우는 초등학교 때 부터 대학교 때까지 쭉 직접적으로 나와 괴롭힌다면, 사각형은 뒤에서 지원사격을 해주는 그런 존재. 여러 가지 성질을 자세하게 배우는 삼각형에 비해 사각형은 그렇게 많은 성질을 배우지 않는다. 하지만 KMO같은 수학 경시대회를 준비한다면 "사각형에 이런 성질이 있어?"싶은 사각형만의 많은 성질들을 배우게 될 것이다. 기호로는 [math]\displaystyle{ \square }[/math]가 있지만 [math]\displaystyle{ \triangle }[/math]에 비해 거의 쓰이지 않는다. 콩라인. 그러고 보니 4=2x2네?

용어

• 대변 (대각): 한 변(각)을 기준으로 마주보고 있는 변(각). 삼각형과의 차이점은, 각에 대한 대변(변에 대한 대각)은 존재하지 않는다는 것이다.
• 사다리꼴: 한 쌍의 대변이 평행한 사각형.
• 등변사다리꼴: 사다리꼴의 특수한 경우로, 평행하지 않은 두 변의 길이가 같은 사다리꼴을 말한다.
• 평행사변형: 두 쌍의 대변이 각각 평행한 사각형.
• 마름모: 네 변의 길이가 같은 사각형.
• 직사각형: 네 각의 크기가 모두 같은 사각형.
• 정사각형: 네 변의 길이와 네 각의 크기가 모두 각각 같은 사각형.
• 오목사각형: 한 각의 크기가 180도를 넘어가는 사각형. 오목사각형이 아니면 볼록사각형이라 부른다.

사각형의 성질

사다리꼴, 평행사변형, 마름모, 직사각형, 정사각형에 대한 성질은 각 항목을 참조하자.

내접 사각형

중학교 때 배우는 원과 사각형의 중요한 성질. 사각형이 원에 내접하기 위한 조건은 아래와 같다.

• 대각의 크기의 합이 180도이다.
• 한 외각의 크기가 내대각의 크기와 같다.
• 원주각을 만족한다.
• 방멱의 정리를 만족한다.
• 톨레미의 정리를 만족한다.
• 네 꼭짓점에 이르는 거리가 같은 점이 존재한다.
• 네 변의 수직이등분선이 한 점에서 만난다.

위 조건을 만족하면 사각형이 원에 내접하는 이유는 각 항목과 공원점 항목을 참조하자. 여기서는 증명을 생략한다.

외접 사각형

내접 사각형은 학교에서 자세히 배우지만, 외접 사각형에 대해서는 학교에서 가르쳐주지 않는다. 사실 외접원과 달리 내접원은 조건이 조금 까다롭기 때문. 볼록사각형이 원에 외접하기 위한 조건은 아래와 같다.

• 두 쌍의 대변의 합이 같다. (듀란드의 문제)
• 네 변에 이르는 거리가 같은 점이 존재한다.
• 네 각의 이등분선이 한 점에서 만난다.

두번째 조건은 내접원의 정의이고, 세번째 조건에서 두번째 조건을 유도하기는 매우 쉬우므로 첫번째 조건만 증명한다.

듀란드의 문제

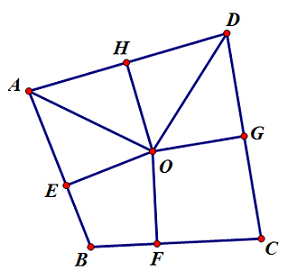
각 [math]\displaystyle{ A }[/math]와 [math]\displaystyle{ D }[/math]의 이등분선의 교점을 [math]\displaystyle{ O }[/math]라 하고, 점 [math]\displaystyle{ O }[/math]에서 각 변에 내린 수선의 발을 각각 [math]\displaystyle{ E,F,G,H }[/math]라 하자. 그럼 [math]\displaystyle{ \triangle{AOE}\cong\triangle{AOH} }[/math] (RHA 합동) 이므로 [math]\displaystyle{ \overline{OE}=\overline{OH} }[/math]이고, [math]\displaystyle{ \overline{AE}=\overline{AH} }[/math]이다. 비슷하게, [math]\displaystyle{ \triangle{DOH}\cong\triangle{DOG} }[/math]이므로 [math]\displaystyle{ \overline{OH}=\overline{OG} }[/math]이고 [math]\displaystyle{ \overline{DH}=\overline{DG} }[/math]이다. 이제 [math]\displaystyle{ \overline{OF}\gt \overline{OE} }[/math]라 가정하면 [math]\displaystyle{ \overline{BF}\lt \overline{BE} }[/math]이고 [math]\displaystyle{ \overline{CF}\lt \overline{CG} }[/math]이므로 [math]\displaystyle{ \overline{AD}+\overline{BC}-\overline{AB}-\overline{CD}=\overline{BE}+\overline{CG}-\overline{BF}-\overline{CF}\gt 0 }[/math]이므로 조건에 모순. 마찬가지로 [math]\displaystyle{ \overline{OF}\lt \overline{OE} }[/math]일 때도 모순이므로 [math]\displaystyle{ \overline{OF}=\overline{OE} }[/math]이고, 이는 사각형에 내접하는 원이 있음을 보인다.

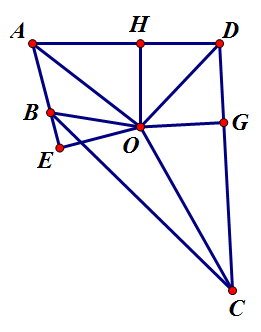
수학에 조금 관심이 있는 사람이라면 위 증명에서 예를 들어 어떻게 [math]\displaystyle{ E }[/math]가 항상 [math]\displaystyle{ \overline{AB} }[/math] 위에 있다고 보장할 수 있느냐 하는 의문이 들 수 있다. 그런데 볼록사각형의 두 쌍의 대변의 길이의 합이 같다면 [math]\displaystyle{ E }[/math]가 항상 [math]\displaystyle{ \overline{AB} }[/math] 위에 존재함을 보일 수 있다.

위 증명에서와 같이 [math]\displaystyle{ \angle{A} }[/math]와 [math]\displaystyle{ \angle{D} }[/math]의 이등분선의 교점을 [math]\displaystyle{ O }[/math]라 하고, 점 [math]\displaystyle{ O }[/math]에서 [math]\displaystyle{ \overline{AB},\,\overline{CD},\,\overline{DA} }[/math](혹은 그 연장선)에 내린 수선의 발을 각각 [math]\displaystyle{ E,G,H }[/math]라 하자. 그럼 [math]\displaystyle{ \triangle{AOE}\cong\triangle{AOH},\,\triangle{DOH}\cong\triangle{DOG} }[/math](RHA 합동)이다. 따라서 [math]\displaystyle{ \overline{OE}=\overline{OH}=\overline{OG} }[/math]이고, 이 길이를 [math]\displaystyle{ r }[/math]이라 하자.

이제 [math]\displaystyle{ \overline{AH}=\overline{AE}=a,\,\overline{DH}=\overline{DG}=b }[/math]라 하고, [math]\displaystyle{ \overline{BE}=x,\,\overline{CG}=y }[/math]는 ‘부호 있는 길이’로 생각하자. 즉, [math]\displaystyle{ E }[/math]가 [math]\displaystyle{ \overline{AB} }[/math] 위에 있다면 [math]\displaystyle{ \overline{AB}=a+x }[/math]로 그렇지 않으면 [math]\displaystyle{ \overline{AB}=a-x }[/math]로 나누어 적는 것은 불편하므로, 항상 [math]\displaystyle{ \overline{AB}=a+x }[/math]로 적되 [math]\displaystyle{ E }[/math]가 [math]\displaystyle{ \overline{AB} }[/math] 위에 있다면 [math]\displaystyle{ x\gt 0 }[/math]으로, 아니라면 [math]\displaystyle{ x\lt 0 }[/math]으로 이해하자는 것이다. 마찬가지로 [math]\displaystyle{ \overline{CD}=b+y }[/math]이고, [math]\displaystyle{ \overline{AB}+\overline{CD}=\overline{BC}+\overline{AD} }[/math]에서 [math]\displaystyle{ \overline{BC}=x+y }[/math]임을 알 수 있다. 마지막으로 피타고라스 정리에 의해 [math]\displaystyle{ \overline{AO}=\sqrt{a^2+r^2},\,\overline{BO}=\sqrt{x^2+r^2},\,\overline{CO}=\sqrt{y^2+r^2} }[/math]이다.

이제 [math]\displaystyle{ \angle{ABO}=\alpha,\,\angle{CBO}=\beta }[/math]라 하고, 이들의 값을 조사해 보자. 볼록사각형이므로 [math]\displaystyle{ \alpha+\beta=\angle{B}\lt 180^\circ }[/math]여야 한다.

먼저 [math]\displaystyle{ \angle{ABO}=\alpha }[/math]에 관해서는, [math]\displaystyle{ E }[/math]는 [math]\displaystyle{ O }[/math]에서 내린 수선의 발이라는 점을 이용해 [math]\displaystyle{ \cos\alpha = x/\sqrt{x^2+r^2} }[/math]를 얻는다.

다음 [math]\displaystyle{ \angle{CBO}=\beta }[/math]를 구하기 위해서는 코사인 법칙을 사용한다. [math]\displaystyle{ \triangle{CBO} }[/math]에서 [math]\displaystyle{ \left(x+y\right)^2+x^2+r^2-2\left(x+y\right)\sqrt{x^2+r^2}\cos\beta=y^2+r^2 }[/math]이고, 정리하면 [math]\displaystyle{ x\left(x+y\right)=\left(x+y\right)\sqrt{x^2+r^2}\cos\beta }[/math]가 된다. [math]\displaystyle{ x+y }[/math]는 길이이므로 0은 아닐 것이고, 따라서 [math]\displaystyle{ \cos\beta = x/\sqrt{x^2+r^2} }[/math]를 얻는다.

이제 [math]\displaystyle{ \cos\alpha = \cos\beta }[/math]이므로 [math]\displaystyle{ \alpha = \beta }[/math]이고, 주어진 사각형은 볼록사각형이므로 [math]\displaystyle{ \alpha = \beta \lt 90^\circ }[/math]여야 한다. 즉, [math]\displaystyle{ \cos\alpha = \cos\beta = x/\sqrt{x^2+r^2} \gt 0 }[/math]이어야 한다. 따라서 [math]\displaystyle{ x\gt 0 }[/math]이고 [math]\displaystyle{ E }[/math]가 [math]\displaystyle{ \overline{AB} }[/math] 위에 있음이 증명되었다.

관련 항목

• 다각형
• 원 (도형)
• 공원점
• 톨레미의 정리