쌍곡 기하학

쌍곡 기하학(雙曲幾何學, Hyperbolic Geometry)은 기하학의 한 분류로, 타원 기하학과 함께 비유클리드 기하학 중에서는 제일 잘 알려진 기하학이다. 일반인들에게 쌍곡 기하학을 설명할 때 흔히 "오목한 면에서 정의되는 기하학"라고들 하는데, 그다지 정확한 설명은 아니다. 타원 기하학(Elliptic Geometry)가 타원체(Ellipsoid) 위에서 정의되는 기하학이듯이, 쌍곡 기하학(Hyperbolic Geometry)는 쌍곡면(Hyperboloid) 위에서 정의되는 기하학이다. 수식으로는 [math]\displaystyle{ \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=\pm1 }[/math]의 형태다.

타원 기하학이 유클리드 기하학의 지식만 있어도 이해할 수 있는 것과 달리, 쌍곡 기하학은 유클리드 기하학은 물론, 절대 기하학, 사영 기하학, 복소평면, 군, 선형대수학, 미적분학 등등의 지식이 필수다. 다행히도 심도있는 레벨로 알고 있을 필요는 없고, 주요 개념만 알고 있으면 된다.

모델

쌍곡 기하학은 절대 기하학에 속하기 때문에 절대 기하학과 동일한 모델을 기반으로 한다. 절대 기하학에서 평행선 공준을 취한 것이 유클리드 기하학이라면, 쌍곡 기하학은 평행선 공준을 부정한 기하학. 즉, 한 점을 지나고, 다른 직선에 평행한 직선이 2개 이상인 기하학. 일단 쌍곡 기하학에 들어가기 전에 가장 기본적인 사영 기하학을 알고 가자.

설명

사영 기하학

사영 기하학(Projective Geometry)이란, 간단히 설명하면 기하학적 물체를 다른 물체 위에 내려찍는 것을 연구하는 기하학이다. 고등학교 기하와 벡터에서 정사영이라는 것을 배웠다면 이해가 쉽게 될 것이다. 아니라면 사영(射影)이나 Projection의 단어를 잘 생각해보자. 일단 실사영선(Real Projective Line, [math]\displaystyle{ \mathbb{RP}^1 }[/math])에 대해 알아보자.

수학적으로, 서로 평행한 두 선은 만나지 않는다. 그러나 시각적으로, 두 선은 무한한 끝에서 만나는 것처럼 보인다. 이 문제를 해결하기 위해서 도입된 것이 무한대점(Point of Infinity)이며, 실사영선은 일반적인 실수직선에 무한대점을 더한 것이라 생각하면 된다. 집합 기호로 표현하면 [math]\displaystyle{ \mathbb{RP}^1=\mathbb{R}\cup\left\{\infty\right\} }[/math]. 실사영선을 기하학적으로 표현하는 방법엔 크게 두 가지가 있는데, 하나는 그냥 직선, 다른 하나는 원. 여기서는 실사영선을 직선+무한대점으로 생각하기로 한다.

이제, 실사영선을 다른 실사영선 위로 사영시키는 변환을 생각해보자. 이해를 돕기 위해 일단 구체적인 예시를 하나 들겠다.

점 [math]\displaystyle{ P=\left(a,b\right) }[/math]를 [math]\displaystyle{ x }[/math]축을 거쳐 [math]\displaystyle{ y }[/math]축 위로 사영시킨다고 가정하자. 이 사영 함수를 [math]\displaystyle{ f }[/math]라 하고, 거치는 [math]\displaystyle{ x }[/math]축 위의 점을 [math]\displaystyle{ t }[/math]라 하면 도달하는 [math]\displaystyle{ y }[/math]축의 점은 [math]\displaystyle{ f\left(t\right) }[/math]이다. 직선의 기울기가 일정함을 이용하며 식을 세우면, [math]\displaystyle{ \frac{b}{a-t}=-\frac{f\left(t\right)}{t} }[/math]이고, 정리하면 [math]\displaystyle{ f\left(t\right)=\frac{bt}{t-a} }[/math]이다.

일단 위 예시가 실생활에서 뭘 뜻하는지 알고 가자. 일단 점 [math]\displaystyle{ P }[/math]는 우리의 "눈"이다. 그리고 거쳐가는 선(예시에서는 [math]\displaystyle{ x }[/math]축)은 우리가 눈으로 "바라보는 것"이다. 마지막으로 도달하는 선(예시에서는 [math]\displaystyle{ y }[/math]축)은 우리가 바라보는 것이 "비춰지는 곳"이다. 그럼, 눈의 위치에 따라서 우리가 바라보는 물체가 비춰지는 형상이 다름을 쉽게 알 수 있다. 그 달라지는 형상을 표현한 것이 바로 저 함수인 것이다. 뜬금없이 미술 수업

증명은 하지 않겠지만, 위와 같은 사영 변환은 전부 [math]\displaystyle{ f\left(x\right)=\frac{ax+b}{cx+d} }[/math]의 형태를 띠고 있다. 여기서 [math]\displaystyle{ x }[/math]는 [math]\displaystyle{ \mathbb{RP}^1 }[/math]의 원소이며, 함수 [math]\displaystyle{ f }[/math]는 [math]\displaystyle{ \mathbb{RP}^1\to\mathbb{RP}^1 }[/math]인 함수이다. 무한대점의 계산을 어떻게 하냐는 의문이 들 수 있는데, 함수의 극한이라고 생각하면 된다. 즉, [math]\displaystyle{ x=\infty }[/math]이면 [math]\displaystyle{ f\left(x\right)=\frac{a}{c} }[/math]이고, [math]\displaystyle{ x=-\frac{d}{c} }[/math]이면 [math]\displaystyle{ f\left(x\right)=\infty }[/math]이다. 이러한 변환을 선형 분수 변환(Linear Fractional Transformation, LFT)이라 부른다. 모든 LFT는 [math]\displaystyle{ x\mapsto x+l,\,x\mapsto kx\,(k\neq0),\,x\mapsto\frac{1}{x} }[/math]의 적절한 합성으로 이루어진다는 것을 쉽게 알 수 있는데, 저 세 함수를 LFT의 생성함수라고 부른다. 정의역과 공역은 당연히 전부 [math]\displaystyle{ \mathbb{RP}^1 }[/math]. 한편, 저 세 생성함수는 일대일 대응 함수임을 쉽게 보일 수 있다. 일대일 대응 함수의 합성함수도 일대일 대응이므로, 모든 LFT는 일대일 대응 함수라는 사실을 알 수 있다.

사영 변환이 LFT라고 했지만, 모든 LFT가 사영 변환일까? 이를 확인하기 위해서는 LFT의 생성함수가 사영 변환인지 체크하면 된다.

증명 [math]\displaystyle{ x\mapsto x+l }[/math]: 시점을 무한대점으로 한 상태에서, 평행한 두 선에 대한 사영이다. [math]\displaystyle{ x\mapsto kx }[/math]: 시점이 무한대점이 아닌 상태에서, 평행한 두 선에 대한 사영이다. [math]\displaystyle{ x\mapsto\frac{1}{x} }[/math]: 원점에서 [math]\displaystyle{ y=1 }[/math]을 지나 [math]\displaystyle{ x=1 }[/math]에 사영시킨 것이다.

따라서, 사영 변환과 LFT는 동치이다. 사영 변환은 직관적으로 이해하기 힘들기 때문에, 앞으로는 LFT를 생각하자.

LFT가 등거리사상이 아님을 쉽게 알 수 있다. 하지만, LFT는 비조화비(Cross Ratio)라는 것을 보존한다. 한 직선 위의 서로 다른 네 점 [math]\displaystyle{ p,\,q,\,r,\,s }[/math]의 비조화비는 다음과 같이 정의한다.

[math]\displaystyle{ \left[p,q;r,s\right]=\frac{\left(r-p\right)/\left(s-p\right)}{\left(r-q\right)/\left(s-q\right)}=\frac{\left(r-p\right)\left(s-q\right)}{\left(r-q\right)\left(s-p\right)} }[/math]

LFT의 생성함수가 비조화비를 보존한다는 것을 보이면 모든 LFT가 비조화비를 보존한다는 것을 보일 수 있다. 증명은 [math]\displaystyle{ \left[f\left(p\right),f\left(q\right);f\left(r\right),f\left(s\right)\right]=\left[p,q;r,s\right] }[/math]임을 보이면 되는데, 쉬우므로 생략. 이제 비조화비와 LFT에 대한 간단한 성질을 알고 가자.

정리 1

서로 다른 세 점 [math]\displaystyle{ p,\,q,\,r\in\mathbb{RP}^1 }[/math]에 대해, 임의의 [math]\displaystyle{ x\in\mathbb{RP}^1 }[/math]은 [math]\displaystyle{ p,\,q,\,r,\,x }[/math]의 비조화비로 결정된다.

증명 [math]\displaystyle{ \left[p,q;r,x\right]=\left[p,q;r,y\right] }[/math]이라 하자. 양변을 잘 정리하면 [math]\displaystyle{ x=y }[/math]가 나온다. 즉, 세 점과 비조화비가 주어지면, 다른 한 점은 하나로 결정된다.

정리 2

서로 다른 세 점 [math]\displaystyle{ p,\,q,\,r\in\mathbb{RP}^1 }[/math]과 서로 다른 세 점 [math]\displaystyle{ p',\,q',\,r'\in\mathbb{RP}^1 }[/math]에 대해, [math]\displaystyle{ p\mapsto p',\,q\mapsto q',\,r\mapsto r' }[/math]인 LFT가 존재한다.

증명 일반성을 잃지 않고 [math]\displaystyle{ p=p' }[/math]가 되도록 두 [math]\displaystyle{ \mathbb{RP}^1 }[/math]를 잡는다. 이제, 점 [math]\displaystyle{ P }[/math]를 [math]\displaystyle{ \overleftrightarrow{qq'} }[/math]와 [math]\displaystyle{ \overleftrightarrow{rr'} }[/math]의 교점이라 가정하자. 그럼, 찾고자 하는 LFT는 [math]\displaystyle{ P }[/math]를 시점으로, [math]\displaystyle{ p,\,q,\,r }[/math]를 지나는 [math]\displaystyle{ \mathbb{RP}^1 }[/math]를 [math]\displaystyle{ p',\,q',\,r' }[/math]를 지나는 [math]\displaystyle{ \mathbb{RP}^1 }[/math]에 사영시킨 것이다. 참고로 이 정리는 대수적인 방법으로도 쉽게 보일 수 있다.

정리 3

만약 [math]\displaystyle{ f,\,g }[/math]가 [math]\displaystyle{ p,\,q,\,r\mapsto p',\,q',\,r' }[/math]인 LFT라면, [math]\displaystyle{ f=g }[/math]이다.

증명 우선, 정리 2에 의해 조건을 만족하는 LFT가 존재한다. 그런데, 정리 1에 의해 [math]\displaystyle{ f }[/math]와 [math]\displaystyle{ g }[/math]의 비조화비는 항상 같다. 즉, [math]\displaystyle{ f=g }[/math].

LFT와 비조화비는 아래에서 설명할 쌍곡 기하학의 가장 대표적인 모델, 힐베르트 평면에서 쓰이게 된다.

힐베르트 평면

힐베르트 평면이란 쌍곡 기하학의 모델 중에서 가장 많이 쓰이는 모델로서, 다비드 힐베르트의 이름을 땄다. 복소평면 중 위쪽 절반을 사용하며, 독특한 거리 함수를 가지고 있다. 정확한 정의는 다음과 같다.

1. 힐베르트 평면 [math]\displaystyle{ \mathbb{H}^2=\left\{z|\Im\left(z\right)\gt 0\right\} }[/math]
2. 매개변수화 된 경로를 [math]\displaystyle{ \gamma\left(t\right)=\left(x\left(t\right),y\left(t\right)\right)=x\left(t\right)+iy\left(t\right),\,a\leq t\leq b }[/math]라 하자. 그럼, 경로의 길이는
   [math]\displaystyle{ l\left(\gamma\right)=\int_a^b\frac{\left|\gamma'\left(t\right)\right|}{\Im\left(\gamma\left(t\right)\right)}\mathrm{d}t }[/math]로 정의한다.
3. 두 점 사이의 측지선(Geodesic)은 두 점을 잇는 여러 경로 중에서 길이가 제일 짧은 것으로 정의한다.

우선 제일 간단한 경로의 길이를 구해보자.

예시 1

수평선의 길이 [math]\displaystyle{ x+i,\,0\leq x\leq1 }[/math]: [math]\displaystyle{ \int_0^1\frac{1}{1}\mathrm{d}x=1 }[/math] [math]\displaystyle{ x+2i,\,0\leq x\leq1 }[/math]: [math]\displaystyle{ \int_0^1\frac{1}{2}\mathrm{d}x=\frac{1}{2} }[/math] [math]\displaystyle{ x+3i,\,0\leq x\leq1 }[/math]: [math]\displaystyle{ \int_0^1\frac{1}{3}\mathrm{d}x=\frac{1}{3} }[/math] 뭔가 이상하다는 사실을 눈치챘는가? 분명히 우리 눈에는 길이가 같은 수평선인데, 힐베르트 평면에서는 길이가 다르다. 허수부가 커질수록(평면의 위쪽으로 갈 수록) 길이는 점점 짧아지게 되는 것이다. 세 선의 길이를 같게 만드려면 2, 3번 선의 (유클리드) 길이를 각각 2배, 3배로 늘려야 한다. 그럼 이게 실생활에서는 무엇을 의미할까? 바로 원근법이다. 종이에 자로 동일한 길이의 수평선을 몇 개 위로 쌓고, 종이를 책상 위에 눕혀놓고 멀리서 바라보자. 원근법에 의해서 위쪽에 그린 선은 분명히 동일한 길이인데도 불구하고 시각적으로 길이가 짧아보인다. 눈에 보이는 길이를 같게 만드려면 결국 위쪽에 그린 선을 길게 그려야한다. 힐베르트 평면의 길이 재는 방법은 원근법을 보정한 것이라 이해할 수 있다.

예시 2

두 점 사이의 거리 [math]\displaystyle{ P=\left(0,1\right),\,Q=\left(2,1\right) }[/math]이라 하자. 이 두 점을 잇는 첫 번째 경로를 수평선, 두 번째 경로를 ∧모양의 경로라 하자. 예시 1과 같은 방법으로 하면 길이가 2임을 알 수 있다. 우선 ∧모양의 경로를 매개변수화 하자. [math]\displaystyle{ \begin{cases}t+\left(1+t\right)i,&\text{ if }0\leq t\leq1\\t+\left(3-t\right)i,&\text{ if }1\leq t\leq2\end{cases} }[/math] 이제 경로의 길이를 구하자. [math]\displaystyle{ \begin{align}&\int_0^1\frac{\left|1+i\right|}{1+t}\mathrm{d}t+\int_1^2\frac{\left|1-t\right|}{3-t}\mathrm{d}t\\=&\int_0^1\frac{\sqrt2}{1+t}\mathrm{d}t+\int_1^2\frac{\sqrt2}{3-t}\mathrm{d}t\\=&\sqrt2\left[\ln\left|1+t\right|\right]_0^1+\sqrt2\left[-\ln\left|3-t\right|\right]_1^2\\&=2\sqrt2\ln2\approx1.96\lt 2\end{align} }[/math] 놀랍게도, 직선의 길이가 더 길다는 것을 알 수 있다. 직선의 정의가 두 점을 잇는 가장 짧은 경로라는 것을 생각하면, 우리가 아는 직선이 힐베르트 평면에서는 직선이 아닌 것이다. 그렇기 때문에 측지선이라는 용어를 쓰는 것이다.

예시 2를 읽었다면, 쌍곡 기하학에서의 직선(=측지선)이 무엇인지 의문이 갈 것이다. 수평선은 직선이 아니지만, 다행히 수직선은 직선이다. 생각해보면 당연한데, 힐베르트 평면에서는 수직 위로 갈 수록 길이가 짧아지고 수평 좌우는 길이를 줄이는데 아무런 도움이 되지 않는다. 그렇기 때문에 수직선은 가장 짧은 길이고, 이는 곧 수직선이 측지선이라는 사실을 의미한다. 수직선의 길이는 다음과 같다.

[math]\displaystyle{ \gamma\left(t\right)=x+ti,\,a\leq t\leq b }[/math], [math]\displaystyle{ l\left(\gamma\right)=\int_a^b\frac{1}{t}\mathrm{d}t=\ln\frac{b}{a} }[/math]

힐베르트 평면의 측지선

그럼 수평 거리는 어떻게 재야 최소일까? 증명은 하지 않겠지만, 중심이 실수축 위에 있는 반원이 바로 찾고자 하는 선이다. 정리하면, 쌍곡 기하학에서의 측지선은 수직선과 중심이 실수축 위에 있는 반원이다. 앞으로 특별한 말이 없으면 "직선=측지선"이라 생각하자.

등거리 사상

힐베르트 평면에서 거리를 구하는 방법과 측지선에 대해 이해했다면, 다음 단계는 당연히 힐베르트 평면에서의 등거리 사상을 아는 것이다. 우선 가장 대표적인 등거리 사상 몇 가지를 알아보자.

1. [math]\displaystyle{ f\left(z\right)=z+l,\,l\in\mathbb{R} }[/math]: 실수축 방향으로 이동하는 변환이다 (수평 이동). 힐베르트 평면에서 거리에 영향을 끼치는 것은 수직 이동이므로 수평 이동은 거리를 보존함을 쉽게 알 수 있다.
2. [math]\displaystyle{ f\left(z\right)=-\bar{z} }[/math]: 허수축에 대한 대칭 이동이다. 마찬가지로 수직적인 위치 변환은 이루어지지 않기 때문에 거리를 보존한다.
3. [math]\displaystyle{ f\left(z\right)=kz,\,k\gt 0 }[/math]: 원점을 지나는 (유클리드) 직선에 대한 팽창 변환(Dilation)이다. 앞의 2개와는 다르게 수직 이동을 동반하기 때문에 정말로 거리를 보존하는지는 쉽게 확인할 수 없다.

   수직선이 측지선임을 알고, 수직선의 길이는 쉽게 구할 수 있으므로 수직선을 예시로 이 변환이 등거리 사상인지 확인해보자.
   [math]\displaystyle{ d\left(ai,bi\right)=\left|\ln\left(\frac{b}{a}\right)\right|=\left|\ln\left(\frac{kb}{ka}\right)\right|=d\left(kai,kbi\right) }[/math]
   따라서, 팽창 변환은 적어도 수직선의 길이를 보존한다는 확인할 수 있다.

4. [math]\displaystyle{ f\left(z\right)=\frac{1}{\bar{z}} }[/math]: 단위원에 대한 반전 변환(Inversion)이다. 반전이라는 개념이 생소할텐데, 원에 대한 대칭 이동이라고 생각하면 된다. 반전에 대해 더 자세한 것은 반전 기하학 참조.

위 등거리 사상의 특징은 전부 [math]\displaystyle{ \frac{az+b}{cz+d} }[/math]나 [math]\displaystyle{ \frac{a\bar{z}+b}{c\bar{z}+d} }[/math]의 형태로 표현된다는 것이다. 그런데 저 형태를 어디서 많이 보지 않았는가? 바로 LFT다. 이제 [math]\displaystyle{ \mathbb{RP}^1 }[/math]에서 정의되었던 LFT를 [math]\displaystyle{ \mathbb{H}^2 }[/math]로 확장해보자.

정의

힐베르트 평면에서의 선형 분수 변환(LFT)은 함수 [math]\displaystyle{ f:\mathbb{H}^2\to\mathbb{H}^2,\,f\left(z\right)=\frac{az+b}{cz+d},\,a,\,b,\,c,\,d\in\mathbb{R},\,ad-bc\gt 0 }[/math]이다.

왜 저런 온갖 조건들이 붙었는지 의문이 들텐데, 저 조건이 있어야 LFT가 일대일 대응이 되기 때문이다. 이제 그 사실을 증명해보자.

보조 정리

[math]\displaystyle{ \Im\left(f\left(z\right)\right)=\frac{\Im\left(z\right)\left(ad-bc\right)}{\left|cz+d\right|^2} }[/math]

증명 [math]\displaystyle{ f\left(z\right)=\frac{az+b}{cz+d}=\frac{\left(az+b\right)\left(c\bar{z}+d\right)}{\left(cz+d\right)\left(c\bar{z}+d\right)}=\frac{acz\bar{z}+adz+bc\bar{z}+bd}{\left|cz+d\right|^2} }[/math] 그런데 [math]\displaystyle{ acz\bar{z}+bd }[/math]는 실수이므로 [math]\displaystyle{ f\left(z\right) }[/math]의 허수부는 [math]\displaystyle{ adz+bc\bar{z} }[/math]에만 영향을 받는다. 따라서, [math]\displaystyle{ \Im\left(f\left(z\right)\right)=\frac{\Im\left(z\right)\left(ad-bc\right)}{\left|cz+d\right|^2} }[/math]

정리

LFT는 [math]\displaystyle{ ad-bc\gt 0 }[/math]이면 일대일 대응 함수이다. 역으로, LFT가 일대일 대응 함수이면 [math]\displaystyle{ ad-bc\gt 0 }[/math]이다.

증명 먼저 [math]\displaystyle{ ad-bc\gt 0 }[/math]이라 가정하자. 그럼 보조 정리에 의해, [math]\displaystyle{ \Im\left(z\right)\gt 0 }[/math]이면 [math]\displaystyle{ \Im\left(f\left(z\right)\right)\gt 0 }[/math]이기 때문에 [math]\displaystyle{ f:\mathbb{H}^2\to\mathbb{H}^2 }[/math]이다. 이제, [math]\displaystyle{ f\left(z\right)=f\left(w\right) }[/math]이라 가정하자 ([math]\displaystyle{ z,\,w\in\mathbb{H}^2 }[/math]). 양변을 전개하여 잘 정리하면 [math]\displaystyle{ z=w }[/math]라는 사실을 쉽게 알 수 있고, 이는 [math]\displaystyle{ f }[/math]가 일대일 함수라는 사실을 의미한다. 이제, 임의의 [math]\displaystyle{ w\in\mathbb{H}^2 }[/math]를 고르자. 그리고 [math]\displaystyle{ f\left(z\right)=w }[/math]를 풀면 [math]\displaystyle{ z=\frac{wd-b}{a-cw} }[/math]가 나온다. 만약 [math]\displaystyle{ a=c=0 }[/math]이면, [math]\displaystyle{ ad-bc\gt 0 }[/math]이라는 가정에 모순이다. 만약 [math]\displaystyle{ c=0 }[/math]이라면, [math]\displaystyle{ cw=0 }[/math]이고, [math]\displaystyle{ a\neq0 }[/math]이므로 [math]\displaystyle{ a\neq cw }[/math]이다. 반대로, 만약 [math]\displaystyle{ a=0 }[/math]이면, [math]\displaystyle{ c\neq0 }[/math]이고, [math]\displaystyle{ cw\neq0 }[/math]이므로 [math]\displaystyle{ a\neq cw }[/math]이다. 만약 [math]\displaystyle{ a\neq0,\,c\neq0 }[/math]라면, [math]\displaystyle{ cw\in\mathbb{C}\setminus\mathbb{R} }[/math]이고 [math]\displaystyle{ a\in\mathbb{R} }[/math]이므로 [math]\displaystyle{ a\neq cw }[/math]이다. 따라서, [math]\displaystyle{ z }[/math]는 잘 정의되었다. 또한, 보조 정리에 의해 [math]\displaystyle{ \Im\left(z\right)=\frac{\Im\left(w\right)\left(ad-bc\right)}{\left|a-cw\right|^2}\gt 0 }[/math]이므로, [math]\displaystyle{ z\in\mathbb{H}^2 }[/math]이다. 따라서, [math]\displaystyle{ f }[/math]는 전사 함수이다. 역으로, [math]\displaystyle{ ad-bc\leq0 }[/math]이라 가정하자. 그럼 [math]\displaystyle{ f:\mathbb{H}^2\not\to\mathbb{H}^2 }[/math]임을 쉽게 알 수 있다. 이는 곧 [math]\displaystyle{ f }[/math]가 일대일 대응이 아니라는 사실을 의미한다.

LFT에서 만약 [math]\displaystyle{ ad-bc\lt 0 }[/math]이면, 켤레 복소수를 취해 일대일 대응을 만들 수 있다. 그런데 켤레 복소수를 취하는 것 말고는 완전히 동일하므로 [math]\displaystyle{ ad-bc\gt 0 }[/math]으로 항상 가정하자.

한편, [math]\displaystyle{ f\left(z\right)=\frac{az+b}{cz+d}=\frac{raz+rb}{rcz+rd} }[/math]이므로, [math]\displaystyle{ r=\frac{1}{\sqrt{ad-bc}} }[/math]을 취하면 [math]\displaystyle{ ad-bc=1 }[/math]인 동일한 변환을 만들 수 있다. 이러한 변환을 뫼비우스 변환이라고 하는데, [math]\displaystyle{ ad-bc }[/math]의 값이 1이 아니어도 1로 금방 만들어 줄 수 있기 때문에 힐베르트 평면에서의 LFT는 전부 뫼비우스 변환이라 할 수 있다. 다르게 정의하면, [math]\displaystyle{ \mathbb{RP}^1 }[/math]에서의 LFT를 [math]\displaystyle{ \mathbb{H}^2 }[/math]로 확장한 것이 바로 뫼비우스 변환. 확장하는 방법은 다음과 같다.

1. [math]\displaystyle{ ad-bc\gt 0 }[/math]인 경우: [math]\displaystyle{ \frac{ax+b}{cx+d}\to\frac{az+b}{cz+d} }[/math]
2. [math]\displaystyle{ ad-bc\lt 0 }[/math]인 경우: [math]\displaystyle{ \frac{ax+b}{cx+d}\to\frac{a\bar{z}+b}{c\bar{z}+d} }[/math]
3. [math]\displaystyle{ ad-bc=0 }[/math]인 경우는 상수 함수가 되기 때문에 고려하지 않는다.

뫼비우스 변환

몇 가지 뫼비우스 변환이 등거리 사상임을 확인했다. 그런 자연히 드는 의문은 바로 모든 뫼비우스 변환이 등거리 사상인가 일 것이다. 이 의문을 이제 풀어보자.

보조 정리

[math]\displaystyle{ ad-bc=1 }[/math]이라 가정하자. 그럼 [math]\displaystyle{ f\left(z\right)=\frac{az+b}{cz+d} }[/math]에 대해 [math]\displaystyle{ f'\left(z\right)=\frac{1}{\left(cz+d\right)^2} }[/math]이다.

증명 [math]\displaystyle{ f'\left(z\right)=\frac{a\left(cz+d\right)-c\left(az+b\right)}{\left(cz+d\right)^2}=\frac{ac-bc}{\left(cz+d\right)^2}=\frac{1}{\left(cz+d\right)^2} }[/math]

정리

모든 뫼비우스 변환은 등거리 사상이다.

증명 [math]\displaystyle{ \gamma\left(t\right),\,0\leq t\leq1 }[/math]을 힐베르트 평면의 임의의 경로라 가정하자. 그럼, [math]\displaystyle{ l\left(\gamma\left(t\right)\right)=\int_0^1\frac{\left|\gamma'\left(t\right)\right|}{\Im\left(\gamma\left(t\right)\right)}\mathrm{d}t }[/math]이다. 한편,[math]\displaystyle{ f\left(\gamma\left(t\right)\right)=\frac{a\gamma\left(t\right)+b}{c\gamma\left(t\right)+d} }[/math]이므로, [math]\displaystyle{ l\left(f\left(\gamma\left(t\right)\right)\right)=\int_0^1\frac{\left|f\left(\gamma\left(t\right)\right)'\right|}{\Im\left(f\left(\gamma\left(t\right)\right)\right)}\mathrm{d}t=\int_0^1\frac{\left|f'\left(\gamma\left(t\right)\right)\gamma'\left(t\right)\right|}{\Im\left(f\left(\gamma\left(t\right)\right)\right)}\mathrm{d}t=\int_0^1\frac{\frac{1}{\left|c\gamma\left(t\right)+d\right|^2}\left|\gamma'\left(t\right)\right|}{\frac{\Im\left(\gamma\left(t\right)\right)}{\left|c\gamma\left(t\right)+d\right|^2}}\mathrm{d}t=\int_0^1\frac{\left|\gamma'\left(t\right)\right|}{\Im\left(\gamma\left(t\right)\right)}\mathrm{d}t }[/math]이므로, [math]\displaystyle{ l\left(f\left(\gamma\left(t\right)\right)\right)=l\left(\gamma\left(t\right)\right) }[/math]이다. 따라서, 뫼비우스 변환은 경로의 길이를 보존한다.

앞서, [math]\displaystyle{ ad-bc\lt 0 }[/math]인 경우에는 켤레 복소수를 취해 뫼비우스 변환을 얻는다고 하였다. 이 경우에도, 같은 증명 방법을 이용해서 일대일 대응이라는 것과 등거리 사상이라는 것을 보일 수 있다. 그러면, 정의역을 조금 더 확장하여 뫼비우스 변환을 다시 정의할 수 있다.

정의

뫼비우스 변환이란, [math]\displaystyle{ f\left(z\right)=\frac{az+b}{cz+d},\,a,\,b,\,c,\,d\in\mathbb{R},\,ad-bc\neq0 }[/math]인 함수를 말한다. 정의역과 치역은 [math]\displaystyle{ \mathbb{C}\cup\left\{\infty\right\} }[/math]이며, [math]\displaystyle{ f\left(-\frac{d}{c}\right)=\infty,\,f\left(\infty\right)=\frac{a}{c} }[/math]로 정의한다. 한편, [math]\displaystyle{ ad-bc\gt 0 }[/math]이면 방향을 보존한다고 하며(Orientation Preserving), [math]\displaystyle{ ad-bc\lt 0 }[/math]이면 방향을 뒤집는다고 한다(Orientation Reversing).

편의상, 앞으로는 방향을 보존하는 뫼비우스 변환만을 다루기로 한다. 이제, 뫼비우스 변환의 간단한 성질을 알아보자.

성질 1

뫼비우스 변환의 역함수도 뫼비우스 변환이다.

증명 [math]\displaystyle{ f\left(z\right)=\frac{az+b}{cz+d} }[/math]의 역함수가 [math]\displaystyle{ g\left(w\right)=\frac{dw-b}{-cw+a} }[/math]임은 쉽게 알 수 있다. 역함수 역시 방향을 보존한다는 사실도 같이 알 수 있다.

성질 2

두 뫼비우스 변환의 합성함수도 뫼비우스 변환이다.

증명 [math]\displaystyle{ f\left(z\right)=\frac{az+b}{cz+d},\,g\left(z\right)=\frac{ez+f}{gz+h} }[/math]라 하자. 그럼, [math]\displaystyle{ f\circ g\left(z\right)=\frac{\left(ae+bg\right)z+\left(af+bh\right)}{\left(ce+dg\right)z+\left(cf+bd\right)} }[/math]이다. 즉, 합성함수도 뫼비우스 변환이다. 또한, 방향을 보존한다는 사실도 같이 알 수 있다.

혹시 뫼비우스 변환의 역함수와 합성함수가 행렬과 같다는 것을 눈치챈 사람이 있는가? [math]\displaystyle{ f\left(z\right)=\frac{az+b}{cz+d} }[/math]을 [math]\displaystyle{ \begin{bmatrix}a&&b\\c&&d\end{bmatrix} }[/math]로 나타내면, 역함수는 [math]\displaystyle{ \begin{bmatrix}d&&-b\\-c&&a\end{bmatrix} }[/math]가 되는데, 이는 원래 행렬의 역행렬과 동일하다! 합성 함수 역시 두 행렬의 곱임을 쉽게 알 수 있다. 그럼, 뫼비우스 변환의 집합과 행렬의 집합 사이에 사상을 하나 정의할 수 있다.

[math]\displaystyle{ \phi:GL\left(2,\mathbb{R}\right)\to\left\{\right. }[/math]뫼비우스 변환[math]\displaystyle{ \left.\right\} }[/math], [math]\displaystyle{ \begin{bmatrix}a&&b\\c&&d\end{bmatrix}\mapsto\frac{az+b}{cz+d} }[/math]

한편, 합성함수가 행렬의 곱과 같다는 사실을 확인했으므로, [math]\displaystyle{ \phi\left(AB\right)=\phi\left(A\right)\phi\left(B\right) }[/math]이고, 이는 곧 저 사상이 준동형사상임을 의미한다. 또한, 저 사상이 전사 함수임은 자명하다. 따라서, 동형 사상 정리에 의해 [math]\displaystyle{ GL\left(2,\mathbb{R}\right)/\ker\phi\cong\left\{\right. }[/math]뫼비우스 변환[math]\displaystyle{ \left.\right\} }[/math]이다. 이제 핵을 찾아야 하는데, 핵이 [math]\displaystyle{ xI }[/math]임을 쉽게 보일 수 있다. 즉, 뫼비우스 변환의 집합은 (곱하는 상수를 무시한) 행렬의 집합과 동형이라는 것을 알 수 있다. 이는 곧 뫼비우스 변환을 행렬로 변환하여 생각해줄 수 있다는 것을 의미한다.

뫼비우스 변환에 대해 마지막으로 알아야할 것은, 측지선이 어떻게 변환되냐이다. 이를 알기 전에 측지선의 특징을 하나 알고 가자.

정리

측지선은 [math]\displaystyle{ Az\bar{z}+B\left(z+\bar{z}\right)+C=0 }[/math]의 형태를 가지고 있다. 반대로, 이 형태를 가지고 있으면 측지선이다.

증명 측지선이 수직선과 반원인 것은 이미 설명했다. 수직선은 [math]\displaystyle{ z+\bar{z}=k }[/math]의 형태이며, 반원은 [math]\displaystyle{ \left|z-c\right|=r }[/math]의 형태이다. 수직선은 이미 보이고자 하는 형태이므로, 반원만 체크해주면 된다. 우선, 양변을 제곱하면, [math]\displaystyle{ \left(z-c\right)\left(\bar{z}-c\right)=r^2 }[/math]이고, 정리하면 원하는 형태라는 것을 쉽게 확인할 수 있다. 역으로, [math]\displaystyle{ Az\bar{z}+B\left(z+\bar{z}\right)+C=0 }[/math]의 형태를 가진 선이 존재한다고 가정하자. 만약 [math]\displaystyle{ A=0 }[/math]이면, 저 선은 수직선이고, 수직선은 곧 측지선이다. 만약 [math]\displaystyle{ A\neq0 }[/math]이면, [math]\displaystyle{ z\bar{z}+\frac{B}{A}\left(z+\bar{z}\right)=-\frac{C}{A} }[/math]이다. [math]\displaystyle{ -\frac{B}{A}=c,\,r^2=-\frac{C}{A}+\frac{B^2}{A^2} }[/math]로 정의하면, 주어진 식은 [math]\displaystyle{ \left|z-c\right|=r }[/math]이 되는 것을 쉽게 확인할 수 있다. 만약 [math]\displaystyle{ r^2\lt 0 }[/math]이라면, 공집합이 된다.

이제, 뫼비우스 변환의 생성함수를 알아보자.

1. [math]\displaystyle{ f:z\mapsto z+l }[/math]
2. [math]\displaystyle{ f:z\mapsto kz,\,k\gt 0 }[/math]
3. [math]\displaystyle{ f:z\mapsto-\frac{1}{z} }[/math]
4. [math]\displaystyle{ f:z\mapsto-\bar{z} }[/math]

방향을 보존하는 뫼비우스 변환은 1, 2, 3으로 쉽게 만들 수 있고, 방향을 뒤집는 뫼비우스 변환은 4를 한 번 끼얹어 주면 된다는 것을 쉽게 알 수 있다. 이제, 뫼비우스 변환이 측지선을 어떻게 바꾸는지 알아보자.

정리

뫼비우스 변환은 측지선을 측지선으로 옮긴다.

증명 [math]\displaystyle{ Az\bar{z}+B\left(z+\bar{z}\right)+C=0 }[/math]에 네 가지 생성함수를 끼얹은 뒤, 같은 형태인지 확인하면 된다. 더이상의 자세한 증명은 생략한다. 한 가지 특이한 점은, 1, 2, 4번 생성함수는 수직선은 수직선으로, 반원은 반원으로 바꾸지만, 3번 생성함수만은 수직선과 반원을 뒤바꾼다.

여기까지 이해했으면, 드디어 힐베르트 평면에서 두 점 사이의 최단 거리를 구할 수 있다.

두 점 사이의 거리

수직선 상에 있는 두 점의 거리를 구하는 방법은 이미 알고 있으므로 문제가 되는 것은 수직선 상에 있지 않은 두 점의 거리이다. 만약 두 점을 거리를 보존하면서 수직선 상에 놓을 수 있다면 거리를 구하는 것은 식은 죽 먹기. 그런데 마침 뫼비우스 변환이 등거리 사상임을 보였으니, 뫼비우스 변환을 어떻게 잘 이용하면 될 것 같지 않은가? 힐베르트 평면에 있는 임의의 두 점의 거리를 구하는 방법은 다음과 같은 과정을 거친다.

1. 만약 두 점이 수직 위아래로 존재한다면, 거리는 [math]\displaystyle{ \left|\ln\left(b/a\right)\right| }[/math]이다.
2. 아니라면, 우선 두 점을 지나는 측지선을 찾는다. 두 점이 수직선 상에 존재하지 않으므로 측지선은 중심이 실수축 위에 있는 반원이다.
3. 측지선의 양 끝점의 좌표를 구한다. 끝점이란, 측지선과 실수축이 만나는 점을 말한다.
4. 이제 찾은 측지선을 허수축으로 변환할 것이다. 양 끝점 중 하나를 0으로, 다른 점을 [math]\displaystyle{ \infty }[/math]로 보내는 뫼비우스 변환을 하나 찾는다. 뫼비우스 변환은 측지선을 측지선으로 변환시키는데, 양 끝점이 수직 위아래에 있다면 그 측지선은 수직선이 된다.
5. 거리를 구하고자 하는 두 점을 뫼비우스 변환에 때려 넣는다.
6. 변환된 두 점은 허수축 위에 존재하므로, 거리를 쉽게 구할 수 있다. 그런데 뫼비우스 변환은 등거리 사상이므로, 찾은 거리가 우리가 찾고자 하는 거리이다.

말로만 들어서는 무슨 소린지 모를 것이기 때문에, 한 가지 예시를 들어 거리를 직접 구해보자. 두 점, [math]\displaystyle{ A=1+i,\,B=3+i }[/math]이 주어졌고, 이 두 점 사이의 거리를 구하고 싶다고 하자. 우선, 이 두 점은 수직선 상에 존재하지 않기 때문에, 뫼비우스 변환을 통해서 수직선 상에 존재하게 만들어 줘야 한다. 일단 제일 먼저 측지선을 찾자.

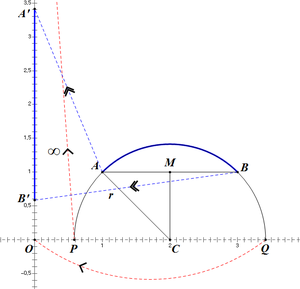
원의 중심에서 현에 내린 수선의 발은 현을 이등분 한다는 것을 중학교 때 배워서 알고 있을 것이다. 이를 역으로 이용하면, 현 [math]\displaystyle{ \overline{AB} }[/math]의 수직이등분선이 실수축과 만나는 점이 찾고자 하는 반원의 중심이라는 것을 알 수 있다. 두 점의 좌표는 [math]\displaystyle{ A=\left(1,1\right),\,B=\left(3,1\right) }[/math]이므로, 중점의 좌표는 [math]\displaystyle{ M=\left(2,1\right) }[/math]이고, 중점에서 현에 수선을 그어 실수축과 만나는 점을 찾으면 반원의 중심 [math]\displaystyle{ C=\left(2,0\right) }[/math]을 찾을 수 있다. 이제 원의 반지름을 찾아야 하는데, 반지름은 [math]\displaystyle{ \overline{CA} }[/math]의 유클리드 길이를 찾으면 된다. 그러면, 찾고자하는 측지선의 방정식은 [math]\displaystyle{ \left|z-2\right|=\sqrt2 }[/math]임을 알 수 있다.

이제 측지선을 허수축으로 변환시켜줘야 한다. 우선, 측지선의 양 끝점을 찾으면, [math]\displaystyle{ P=2-\sqrt2,\,Q=2+\sqrt2 }[/math]이다. 이제 이 양 끝점을 0과 [math]\displaystyle{ \infty }[/math]로 보내주는 뫼비우스 변환을 하나 찾으면 되는데, 가장 간단한 것이 [math]\displaystyle{ f\left(z\right)=\frac{z-\left(2+\sqrt2\right)}{z-\left(2-\sqrt2\right)} }[/math]이다. 그림에도 나와있듯이, [math]\displaystyle{ f }[/math]는 [math]\displaystyle{ P\mapsto\infty,\,Q\mapsto0 }[/math]의 변환을 한다.

뫼비우스 변환을 찾았다면, 두 점 [math]\displaystyle{ A,\,B }[/math]를 [math]\displaystyle{ f }[/math]에 넣자. 그럼, [math]\displaystyle{ f\left(A\right)=A'=\frac{2i}{2-\sqrt2} }[/math]와 [math]\displaystyle{ f\left(B\right)=B'=\frac{2i}{2+\sqrt2} }[/math]를 찾을 수 있다. 그런데 [math]\displaystyle{ f }[/math]는 등거리 사상이므로, 찾고자 하는 길이(푸른색 호 [math]\displaystyle{ \overset{\frown}{AB} }[/math])와 수직선의 길이(푸른색 수직선 [math]\displaystyle{ \overline{A'B'} }[/math])는 같다. 따라서, [math]\displaystyle{ d\left(A,B\right)=d\left(A',B'\right)=\left|\ln\left(\frac{2}{2+\sqrt2}\right)/\left(\frac{2}{2-\sqrt2}\right)\right|=\ln\left(\frac{2+\sqrt2}{2-\sqrt2}\right) }[/math]이다.

등거리 사상의 종류

다음에 할 것은 힐베르트 평면 모델에 존재하는 등거리 사상을 분류하는 것이다. 우선, 우리는 모든 뫼비우스 변환이 등거리 사상임을 알고 있다. 신기하게도 이 명제의 역도 성립하는데, 증명은 등거리 사상이 각도를 보존한다는 사실을 이용한다. 일단 등거리 사상이 각도를 보존한다는 것부터 보이자.

보조 정리

등거리 사상은 각도를 보존한다.

증명 임의의 두 벡터 [math]\displaystyle{ \vec{a},\vec{b} }[/math]가 주어졌다고 하자. 그럼, 이 두 벡터 사이의 각도는 [math]\displaystyle{ \cos\theta=\frac{\vec{a}\cdot\vec{b}}{\left\|a\right\|\left\|b\right\|} }[/math]로 정의된다. 그런데 등거리 사상은 우변의 모든 값을 보존하므로, 좌변의 값도 보존된다. 이는 곧 각도가 보존됨을 의미한다.

정리

힐베르트 평면에서, 모든 등거리 사상은 뫼비우스 변환이다.

증명 임의의 등거리 사상 [math]\displaystyle{ A\left(z\right):\mathbb{H}^2\to\mathbb{H}^2 }[/math]가 있다고 가정하자. [math]\displaystyle{ A }[/math]가 등거리 사상이므로, 서로 다른 세 점 [math]\displaystyle{ i,2i,\frac{1+\sqrt3i}{2} }[/math]은 서로 다른 세 점 [math]\displaystyle{ A\left(i\right),A\left(2i\right),A\left(\frac{1+\sqrt3i}{2}\right) }[/math]으로 변환된다. 한편, 등거리 사상은 측지선을 측지선으로 변환시키므로, [math]\displaystyle{ i,2i }[/math]를 지나는 측지선(허수축)은 [math]\displaystyle{ A\left(i\right),A\left(2i\right) }[/math]을 지나는 유일한 측지선으로 변환된다. 마찬가지로, [math]\displaystyle{ i,\frac{1+\sqrt3i}{2} }[/math]를 지나는 측지선(단위원)도 [math]\displaystyle{ A\left(i\right),A\left(\frac{1+\sqrt3i}{2}\right) }[/math]을 지나는 유일한 측지선으로 변환된다. 한편, 허수축과 단위원은 [math]\displaystyle{ i }[/math]에서 직교하므로, 변환된 두 측지선은 [math]\displaystyle{ A\left(i\right) }[/math]에서 직교한다. 한편, 허수축의 양 끝점은 [math]\displaystyle{ 0,\infty }[/math]이고, 단위원의 한 끝점은 [math]\displaystyle{ 1 }[/math]이며, 등거리 사상은 끝점을 끝점으로 변환시킨다. 즉, [math]\displaystyle{ A\left(0\right),A\left(\infty\right),A\left(1\right) }[/math]은 변환된 측지선의 끝점이다. 이제, [math]\displaystyle{ A\left(0\right)=p,A\left(\infty\right)=q,A\left(1\right)=r }[/math]이라 하자. 비조화비의 성질에 의해, [math]\displaystyle{ p,q,r\mapsto0,\infty,1 }[/math]인 유일한 뫼비우스 변환 [math]\displaystyle{ f }[/math]를 찾을 수 있다. 그러면, [math]\displaystyle{ f\circ A }[/math]는 [math]\displaystyle{ 0,\infty,1 }[/math]를 고정시킨다. 만약 [math]\displaystyle{ f\circ A=id }[/math]임을 보일 수 있다면, [math]\displaystyle{ A=f^{-1} }[/math]이고, 뫼비우스 변환의 역함수도 뫼비우스 변환이므로 증명이 끝난다. 우선, [math]\displaystyle{ f\circ A }[/math]는 허수축의 양 끝점 [math]\displaystyle{ 0,\infty }[/math]를 고정시키므로, 허수축 전체를 고정시킨다는 것을 알 수 있다. 한편, 단위원은 [math]\displaystyle{ \frac{i}{2},2i }[/math]을 양 끝점으로 가지는 선분을 수직이등분한다. 그런데 [math]\displaystyle{ f\circ A }[/math]는 등거리 사상이고, 각도를 보존하는 데다가 허수축을 고정시키므로, 선분을 같은 허수축 위의 어딘가로 변환시킨다. 단위원은 변환된 선분의 수직이등분선으로 변환되는데, [math]\displaystyle{ f\circ A }[/math]는 단위원의 한 끝점인 1을 고정시킨다. 이는 곧 [math]\displaystyle{ f\circ A }[/math]가 단위원을 고정시킨다는 것을 의미하고, 단위원과 허수축의 교점인 [math]\displaystyle{ i }[/math] 역시 고정된다. 마찬가지 방법으로, [math]\displaystyle{ f\circ A }[/math]가 허수축과 단위원의 모든 점을 고정함을 보일 수 있다. 이제, 힐베르트 평면의 임의의 점을 잡자. 이 점은 [math]\displaystyle{ i,2i,\frac{1+\sqrt3i}{2} }[/math]와의 거리로 유일하게 결정되는데, [math]\displaystyle{ f\circ A }[/math]는 저 세 점을 고정시키므로, 세 거리 역시 고정시킴을 알 수 있다. 이는 곧 [math]\displaystyle{ f\circ A }[/math]가 임의의 점을 고정시킴을 의미하고, 곧 [math]\displaystyle{ f\circ A=id }[/math]이다. 따라서, 모든 등거리 사상은 뫼비우스 변환이다.

힐베르트 평면에서의 등거리 사상이 전부 뫼비우스 변환임을 알았으므로, 뫼비우스 변환을 분류하면 등거리 사상을 분류할 수 있다. 그런데 뫼비우스 변환은 [math]\displaystyle{ GL\left(2,\mathbb{R}\right)/xI }[/math]와 동형이므로, 행렬식의 값이 1인 행렬을 대신 분석해도 된다. 자세한 과정은 생략하고, 분류 결과만을 말하면 다음과 같다.

임의의 뫼비우스 변환 [math]\displaystyle{ f\left(z\right)=\frac{az+b}{cz+d} }[/math]를 행렬 [math]\displaystyle{ A=\begin{bmatrix}a&&b\\c&&d\end{bmatrix} }[/math]로 생각하자.

1. 쌍곡 변환 (Hyperbolic): [math]\displaystyle{ A }[/math]가 대각화 가능할 때. [math]\displaystyle{ A\sim B=\begin{bmatrix}k&&0\\0&&1/k\end{bmatrix} }[/math]이며, [math]\displaystyle{ \left|Tr\left(B\right)\right|\gt 2 }[/math]이다.
2. 포물선 변환 (Parabolic): [math]\displaystyle{ A }[/math]가 대각화 가능하지 않으며, 두 고유값이 같을 때. [math]\displaystyle{ A\sim B=\begin{bmatrix}1&&l\\0&&1\end{bmatrix} }[/math]이며, [math]\displaystyle{ \left|Tr\left(B\right)\right|=2 }[/math]이다.
3. 타원 변환 (Elliptic): [math]\displaystyle{ A }[/math]가 대각화 가능하지 않으며, 두 고유값이 다를 때. [math]\displaystyle{ A\sim B=\begin{bmatrix}\cos\theta&&-\sin\theta\\\sin\theta&&\cos\theta\end{bmatrix} }[/math]이며, [math]\displaystyle{ \left|Tr\left(B\right)\right|\lt 2 }[/math]이다.

임의의 뫼비우스 변환이 주어졌을 때, 그게 어떤 종류의 변환인지 찾기 위해서는 일단 행렬로 치환하고 행렬식의 값이 1이 되도록 앞에 계수를 곱해 준다. 그후 대각합을 구하여 2와 비교하면 종류를 알 수 있다. 행렬식의 값이 1이 아니면 변환을 제대로 분석할 수 없으니 주의. 이제 각 변환에 대해 자세히 알아보자.

쌍곡 변환

행렬식의 값이 2보다 크거나 -2보다 작은 변환이고, 전부 [math]\displaystyle{ \begin{bmatrix}k&&0\\0&&1/k\end{bmatrix} }[/math]와 닮았다. 이 행렬을 다시 뫼비우스 변환으로 치환하면 [math]\displaystyle{ f\left(z\right)=k^2z }[/math]인데, 이 변환은 힐베르트 평면의 경계선에 존재하는 0과 [math]\displaystyle{ \infty }[/math]를 고정함을 쉽게 알 수 있다. 0과 [math]\displaystyle{ \infty }[/math]를 지나는 축지선은 허수축인데, 허수축 위의 점은 같은 허수축 위의 점의 다른 곳으로 이동된다는 사실도 알 수 있다. 즉, 이 변환은 허수축을 집합 전체로서 고정시킨다. 이를 일반화하면, 쌍곡 변환은 [math]\displaystyle{ \partial\mathbb{H}^2 }[/math] 위의 두 점을 고정한다고 할 수 있다. 이 때, 두 고정점을 지나는 축지선을 변환의 축(Axis)이라고 부른다. 축 위의 점은 축을 따라서 변환되기 때문. 한 가지 예시를 들어보자.

-1과 1을 고정하는 뫼비우스 변환을 찾아라.

풀이 우선, -1과 1은 힐베르트 평면의 경계선에 존재하므로 찾고자 하는 뫼비우스 변환은 쌍곡 변환이다. 우선, [math]\displaystyle{ g\left(z\right)\leftrightarrow\begin{bmatrix}2&&0\\0&&1/2\end{bmatrix} }[/math]을 생각하자. 그럼, [math]\displaystyle{ g }[/math]는 0과 [math]\displaystyle{ \infty }[/math]를 고정하는 쌍곡 변환이다. 그런데 모든 쌍곡 변환은 서로 닮았으므로, [math]\displaystyle{ g }[/math]에 -1과 1을 0과 [math]\displaystyle{ \infty }[/math]로 보내주는 뫼비우스 변환에 대한 켤레를 취하면 -1과 1을 고정시키는 쌍곡 변환을 얻을 수 있다. 즉, [math]\displaystyle{ T\left(z\right)=\frac{-z-1}{z-1} }[/math]에 대해 [math]\displaystyle{ T^{-1}\circ g\circ T }[/math]를 계산하면 끝이라는 소리. 직접 합성하기에는 계산이 귀찮으므로 행렬을 이용하자. [math]\displaystyle{ T^{-1}\circ g\circ T=\begin{bmatrix}-1&&1\\-1&&-1\end{bmatrix}\begin{bmatrix}2&&0\\0&&1/2\end{bmatrix}\begin{bmatrix}-1&&-1\\1&&-1\end{bmatrix}=\frac{1}{2}\begin{bmatrix}5&&3\\3&&5\end{bmatrix} }[/math]이므로, [math]\displaystyle{ \frac{5z+3}{3z+5} }[/math]가 찾고자 하는 변환이다. 한편, [math]\displaystyle{ \begin{bmatrix}5&&3\\3&&5\end{bmatrix} }[/math]의 행렬식의 값은 16인데, 행렬 전체를 [math]\displaystyle{ \sqrt16=4 }[/math]로 나눠주면 [math]\displaystyle{ \begin{bmatrix}5/4&&3/4\\3/4&&5/4\end{bmatrix} }[/math]가 된다. 이 행렬은 행렬식의 값이 1이며, 대각합이 2.5로, 2보다 크므로 쌍곡 변환이 맞다는 것을 확인할 수 있다.

포물선 변환

행렬식의 값이 2 또는 -2인 변환이며, 전부 [math]\displaystyle{ \begin{bmatrix}1&&l\\0&&1\end{bmatrix} }[/math]와 닮았다. 여기서, [math]\displaystyle{ l\neq0 }[/math]이다. 이 행렬을 뫼비우스 변환으로 치환하면 [math]\displaystyle{ f\left(z\right)=z+l }[/math]인데, 이 변환은 [math]\displaystyle{ \partial\mathbb{H}^2 }[/math]에 존재하는 [math]\displaystyle{ \infty }[/math]를 고정시킨다. 이를 일반화하면, 포물선 변환은 [math]\displaystyle{ \partial\mathbb{H}^2 }[/math] 위의 점 하나를 고정하는 변환이라고 할 수 있다. 고정점을 제외한 다른 점들은 고정점을 접점으로 하는 호로사이클(Hyrocycle)을 따라 변환된다. 한 가지 예시를 들어보자.

0을 고정시키는 뫼비우스 변환을 찾아라.

풀이 0은 경계선 위의 점이므로, 찾고자 하는 변환은 포물선 변환이다. 이제, [math]\displaystyle{ g\left(z\right)=z+1 }[/math]이라 하고, [math]\displaystyle{ T }[/math]를 [math]\displaystyle{ 0\mapsto\infty }[/math]인 뫼비우스 변환이라 하자. 그러면, [math]\displaystyle{ g }[/math]는 [math]\displaystyle{ \infty }[/math]를 고정시키므로, [math]\displaystyle{ T^{-1}\circ g\circ T }[/math]는 0을 고정시키게 된다. [math]\displaystyle{ T=\frac{1}{-z} }[/math]라 하면 모든 요소가 갖춰졌다. 계산은 역시 행렬을 이용한다. [math]\displaystyle{ T^{-1}\circ g\circ T=\begin{bmatrix}0&&-1\\1&&0\end{bmatrix}\begin{bmatrix}1&&1\\0&&1\end{bmatrix}\begin{bmatrix}0&&-1\\1&&0\end{bmatrix}=\begin{bmatrix}-1&&0\\1&&-1\end{bmatrix} }[/math]이므로, [math]\displaystyle{ \frac{-z}{z-1} }[/math]이 찾고자 하는 변환이다. 한편, 마지막 행렬은 행렬식의 값이 1이고, 대각합이 -2이므로 포물선 변환이 맞다는 것을 확인할 수 있다.

타원 변환

행렬식의 값이 -2에서 2사이(0 제외)인 변환이며, 전부 [math]\displaystyle{ \begin{bmatrix}\cos\theta&&-\sin\theta\\\sin\theta&&\cos\theta\end{bmatrix} }[/math]와 닮았다. 이 행렬은 힐베르트 평면 내부의 한 점을 고정시킨다. 가장 많이 쓸 타원 변환은 바로 [math]\displaystyle{ \frac{z-1}{z+1} }[/math]로, 이 변환은 [math]\displaystyle{ i }[/math]를 고정시킨다. 그런데 저 행렬을 어디서 많이 보지 않았는가? 바로 회전 변환 행렬이다. 고정점을 제외한 다른 점들은 고정점을 중심으로 [math]\displaystyle{ -2\theta }[/math]만큼 회전 변환된다. 왜 [math]\displaystyle{ \theta }[/math]가 아니고 [math]\displaystyle{ -2\theta }[/math]인지는 나중에 증명하도록 하고 지금은 그냥 받아들이자.

3+2i를 고정시키는 뫼비우스 변환을 찾아라.

풀이 3+2i는 힐베르트 평면 내부의 점이므로, 찾고자 하는 변환은 타원 변환이다. 한편, [math]\displaystyle{ g\left(z\right)=\frac{z-1}{z+1} }[/math]은 [math]\displaystyle{ i }[/math]를 고정시키는 타원변환이므로, [math]\displaystyle{ T:3+2i\mapsto i }[/math]를 찾은 뒤 [math]\displaystyle{ T^{-1}\circ g\circ T }[/math]를 계산해주면 끝. 조건을 만족시키는 [math]\displaystyle{ T }[/math]는 [math]\displaystyle{ \frac{z-3}{2} }[/math]이다. 이제, 행렬을 이용하여 계산하자. [math]\displaystyle{ T^{-1}\circ g\circ T=\begin{bmatrix}2&&3\\0&&1\end{bmatrix}\begin{bmatrix}1&&-1\\1&&1\end{bmatrix}\begin{bmatrix}1&&-3\\0&&2\end{bmatrix}=\begin{bmatrix}5&&-13\\1&&-1\end{bmatrix} }[/math]이므로, [math]\displaystyle{ \frac{5z-13}{z-1} }[/math]이 찾고자 하는 변환이다. 한편, 마지막 행렬을 정규화시킨 다음에 대각합을 구하면 약 1.4로 2보다 작다는 것을 알 수 있다.

3대칭 정리

유클리드 기하학과 타원 기하학에서, 모든 등거리 사상은 많아야 3개의 대칭 변환의 합성으로 나타낼 수 있다는 것이 알려져 있다. 이를 3대칭 정리라 부르는데, 이 3대칭 정리는 힐베르트 평면 위에서도 그대로 성립한다. 대칭 변환은 방향을 뒤집는 뫼비우스 변환이라 위쪽에서는 사용하지 않았지만, 여기서는 쓰인다. 우선 3대칭 정리를 증명하는데 필요한 대합(Involution)을 정의하자.

함수 [math]\displaystyle{ f:X\to X }[/math]가 [math]\displaystyle{ f^2=id }[/math]를 만족하면 (즉, 역함수가 자기 자신이면), [math]\displaystyle{ f }[/math]를 대합이라고 부른다.

아래에 나오는 LFT는 뫼비우스 변환이 아니라 [math]\displaystyle{ \mathbb{RP}^1 }[/math]의 변환임에 주의하자.

보조 정리 1

[math]\displaystyle{ p,q,r,s }[/math]를 [math]\displaystyle{ q,p,s,r }[/math]로 대응시키는 LFT가 존재한다.

증명 먼저, [math]\displaystyle{ \left[p,q;r,s\right]=\left[q,p;s,r\right] }[/math]임에 주목하자. 비조화비의 성질에 의해, [math]\displaystyle{ p,q,r\mapsto q,p,s }[/math]인 LFT가 존재한다. 그런데 두 비조화비가 같으므로, 이 LFT는 [math]\displaystyle{ s\mapsto r }[/math]이다.

보조 정리 2

[math]\displaystyle{ g }[/math]가 두 점을 서로 교환하는 LFT이면, [math]\displaystyle{ g }[/math]는 대합이다.

증명 [math]\displaystyle{ f\left(p\right)=q,f\left(q\right)=p }[/math]라 가정하자. 또한, [math]\displaystyle{ r }[/math]을 [math]\displaystyle{ f\left(r\right)\neq r }[/math]인 값이라 가정하자. 만약 이런 값이 없다면 [math]\displaystyle{ f }[/math]는 대합이다. 이제, [math]\displaystyle{ f\left(r\right)=s }[/math]이라 하자. LFT는 일대일 대응이므로, [math]\displaystyle{ p,q,r,s }[/math]는 전부 다른 값이다. 이제, [math]\displaystyle{ g }[/math]를 [math]\displaystyle{ p,q,r,s\mapsto q,p,s,r }[/math]인 LFT라 하자. 그러면, 비조화비의 성질에 의해 [math]\displaystyle{ f=g }[/math]임을 수비게 알 수 있다. 따라서, [math]\displaystyle{ f^2\left(r\right)=f\left(s\right)=g\left(s\right)=r }[/math]이고, 이는 곧 [math]\displaystyle{ f^2=id }[/math]임을 의미한다.

보조 정리 3

[math]\displaystyle{ p,q,r\in\mathbb{RP}^1 }[/math]에 대해, [math]\displaystyle{ p,q }[/math]는 교환하고 [math]\displaystyle{ r }[/math]은 고정시키는 대합이 존재한다.

증명 비조화비의 성질에 의해 [math]\displaystyle{ p,q,r\mapsto q,p,r }[/math]인 LFT가 존재한다. 보조 정리 2에 의해 이 LFT는 대합이다.

정리 (2대합 정리)

[math]\displaystyle{ \mathbb{RP}^1 }[/math] 위의 임의의 LFT는 두 대합의 합성함수이다.

증명 [math]\displaystyle{ h }[/math]가 임의의 LFT라 가정하자. 만약 [math]\displaystyle{ h=id }[/math]이면, [math]\displaystyle{ h=id\circ id }[/math]이고, 항등함수는 대합이므로 증명이 끝난다. 아니라면, 고정점이 아닌 점이 하나 존재한다. 이 점을 [math]\displaystyle{ p }[/math]라 하고, [math]\displaystyle{ h\left(p\right)=r }[/math]이라 하자. 그리고 [math]\displaystyle{ h\left(r\right)=q }[/math]라 가정하자. 만약 [math]\displaystyle{ p=q }[/math]이면 [math]\displaystyle{ h }[/math]는 두 점을 교환하고, 보조 정리 2에 의해 [math]\displaystyle{ h }[/math]는 대합이다. 그러면 [math]\displaystyle{ h=h\circ id }[/math]라 증명이 끝난다. 이제, [math]\displaystyle{ p\neq q }[/math]라 가정하자. 한편, [math]\displaystyle{ r\neq q }[/math]인데, 이는 [math]\displaystyle{ h^{-1} }[/math]역시 LFT이고, 따라서 일대일 대응이기 때문이다. 즉, [math]\displaystyle{ p,q,r }[/math]은 서로 다른 세 점이다. 그러면 보조 정리 3에 의해 [math]\displaystyle{ p,q }[/math]는 교환하고 [math]\displaystyle{ r }[/math]은 고정시키는 대합 [math]\displaystyle{ f }[/math]가 존재한다. 그러면, [math]\displaystyle{ f\circ h\left(p\right)=f\left(r\right)=r,f\circ h\left(r\right)=f\left(q\right)=p }[/math]이므로 [math]\displaystyle{ f\circ h }[/math]는 두 점을 교환하고, 보조 정리 2에 의해 대합이다. 한편, [math]\displaystyle{ f }[/math]는 대합이므로, [math]\displaystyle{ f^{-1}=f }[/math]이고, 따라서 [math]\displaystyle{ h=f^{-1}\circ\left(f\circ h\right)=f\circ\left(f\circ h\right) }[/math]이다. 즉, [math]\displaystyle{ h }[/math]는 두 대합의 합성함수이다.

정리 (3대칭 정리)

[math]\displaystyle{ \mathbb{H}^2 }[/math] 위의 임의의 뫼비우스 변환은 많아야 세 대칭 변환의 합성 함수이다.

증명 위 증명에서 쓰인 [math]\displaystyle{ h }[/math]를 뫼비우스 변환으로 확장시킨 뒤, 이게 많아야 세 대칭 변환의 합성 함수임을 보이겠다. 위 증명에서 쓰인 [math]\displaystyle{ f }[/math] [math]\displaystyle{ \partial\mathbb{H}^2 }[/math]위의 두 점 [math]\displaystyle{ p,q }[/math]를 교환하고 [math]\displaystyle{ r }[/math]를 고정시킨다. 이제, [math]\displaystyle{ f }[/math]를 [math]\displaystyle{ \mathbb{H}^2 }[/math]로 확장시키면, [math]\displaystyle{ f }[/math]는 [math]\displaystyle{ p,q }[/math]를 끝점으로 가지는 축지선 [math]\displaystyle{ L }[/math]을 집합 전체로서 고정시키게 된다. 그런데 [math]\displaystyle{ p,q }[/math]가 서로 교환되고, [math]\displaystyle{ L }[/math]이 연속이므로, [math]\displaystyle{ L }[/math] 위에 고정점 [math]\displaystyle{ u }[/math]가 적어도 하나 존재한다. 이제, [math]\displaystyle{ M }[/math]을 [math]\displaystyle{ u,r }[/math]을 지나는 축지선이라 가정하자. 그러면 [math]\displaystyle{ f }[/math]는 [math]\displaystyle{ M }[/math]을 집합 전체로서 고정시킨다. 그런데 등거리 사상은 각도를 보존하므로, [math]\displaystyle{ L,M }[/math]은 [math]\displaystyle{ u }[/math]에서 직교한다. 따라서, [math]\displaystyle{ f }[/math]는 점 [math]\displaystyle{ p,q,r }[/math]을 [math]\displaystyle{ M }[/math]에 대칭시키는 뫼비우스 변환이라 생각할 수 있다. 그리고 비조화비의 성질에 의해 [math]\displaystyle{ f }[/math]는 모든 점을 [math]\displaystyle{ M }[/math]을 기준으로 대칭시키는 변환이 된다. 한편, 위 증명에서 쓰인 [math]\displaystyle{ f\circ h }[/math]를 [math]\displaystyle{ g }[/math]라 부르자. [math]\displaystyle{ g }[/math]는 [math]\displaystyle{ p,r }[/math]을 교환하므로, 이 두 점을 끝점으로 가지는 [math]\displaystyle{ L' }[/math]을 고정시킨다. 또한, 같은 논리로 인해 [math]\displaystyle{ L' }[/math] 위에 고정점 [math]\displaystyle{ u' }[/math]가 존재한다. 그리고 [math]\displaystyle{ g }[/math]는 각도를 보존하므로, [math]\displaystyle{ u' }[/math]를 지나 [math]\displaystyle{ L' }[/math]에 수직인 축지선 [math]\displaystyle{ M' }[/math]을 고정시킨다. 만약 [math]\displaystyle{ g }[/math]가 [math]\displaystyle{ \partial\mathbb{H}^2 }[/math] 위의 점을 고정시키지 않는다면, [math]\displaystyle{ M' }[/math]의 양 끝점 [math]\displaystyle{ s,t }[/math]를 교환해야 한다. 이는 곧 [math]\displaystyle{ g }[/math]가 [math]\displaystyle{ L',M' }[/math]에 대해 대칭시키는 것과 동일함을 의미한다. 만약 [math]\displaystyle{ g }[/math]가 고정점을 가진다면, [math]\displaystyle{ g }[/math]는 [math]\displaystyle{ M' }[/math]에 대한 대칭 변환이다. 따라서, [math]\displaystyle{ h=f\circ g }[/math]는 많아야 세 대칭 변환의 합성 함수이다.

제대로 이해하지 못한 위키러가 많을 텐데, 걱정하지 말자. 이 부분은 원래 상당히 어렵다(...).

삼각형

사케리-르장드르 정리에 의하면, 절대 기하학의 삼각형은 세 내각의 합이 180° 이하여야만 한다. 사케리 사각형의 다른 정리에 따르면, 한 삼각형의 내각의 합이 180°이면 다른 모든 삼각형의 내각의 합도 180°이고, 내각의 합이 180° 미만이면 다른 모든 내각의 합도 180° 미만이다. 이 때, 전자의 경우가 유클리드 기하학이라는 것은 누구나 다 알고있다. 그런데 쌍곡 기하학은 유클리드 기하학과는 다른 절대 기하학이므로, 쌍곡 기하학의 삼각형의 내각의 합은 180° 미만이라는 사실을 쉽게 유추할 수 있다. 더욱이, 삼각형의 세 내각을 [math]\displaystyle{ \alpha,\beta,\gamma }[/math]라고 했을 때, 삼각형의 넓이는 [math]\displaystyle{ \pi-\left(\alpha+\beta+\gamma\right) }[/math]가 된다. 구면 기하학의 삼각형이 180° 보다 큰 내각의 합을 가졌고, 넓이가 [math]\displaystyle{ \left(\alpha+\beta+\gamma\right)-\pi }[/math]인 것과는 대조적. 우선, 이 사실을 증명하기 전에 힐베르트 평면에서 넓이를 어떻게 정의하는지 알아보자.

정의

힐베르트 평면에 존재하는 공간을 [math]\displaystyle{ R }[/math]이라 하자. 이 공간의 넓이는 [math]\displaystyle{ \underset{R}{\iint}\frac{1}{y^2}\mathrm{d}x\mathrm{d}y }[/math]로 정의한다.

상당히 특이해 보이는 정의일 수 있는데, 힐베르트 평면에서 길이를 어떻게 정의했는지 잘 생각한다면 이해가 갈 것이다. 그래도 모르겠다면, 우선 [math]\displaystyle{ \underset{R}{\iint}1\mathrm{d}x\mathrm{d}y }[/math]는 일반적인 유클리드 평면에서의 넓이이다. 그리고 힐베르트 평면에서 길이를 구할 때 허수부의 값으로 나눠주었다. 그런데 넓이는 2차원이므로, 허수부의 값을 제곱해서 나눠줘야 할 것이다. 넓이를 [math]\displaystyle{ y^2 }[/math]으로 나눠주는 이유는 바로 그 때문.

이제 삼각형의 넓이를 구할 것인데, 한 번에 바로 구하는 것이 아니라 여러 단계에 걸쳐서 조금씩 구할 것이다. 우선 이상 삼각형(Ideal Triangle)을 정의하자.

정의

이상 삼각형

삼각형의 세 꼭짓점이 [math]\displaystyle{ \partial\mathbb{H}^2=\mathbb{RP}^1 }[/math] 위에 존재하는 삼각형을 이상 삼각형이라 정의한다. 꼭짓점은 이상 꼭짓점(Ideal Vertex)이라 부른다.

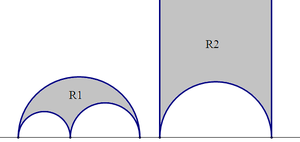
믿기진 않겠지만, 오른쪽 그림에 있는 이상하게 생긴 것들이 삼각형이다(...). R1은 세 꼭짓점이 실수인 삼각형이고, R2는 한 꼭짓점이 무한대 점인 경우. 일단 이상 삼각형의 넓이를 먼저 구해보자.

보조 정리 1

이상 삼각형의 넓이는 전부 [math]\displaystyle{ \pi }[/math]이다.

증명 임의의 이상 삼각형 R1을 생각하자. R1의 꼭짓점의 좌표가 [math]\displaystyle{ p,q,r }[/math]이라면, 적당한 뫼비우스 변환이 존재하여 [math]\displaystyle{ p,q,r\mapsto-1,1,\infty }[/math]을 할 수 있다. 변환된 삼각형을 R2라 하자. 그런데 뫼비우스 변환은 등거리 사상이라 넓이를 보존하므로, R1과 R2의 넓이는 같다. 이제 넓이를 구해보자. [math]\displaystyle{ R2=\underset{R2}{\iint}\frac{1}{y^2}\mathrm{d}x\mathrm{d}y=\int_{-1}^1\int_{\sqrt{1-x^2}}^\infty\frac{1}{y^2}\mathrm{d}y\mathrm{d}x=\int_{-1}^1\left[-\frac{1}{y}\right]_{\sqrt{1-x^2}}^\infty\mathrm{d}x=\int_{-1}^1\frac{1}{\sqrt{1-x^2}}\mathrm{d}x=\left[\arcsin x\right]_{-1}^1=\frac{\pi}{2}-\left(-\frac{\pi}{2}\right)=\pi }[/math] 따라서, 임의의 이상 삼각형의 넓이는 [math]\displaystyle{ \pi }[/math]이다.

보조 정리 2

이상 꼭짓점이 있는 삼각형

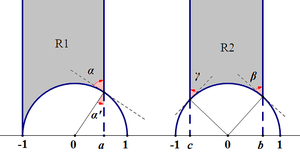
오른쪽 그림에서, R1과 R2의 넓이는 각각 [math]\displaystyle{ \pi-\alpha,\pi-\left(\alpha+\beta\right) }[/math]이다.

증명 우선 R1의 넓이부터 구하자. 이상 꼭짓점이 아닌 꼭짓점의 각도를 [math]\displaystyle{ \alpha }[/math]라고 하자. 그 꼭짓점에서 수직선을 긋고, 실수축과 만나는 점을 [math]\displaystyle{ a }[/math]라 하자. 이제, R1의 넓이를 정의를 이용하여 구하자. [math]\displaystyle{ R1=\int_{-1}^a\int_{\sqrt{1-x^2}}^\infty\frac{1}{y^2}\mathrm{d}y\mathrm{d}x=\arcsin a+\frac{\pi}{2} }[/math]. 한편, [math]\displaystyle{ \sin\alpha'=\sin\left(\frac{\pi}{2}-\alpha\right)=a }[/math]이므로, [math]\displaystyle{ \arcsin a=\frac{\pi}{2}-\alpha }[/math]이다. 따라서, [math]\displaystyle{ R1=\pi-\alpha }[/math]. 한편, 두 개의 이상 꼭짓점을 가진 삼각형은 뫼비우스 변환을 통해 R1과 비슷하게 바꿀 수 있다. 따라서, 두 개의 이상 꼭짓점을 가진 삼각형의 넓이는 [math]\displaystyle{ \pi- }[/math](한 내각) 이다. R2의 넓이는 R1과 비슷하게 구할 수 있다. 중간 계산을 생략하면, [math]\displaystyle{ R2=\arcsin a-\arcsin b=\left(\frac{pi}{2}-\alpha\right)-\left(\beta-\frac{\pi}{2}\right)=\pi-\left(\alpha+\beta\right) }[/math]이다. 마찬가지로, 한 개의 이상 꼭짓점을 가진 삼각형은 뫼비우스 변환을 통해 R2와 비슷한 모양으로 바꿀 수 있다. 따라서, 한 개의 이상 꼭짓점을 가진 삼가형의 넓이는 [math]\displaystyle{ \pi- }[/math](두 내각의 합) 이다.

정리

힐베르트 평면의 삼각형

삼각형의 세 내각을 [math]\displaystyle{ \alpha,\beta,\gamma }[/math]라고 했을 때, 삼각형의 넓이는 [math]\displaystyle{ \pi-\left(\alpha+\beta+\gamma\right) }[/math]이다.

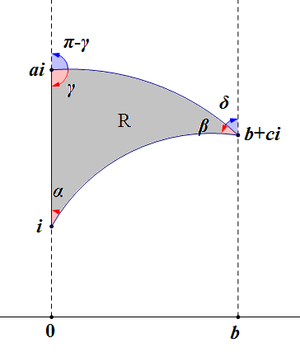
증명 뫼비우스 변환을 통해, 한 꼭짓점을 [math]\displaystyle{ i }[/math]로, 다른 한 꼭짓점을 허수축 위로([math]\displaystyle{ ai }[/math]), 마지막 꼭짓점의 실수부가 양수가 되게 옮길 수 있다([math]\displaystyle{ b\gt 0 }[/math]). 이제, R1을 [math]\displaystyle{ i,b+ci,\infty }[/math]를 꼭짓점으로 갖는 삼각형, R2를 [math]\displaystyle{ ai,b+ci,\infty }[/math]를 꼭짓점으로 갖는 삼각형이라 하자. 그러면, [math]\displaystyle{ R=R1-R2 }[/math]이다. 한편, 보조 정리 2에 의해 [math]\displaystyle{ R1=\pi-\left(\alpha+\beta+\delta\right),R2=\pi-\left(\pi-\gamma+\delta\right) }[/math]이고, 따라서 [math]\displaystyle{ R=\pi-\left(\alpha+\beta+\gamma\right) }[/math]이다.

따름 정리

힐베르트 평면에서 삼각형의 세 내각의 합은 0°보다 크고 180° 보단 작다.

증명 세 내각의 합을 [math]\displaystyle{ A }[/math]라 하자. 삼각형의 넓이는 양수이므로, [math]\displaystyle{ \pi-A\gt 0 }[/math]에서 [math]\displaystyle{ A\lt \pi }[/math]를 얻는다. 또한, 세 내각의 합은 양수이므로, [math]\displaystyle{ 0\lt A }[/math]이다. 정리하면 [math]\displaystyle{ 0\lt A\lt \pi }[/math]이다.

삼각형의 넓이를 구했다면, 이젠 삼각함수로 넘어갈 차례. 구면 기하학만의 사인 법칙과 코사인 법칙이 존재했듯이, 힐베르트 평면에서도 고유한 사인 법칙과 코사인 법칙이 존재한다. 증명은 생략하고, 결과만 알아놓자.

코사인 법칙

[math]\displaystyle{ \cos\alpha=\frac{-\cosh\left(a\right)+\cosh\left(b\right)\cdot\cosh\left(c\right)}{\sinh\left(b\right)\cdot\sinh\left(c\right)} }[/math] [math]\displaystyle{ \cos\beta=\frac{-\cosh\left(b\right)+\cosh\left(c\right)\cdot\cosh\left(a\right)}{\sinh\left(c\right)\cdot\sinh\left(a\right)} }[/math] [math]\displaystyle{ \cos\gamma=\frac{-\cosh\left(c\right)+\cosh\left(a\right)\cdot\cosh\left(b\right)}{\sinh\left(a\right)\cdot\sinh\left(b\right)} }[/math]

사인 법칙

[math]\displaystyle{ \frac{\sinh\left(a\right)}{\sin\alpha}=\frac{\sinh\left(b\right)}{\sin\beta}=\frac{\sinh\left(c\right)}{\sin\gamma} }[/math]

수학에 관심이 있는 사람이라면, [math]\displaystyle{ \cosh,\sinh,\tanh }[/math]를 쌍곡함수라 부르고, 삼각함수와 비슷한 성질을 가진다는 것을 알 것이다. 그 이유가 여기서 밝혀지는데, 쌍곡 기하학에서 쓰여서 쌍곡 함수인 것이고, 쌍곡 기하학의 삼각 함수에서 쓰이기 때문에 삼각 함수와 비슷한 성질을 가지는 것이다.

평행선

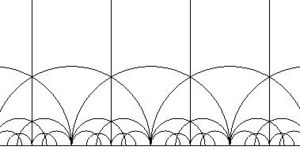
쌍곡 기하학과 다른 기하학을 구분하는 것 중 하나가 바로 평행선이다. 한 직선(측지선)과 다른 점이 주어졌을 때, 직선에 평행하면서 주어진 점을 지나는 선이 유클리드 기하학에서는 유일하고, 타원 기하학에서는 없다. 조건을 만족하는 선이 2개 이상이면 쌍곡 기하학이 되는데, 힐베르트 평면에서 직접 그려보면서 찾아보면 2개가 아니라 무한히 많다는 사실을 쉽게 알 수 있다. 참고로 두 측지선이 힐베르트 평면 내에서 교점을 가지지만 않으면 평행한 것으로 간주하므로 유클리드 기하학에서의 평행선을 생각하면 곤란하다. 하나 예를 들면, 이상 삼각형의 세 변은 전부 평행하다. 교점이 있긴 있지만, 힐베르트 평면 내부가 아닌 경계선에 존재하기 때문에 무효로 처리.

한편, [math]\displaystyle{ \partial\mathbb{H}^2 }[/math]에서 조차도 교점을 가지지 않는 두 평행선을 초평행(Ultraparallel)하다고 한다. 초평행한 두 측지선은 독특한 성질을 하나 갖는데, 바로 두 측지선에 동시에 직교하는 측지선이 유일하다는 것이다. 유클리드 기하학에서 평행한 두 직선에 동시에 수직인 직선이 무한한 것과는 대조적. 만약 두 측지선이 [math]\displaystyle{ \partial\mathbb{H}^2 }[/math]에서 교점을 가지면 두 측지선에 동시에 직교하는 측지선은 존재하지 않는다. 이제 이 사실을 증명하자.

정리 (초평행 정리)

초평행한 두 측지선에 동시에 직교하는 측지선은 유일하다. 만약 두 측지선이 초평행하지 않다면, 두 측지선에 동시에 직교하는 측지선은 존재하지 않는다.

증명 우선 두 측지선이 초평행하다고 가정하자. 그럼 두 가지 가능성이 존재한다. 한 측지선이 수직선, 다른 측지선은 반원 일반성을 잃지 않고 수직선은 허수축으로, 다른 축지선([math]\displaystyle{ L }[/math]이라 부르자)은 양 끝점이 1과 [math]\displaystyle{ p \left(p\gt 1\right) }[/math]라고 가정하자. 허수축에 수직인 측지선은 0을 중심으로 하는 반원이다([math]\displaystyle{ M }[/math]이라 부르자). 이제 [math]\displaystyle{ M }[/math]의 유클리드 반지름을 [math]\displaystyle{ R }[/math]이라 하고, [math]\displaystyle{ L }[/math]과 직교한다고 가정하자. 그러면 0, 반원 [math]\displaystyle{ L }[/math]의 중심, [math]\displaystyle{ L,M }[/math]의 교점을 세 꼭짓점으로 하는 유클리드 삼각형은 교점에서 직각을 가지는 직각삼각형이다. 그러면 피타고라스 정리에 의해, [math]\displaystyle{ R^2+\left(\frac{p-1}{2}\right)^2=\left(\frac{p}{2}\right)^2 }[/math]이고, 이를 풀면 [math]\displaystyle{ R=\frac{\sqrt{2p-1}}{2} }[/math]이다. 이 값은 유일하므로, [math]\displaystyle{ M }[/math]은 유일하다. 두 측지선 모두 반원 두 측지선의 끝점을 각각 [math]\displaystyle{ p,q }[/math]와 [math]\displaystyle{ r,s }[/math]라 부르자([math]\displaystyle{ p\lt q\lt r\lt s }[/math]). 적당한 뫼비우스 변환이 존재하여, [math]\displaystyle{ p\mapsto0,q\mapsto\infty,r\mapsto1,s\mapsto s' \left(s'\gt 1\right) }[/math]이 가능하다. 그러면 1번 케이스에 의해 증명이 끝났다. 이제 두 측지선이 초평행하지 않다고 가정하자. 그럼 세 가지 가능성이 존재한다. 두 측지선 모두 수직선 (교점이 없는 것 처럼 보이지만, 사실 [math]\displaystyle{ \infty }[/math]에서 교차한다) 일반성을 잃지 않고 한 수직선을 허수축이라 가정하자. 허수축에 수직인 측지선은 0이 중심인 반원인데, 반원과 다른 수직선은 반드시 직각보다 작은 각도로 교차한다. 따라서 두 측지선에 동시에 직교하는 측지선은 존재하지 않는다. 한 측지선이 수직선, 다른 측지선은 반원 두 측지선의 교점과 [math]\displaystyle{ \infty }[/math]를 교환하는 뫼비우스 변환을 생각해주자. 그럼 수직선은 그대로 남고(실제론 위아래가 뒤집힌 상태), 반원은 다른 수직선으로 변한다. 그러면 1번 케이스에 의해 증명이 끝났다. 두 측지선 모두 반원 두 측지선의 교점을 [math]\displaystyle{ \infty }[/math]로 보내는 뫼비우스 변환을 생각해주자. 그럼 두 측지선은 서로 다른 수직선으로 변한다. 역시 1번 케이스에 의해 증명이 끝났다.

푸앵카레 원판

푸앵카레 원판은 앙리 푸앵카레의 이름을 딴 쌍곡 기하학의 모델로써, 힐베르트 평면과 함께 쌍곡 기하학 모델에서 가장 자주 쓰인다. 참고로 밀레니엄 문제 중 하나인 푸앵카레 추측의 그 푸앵카레 맞다.

푸앵카레 원판은 힐베르트 평면에서 특정한 뫼비우스 변환 [math]\displaystyle{ M:\mathbb{C}\to\mathbb{C},M\left(z\right)=\frac{iz+1}{z+i} }[/math]을 함으로써 얻어지며, 정의역이 [math]\displaystyle{ \mathbb{H}^2 }[/math]이면 치역은 [math]\displaystyle{ \mathbb{D}=\left\{z|\left|z\right|\lt 1\right\} }[/math]이다. 우선 몇 가지 점을 대입하여 값을 확인해 보자.

[math]\displaystyle{ M\left(0\right)=-i,M\left(1\right)=1,M\left(-1\right)=-1,M\left(\infty\right)=i,M\left(i\right)=0 }[/math]

독립변수 [math]\displaystyle{ i }[/math]를 제외하고는 전부 [math]\displaystyle{ \partial\mathbb{H}^2 }[/math]의 값임에 일단 주의하자. 눈에 띄는 점은, 실사영선의 점을 대입하면 단위원 위의 점이 튀어나온다는 것이다. 실사영선이 힐베르트 평면의 경계선이고, 단위원이 푸앵카레 원판의 경계선임을 생각해보면 푸앵카레 원판은 힐베르트 평면을 동그랗게 말아 압축시킨 것이라고 할 수 있다. 그럼 힐베르트 평면 위의 점들은 정말로 전부 푸앵카레 원판 안으로 들어갈까? 이 사실을 한번 확인해보자.

정리

[math]\displaystyle{ M:\mathbb{H}^2\to\mathbb{D} }[/math]은 일대일 대응 함수이다.

증명 [math]\displaystyle{ M\left(u\right)=M\left(v\right) }[/math]이라 가정하고, 식을 정리하면 [math]\displaystyle{ u=v }[/math]를 얻는다. 따라서 [math]\displaystyle{ M }[/math]은 일대일 함수이다. 이제, 임의의 [math]\displaystyle{ w=a+bi\in\mathbb{D} }[/math]를 잡자. 행렬을 이용하면, [math]\displaystyle{ M^{-1}\left(w\right)=\frac{iw-1}{-w+i}=z }[/math]임을 쉽게 알 수 있다. 한편, [math]\displaystyle{ z }[/math]의 분모를 실수화시켜주면, [math]\displaystyle{ z=\frac{a-b-1+i\left(a^2+b^2+a-b\right)}{a^2+b^2-2a+1} }[/math]이고, [math]\displaystyle{ \Im\left(z\right)=\frac{a^2+b^2+a-b}{\left(a-1\right)^2+b^2}\gt 0 }[/math]이다. 이는 곧 [math]\displaystyle{ z\in\mathbb{H}^2 }[/math]임을 의미한다. 이제, [math]\displaystyle{ \left|M\left(z\right)\right|^2=\frac{\left|iz+1\right|^2}{\left|z+i\right|^2}=\frac{\left|i\right|\left|z-i\right|^2}{\left|z+i\right|^2}\leq1 }[/math]가 참임을 보여야 하는데, 잘 정리해주면 [math]\displaystyle{ y=\Im\left(z\right)\geq0,\,\,\,\left(z=x+yi\right) }[/math]가 나오고, 이는 참인 명제이므로 [math]\displaystyle{ \left|M\left(z\right)\right|\leq1 }[/math]를 얻는다. 만약 [math]\displaystyle{ \left|M\left(z\right)\right|=1 }[/math]이면 [math]\displaystyle{ y=0 }[/math]인데, 이 경우에는 [math]\displaystyle{ z\in\partial\mathbb{H}^2 }[/math]이므로 경계선은 경계선으로, 내부의 점은 내부의 점으로 변환됨을 확인할 수 있다. 따라서, [math]\displaystyle{ M }[/math]는 전사 함수이다.

힐베르트 평면에서 푸앵카레 원판으로 변환시키는 뫼비우스 변환 [math]\displaystyle{ M }[/math]이 일대일 대응임을 알았으므로, 푸앵카레 원판의 모든 것은 [math]\displaystyle{ M^{-1} }[/math]을 통해 힐베르트 평면에서 조사할 수 있다. 그렇기 때문에 푸앵카레 원판에 대해 더 분석하는 것은 큰 의미가 없으니, 몇 가지 중요한 점만 짚자.

1. 경로의 길이

   [math]\displaystyle{ \int_0^1\frac{2\left|\gamma'\left(t\right)\right|}{1-\left|\gamma\left(t\right)\right|^2}\mathrm{d}t }[/math]로 정의된다. 아니면 [math]\displaystyle{ M^{-1} }[/math]을 이용해 힐베르트 평면으로 바꾼 뒤, 힐베르트 평면에서 길이를 구하자.

2. 측지선

   힐베르트 평면의 측지선은 양끝점이 실사영선 위에 존재한다. 실사영선은 단위원으로 변환되므로, 푸앵카레 원판의 측지선은 단위원 위에 끝점이 존재하게 된다. 허수축은 [math]\displaystyle{ -i }[/math]와 [math]\displaystyle{ i }[/math]를 잇는 수직선으로 변환되며, 나머지 측지선들은 단위원에 직교하는 호로 변환된다.

3. 등거리 사상

   힐베르트 평면과 비슷하게, 쌍곡, 포물선, 타원 변환이 존재한다. 세 변호나 전부 힐베르트 평면과 크게 다르지 않으므로 자세한 설명은 생략. 한편, 힐베르트 평면의 타원 변환은 [math]\displaystyle{ f\leftrightarrow\begin{bmatrix}\cos\theta&&-\sin\theta\\\sin\theta&&\cos\theta\end{bmatrix} }[/math]와 닮았는데, [math]\displaystyle{ M\circ f\circ M^{-1} }[/math]([math]\displaystyle{ M }[/math]에 관한 켤레)를 계산해주면, [math]\displaystyle{ \begin{bmatrix}-2\cos\theta+2\sin\theta&&0\\0&&-2\cos\theta-2\sin\theta\end{bmatrix}\leftrightarrow\frac{-2e^{-i\theta}z}{-2e^{i\theta}}=e^{-2i\theta}z }[/math]가 나온다. 최종 결과값은 복소 평면에서 원점을 기준으로 [math]\displaystyle{ -2\theta }[/math]만큼 회전시키는 변환인데, 힐베르트 평면의 타원 변환의 회전 각도가 [math]\displaystyle{ \theta }[/math]가 아닌 [math]\displaystyle{ -2\theta }[/math]인 이유는 바로 이 때문.

같이 보기

• 결합 기하학
• 절대 기하학
• 유클리드 기하학
• 타원 기하학