정의[편집 | 원본 편집]
영어로는 Arc. 원주의 일부분을 말한다. 현이나 원주각과는 달리 그리 많은 성질이 존재하지 않는 불쌍한 존재.
성질[편집 | 원본 편집]
1. 한 원, 혹은 합동인 두 원에서 중심각의 크기가 같은 호는 길이가 같다. 역으로 길이가 같은 호는 중심각도 같다.
2. 호의 길이와 현의 길이는 비례하지 않는다.
3. 반지름을 [math]\displaystyle{ r }[/math], 중심각을 [math]\displaystyle{ \theta }[/math]라 했을 때, 호의 길이는 [math]\displaystyle{ r\theta }[/math]이다.
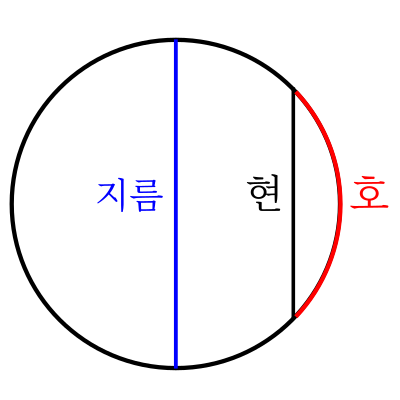
|
| 원의 지름은 가장 긴 현과 호를 갖는다. |
증명[편집 | 원본 편집]
1, 2. 현 (수학) 항목을 참조.
3. 호의 길이를 [math]\displaystyle{ l }[/math]이라 하자. 그럼, 원주와의 비례식에서 [math]\displaystyle{ 2\pi r:2\pi=l:\theta }[/math]이고, [math]\displaystyle{ l }[/math]에 관해 풀어주면 [math]\displaystyle{ l=r\theta }[/math]이다.
부채꼴[편집 | 원본 편집]
영어로는 Sector. 두 반지름과 그 사이의 호로 이루어진 도형을 말한다. 케이크 조각과 비슷한 모양. 호는 성질이라도 있지 얘는 공식밖에 없다. 안습 넓이는 [math]\displaystyle{ \frac{1}{2}r^2\theta }[/math]이며, 증명은 호의 길이를 구하는 방법과 비슷하게 원의 넓이와 비례식을 세운다. 호의 길이가 [math]\displaystyle{ r\theta }[/math]임을 이용하여 [math]\displaystyle{ \frac{1}{2}rl }[/math]이라 해도 된다. 둘레는 [math]\displaystyle{ l+2r }[/math]. 부채꼴은 정말로 이게 끝이다.