정의[편집 | 원본 편집]
호의 양 끝점과 원주 위의 다른 한 점을 이었을 때 생기는 두 현사이의 각을 그 호에 대한 원주각(Inscribed Angle)이라 부른다. 그리고 같은 호의 양 끝점과 원의 중심을 이었을 때 생기는 각을 중심각(Central Angle)이라 부른다.
성질[편집 | 원본 편집]
- 원주각의 크기는 중심각의 크기의 절반.
- 한 호에 대한 원주각의 크기는 모두 같다.
- 한 원, 혹은 합동인 두 원에서 호의 길이가 같으면 원주각의 크기도 같다. 역으로 원주각의 크기가 같으면 호의 길이도 같다.
- 원주각은 원 내부의 점을 이은 각보다는 작고, 원 외부의 점을 이은 각보다는 크다. 단, 두 점 모두 호를 기준으로 같은 쪽에 있어야 한다.
증명[편집 | 원본 편집]
1번 성질을 증명하면 2번 성질도 같이 증명된다. 1번 성질을 증명하기 위해선 세 가지 경우를 모두 살펴봐야 한다.
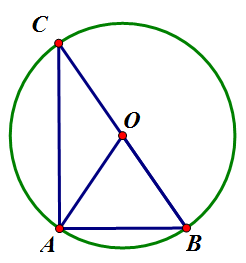
i. 한 현이 지름인 경우: [math]\displaystyle{ \overline{OA}=\overline{OB}=\overline{OC} }[/math]이므로 [math]\displaystyle{ \angle{OCA}=\angle{OAC} }[/math]. 외각은 두 내각의 합이므로 [math]\displaystyle{ \triangle{OCA} }[/math]에서 [math]\displaystyle{ \angle{AOB}=2\angle{ACB} }[/math].
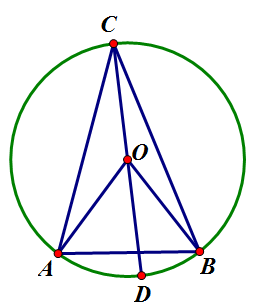
ii. 두 현이 반지름과 겹치지 않는 경우: i에서 증명한 사실을 활용하면, [math]\displaystyle{ \angle{AOD}=2\angle{ACD} }[/math]이고 [math]\displaystyle{ \angle{BOD}=2\angle{BCD} }[/math]이다. 따라서, [math]\displaystyle{ \angle{AOB}=\angle{AOD}+\angle{BOD}=2\angle{ACD}+2\angle{BCD}=2\angle{ACB} }[/math]이다.
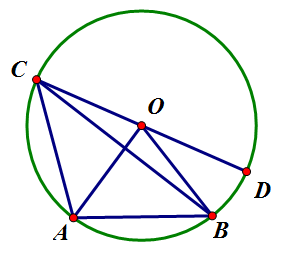
iii. 한 현이 반지름과 겹치는 경우: i에서, [math]\displaystyle{ \angle{DOA}=2\angle{DCA} }[/math]. 마찬가지로 i에서, [math]\displaystyle{ \angle{DOB}=2\angle{DCB} }[/math]. 따라서, [math]\displaystyle{ \angle{AOB}=\angle{AOD}-\angle{BOD}=2\angle{DCA}-2\angle{DOB}=2\angle{ACB} }[/math].
따라서 중심각은 원주각의 2배이다.
3. 호의 길이가 같으면 중심각의 크기가 같다. 1번 성질에서 중심각의 크기가 같으면 원주각의 크기가 같음을 알 수 있다. 역으로 원주각의 크기가 같으면 중심각의 크기가 같고, 중심각의 크기가 같으면 호의 길이가 같다. 자세한 것은 호 (수학) 참고.
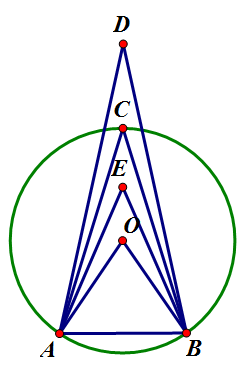
4. 한 호에 대한 원주각의 크기는 모두 같기 때문에, 세 점과 원의 중심이 공선점일 때만 증명하면 된다. [math]\displaystyle{ \angle{AEO}=\angle{ACE}+\angle{CAE} }[/math]라서 [math]\displaystyle{ \angle{AEO}\gt \angle{ACO} }[/math]이고, 같은 방법으로 [math]\displaystyle{ \angle{ACO}\gt \angle{ADO} }[/math]이다. 반대쪽에서도 같은 방법으로 [math]\displaystyle{ \angle{BEO}\gt \angle{BCO}\gt \angle{BDO} }[/math]가 성립한다. 따라서 [math]\displaystyle{ \angle{AEB}\gt \angle{ACB}\gt \angle{ADB} }[/math]가 성립한다.