원 (도형)

원(圓, 영어: circle)은 "유클리드 평면 상의 한 점에서 거리가 일정한 점들의 집합"을 의미한다.

해석기하학을 도입하면 [math]\displaystyle{ x^2+y^2+Ax+By+C=0 }[/math]으로 나타내며, 이는 이차곡선의 일종이다. 이차곡선의 일반식에 대입하면 [math]\displaystyle{ ax^2+by^2+cxy+dx+ey+f=0 }[/math]에서 [math]\displaystyle{ a=b \neq 0 }[/math]이며, [math]\displaystyle{ c=0 }[/math]인 경우가 원이 된다. 타원의 일종으로 보기도 하는데, 이심률이 0인 타원이 바로 원이 되기 때문이다. (또는 두 초점이 일치하는 경우)

용어[편집 | 원본 편집]

중심: 말 그대로 원의 중심. 원주 위의 임의의 점과 거리를 제어도 거리가 같은 한 점을 말한다.
원주: 원의 둘레.
원주율: 원주와 지름의 비. 이 값은 항상 일정한데, 자세한 것은 항목 참조.
반지름: 원의 중심과 원주 위의 임의의 한 점 사이의 거리.
할선: 어떤 직선이 원과 두 점에서 만날 때, 그 직선을 할선이라 한다.
현: 할선의 부분집합으로, 원에 포함되는 부분을 (원주 위의 두 점 포함) 현이라 한다.
접선: 어떤 직선이 원과 한 점에서 만날 때, 그 직선을 접선이라 한다. 할선의 특별한 경우라 생각할 수 있다.
접점: 접선과 원이 만나는 점.
호: 원주의 일부분. 즉, 부분집합.
부채꼴: 원의 부분집합으로, 호의 양 끝점과 원의 중심을 이은 두 선분과 호를 이은 도형을 말한다.
중심각: 부채꼴에서 호의 양 끝점과 원의 중심을 이은 두 선분의 사이각을 말한다.
원주각: 어떤 호의 양 끝점과 호 위에 있지않은 원주 위의 다른 한 점을 이었을 때 생기는 두 현의 사이각을 그 호에 대한 원주각이라 말한다.
접현각: 접선과 접점을 포함하는 현 사이의 각.

종류[편집 | 원본 편집]

실원 : 실수평면위에 존재하는 원
점 : 평면 위의 한 점
허원 : 실수평면 위에 존재하지 않는 원

두 원의 위치관계[편집 | 원본 편집]

원 [math]\displaystyle{ A }[/math]의 반지름을 [math]\displaystyle{ r_A }[/math], 원 [math]\displaystyle{ B }[/math]의 반지름을 [math]\displaystyle{ r_B }[/math]라 하고, 두 원의 중심의 거리를 [math]\displaystyle{ d }[/math]라고 하자.

두 원이 너무 멀리 떨어져 있어서 만나지 않는 경우: [math]\displaystyle{ r_A+r_B \lt d }[/math]
두 원이 외접하는 경우: [math]\displaystyle{ d = r_A+r_B }[/math]
두 원이 두 점에서 만나는 경우: [math]\displaystyle{ |r_A-r_B| \lt d \lt r_A+r_B }[/math]
두 원이 내접하는 경우: [math]\displaystyle{ 0 \lt d = |r_A-r_B| }[/math]
한 원이 다른 원 내부에 있는 경우: [math]\displaystyle{ 0 \lt d \lt |r_A-r_B| }[/math]
두 원이 중심을 공유하는 경우(동심원): [math]\displaystyle{ d = 0 }[/math]
- 특별히 [math]\displaystyle{ d = 0 }[/math]이면서 [math]\displaystyle{ r_A = r_B }[/math]이기까지 하면 두 원이 ‘일치’하는 경우가 된다.

성질[편집 | 원본 편집]

이와 관련한 내용은 호 (수학), 현 (수학), 원주각에서 볼 수 있습니다.

원의 반지름을 [math]\displaystyle{ r }[/math]이라 했을 때, 원주의 길이는 [math]\displaystyle{ 2\pi r }[/math], 원의 넓이는 [math]\displaystyle{ \pi r^2 }[/math]이다.
모든 원은 서로 닮음이다.
평면 위에 공선점이 아닌 임의의 세 점을 고르면, 그 세 점을 모두 지나는 원이 유일하게 존재한다.
원의 중심에서 접선에 내린 직선은 접선과 직교한다.
현으로 인해 생기는 두 호 중 짧은 쪽의 호에 대한 원주각와 접현각의 크기는 같다.
원 밖의 한 점에서 원에 그은 두 접선의 길이는 같다.

증명[편집 | 원본 편집]

미적분을 사용하면 된다.
외심 참조.
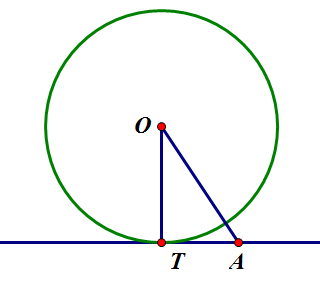
귀류법을 사용한다. 만약 [math]\displaystyle{ \overline{OT}\perp\overleftrightarrow{T} }[/math]가 아니라면 [math]\displaystyle{ \overline{OA}\perp\overline{TA} }[/math]를 만족시키는 점 [math]\displaystyle{ A }[/math]가 접선 [math]\displaystyle{ T }[/math]위에 존재한다. 따라서 원의 중심과 접선 사이의 거리는 [math]\displaystyle{ \overline{OA} }[/math]이다. 그런데 직각삼각형 [math]\displaystyle{ OAT }[/math]에서 빗변 [math]\displaystyle{ \overline{OT} }[/math]가 [math]\displaystyle{ \overline{OA} }[/math]가 더 길어야 하므로^[1] 반지름이 원의 중심과 접선 사이의 거리보다 길다는 게 되고, 이는 접선이 실은 할선이었다는 결론이 나와 모순이다. 따라서 반지름과 접선은 직교한다.
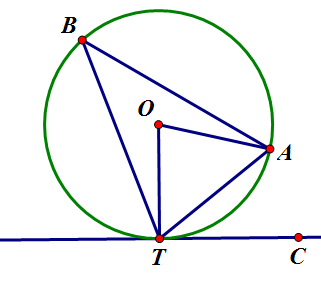
[math]\displaystyle{ \angle{OTA}=\alpha }[/math]라 하자. 그럼 [math]\displaystyle{ \overline{OT}=\overline{OA} }[/math]이므로 (반지름) [math]\displaystyle{ \triangle{OTA} }[/math]는 이등변삼각형이고, 따라서 [math]\displaystyle{ \angle{OAT}=\alpha }[/math]이다. 곧, [math]\displaystyle{ \angle{TOA}=180^{\circ}-2\alpha }[/math]이다. 한편, [math]\displaystyle{ \overline{OT} }[/math]와 접선 [math]\displaystyle{ TC }[/math]가 직교하므로 [math]\displaystyle{ \angle{OTC}=90^{\circ} }[/math]. 따라서 [math]\displaystyle{ \angle{ATC}=90^{\circ}-\alpha=\frac{1}{2}\angle{TOA} }[/math]이다. 이제 원의 성질 2번에 의해 증명하고자 하는 바가 증명되었다.
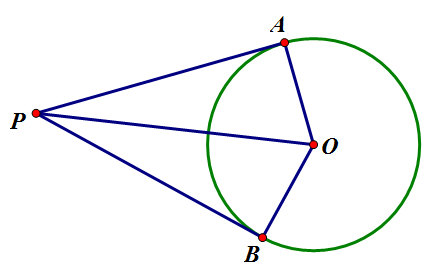
[math]\displaystyle{ \angle{OAP}=\angle{OBP}=\angle{R} }[/math] (4번 성질), [math]\displaystyle{ \overline{OA}=\overline{OB} }[/math] (반지름), [math]\displaystyle{ \overline{PO} }[/math]공통. [math]\displaystyle{ \therefore\triangle{OAP}\cong\triangle{OBP} }[/math] (RHS 합동). [math]\displaystyle{ \therefore\overline{PA}=\overline{PB} }[/math].

원의 상징 및 사용[편집 | 원본 편집]

대체로 원은 완전함을 상징하는 경우가 많다.
원불교의 상징으로 이 원을 사용한다.
우주에서 가장 아름다운 도형으로 여겨진다.
동양에서 별은 ☆ 모양이 아니라 둥근 원으로 표현된다. ○

각주

↑ 사인 법칙 참조

[1] 사인 법칙 참조

[1]