외심

Circumcenter

정의

다각형의 외접원이 존재할 때, 그 외접원의 중심을 외심이라 부른다. 하지만 보통 외심이라고 하면 삼각형의 외심을 말한다. 어떤 다각형의 외심, 즉 외접원이 존재하기 위한 조건은 모든 꼭짓점까지의 거리가 동일한 점이 존재하면 된다. 만약 그런 점이 존재할 경우, 그 점이 외심이 되며, 외심으로부터 한 꼭짓점까지의 거리가 외접원의 반지름이 된다. 참고로 이 조건은 모든 변의 수직이등분선이 한 점에서 만난다는 사실과 동치이다.

삼각형의 경우에는 반드시 외심이 존재하며, 사각형 부터는 외접원이 존재할 수도 있고 하지 않을 수도 있다. 이 문서에서는 삼각형의 외심에 대해 다루며, 다른 외접원에 관해서는 공원점 항목을 참조하자.

외심만의 성질

1. 삼각형의 세 변의 수직이등분선은 반드시 한 점에서 만난다.
2. 외심은 예각삼각형의 경우 삼각형의 안쪽에, 직각삼각형은 빗변 위에, 둔각삼각형의 경우 삼각형 밖에 존재한다.
3. 외접원의 반지름의 길이를 [math]\displaystyle{ R }[/math]이라 하면, 삼각형의 넓이는 [math]\displaystyle{ 2R^2\sin A\sin B\sin C }[/math]이다.
4. 삼각형의 넓이는 [math]\displaystyle{ \frac{abc}{4R} }[/math]이다.

증명

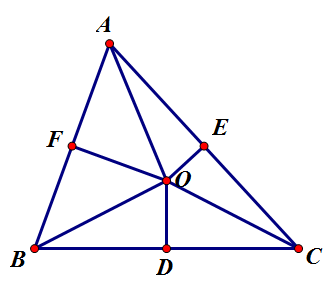
1. [math]\displaystyle{ \overline{BC},\,\overline{CA} }[/math]의 중점을 각각 [math]\displaystyle{ D, E }[/math]라 하자. 또한, [math]\displaystyle{ \overline{BC},\,\overline{CA} }[/math]의 수직이등분선의 교점을 [math]\displaystyle{ O }[/math]라 하자. 그럼 [math]\displaystyle{ \triangle{OBD}\cong\triangle{OCD},\,\triangle{OCE}\cong\triangle{OAE} }[/math](SAS 합동)이므로 [math]\displaystyle{ \overline{OB}=\overline{OC}=\overline{OA} }[/math]이다. 이제 [math]\displaystyle{ O }[/math]에서 [math]\displaystyle{ \overline{AB} }[/math]에 내린 수선의 발을 [math]\displaystyle{ F }[/math]라 하자. 그럼 [math]\displaystyle{ \triangle{OBF}\cong\triangle{OAF} }[/math](RHS 합동)이므로 [math]\displaystyle{ \overline{AF}=\overline{BF} }[/math]이다. 반대로 [math]\displaystyle{ O }[/math]에서 [math]\displaystyle{ \overline{AB} }[/math]에 내린 중선의 발을 [math]\displaystyle{ F }[/math]라 하자. [math]\displaystyle{ \triangle{OBF}\cong\triangle{OAF} }[/math](SSS 합동)이므로 [math]\displaystyle{ \angle{OFB}=\angle{OFA}=\angle{R} }[/math]이다. 따라서 세 변의 수직이등분선은 한점에서 만난다. 직각삼각형의 경우는 항목 참조, 그리고 둔각삼각형의 경우에도 같은 방법으로 증명이 가능하다.

3. 삼각형의 넓이는 [math]\displaystyle{ \frac{1}{2}bc\sin A }[/math]이고, 사인 법칙에 의해 [math]\displaystyle{ b=2R\sin B,\,c=2R\sin C }[/math]이다. 따라서 [math]\displaystyle{ S_{\triangle{ABC}}=\frac{1}{2}2R\sin B\cdot2R\sin C\sin A=2R^2\sin A\sin B\sin C }[/math].

4. 3번 성질에서 [math]\displaystyle{ S_{\triangle{ABC}}=2R^2\sin A\sin B\sin C }[/math]이다. 여기서 사인 법칙에 의해 [math]\displaystyle{ \sin A=\frac{a}{2R},\,\sin B=\frac{b}{2R},\,\sin C=\frac{c}{2R} }[/math]이므로, 이를 대입하면 [math]\displaystyle{ S_{\triangle{ABC}}=\frac{abc}{4R} }[/math].

기타 성질

• 기하학에서의 오일러의 정리에 따르면, 외심과 내심 사이의 거리는 [math]\displaystyle{ \sqrt{R\left(R-2r\right)} }[/math]이다 ([math]\displaystyle{ r }[/math]은 내접원의 반지름). 여기서 알 수 있는 사실은 외접원의 반지름의 길이는 최소한 내접원의 반지름의 길이의 두 배라는 사실이다. 등호는 외심과 내심이 일치할 때 성립한다.
• 외심, 수심, 무게중심, 구점원의 중심은 동일선상에 있다. 자세한 것은 오일러 직선 참고.

관련 항목

• 삼각형
• 공원점
• 내심
• 무게중심
• 수심 (수학)
• 방심