Euler Line
개요[편집 | 원본 편집]
오일러 직선이란, 삼각형의 여러 가지 중심을 지나는 직선을 말한다. 외심, 무게중심, 수심, 구점원의 중심, 이렇게 네 개의 점을 지나며, exeter point도 지나긴 하나 애초에 exeter point를 아는 사람이 거의 없기 때문에 이 점은 보통 생략한다. 참고로 exeter point의 정의는 아래와 같다.
“ 삼각형의 세 중선이 외접원과 만나는 점을 각각 [math]\displaystyle{ A',B',C' }[/math]이라고 하자. 또한, 점 [math]\displaystyle{ A,B,C }[/math]를 지나고, 외접원에 접하는 직선으로 만들어진 삼각형을 [math]\displaystyle{ \triangle{DEF} }[/math]라 하자. 여기서 [math]\displaystyle{ D,E,F }[/math]는 [math]\displaystyle{ A,B,C }[/math]의 맞은 편에 각각 존재한다. 그럼 [math]\displaystyle{ \overleftrightarrow{DA'},\overleftrightarrow{EB'},\overleftrightarrow{FC'} }[/math]는 한 점에서 만나는데, 이 점을 exeter point라 한다. “
정의를 보면 왜 exeter point는 빼놓고 설명하는지 이해가 될 것이다. 이해가 안되거든.
한편, 오일러 직선은 앞서 말한 5개의 중심을 지나는 한 직선이다. 즉, 저 중심들이 삼각형에 관계없이 모두 공선점이라는 소리. 단, 정삼각형만은 예외로, 정삼각형은 저 중심들이 전부 동일하기 때문이다.
증명[편집 | 원본 편집]
먼저 각 점에서 내린 수선의 발을 [math]\displaystyle{ D,E,F }[/math], 각 변의 중점을 [math]\displaystyle{ L,M,N }[/math], 그리고 각 꼭짓점에서 수심을 이은 선분의 중점을 [math]\displaystyle{ P,Q,R }[/math]이라고 하자.
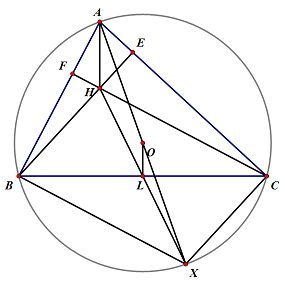
1. 세르보어의 정리: [math]\displaystyle{ \triangle{ABC} }[/math]의 수심을 [math]\displaystyle{ H }[/math], 외심을 [math]\displaystyle{ O }[/math]라 하면 [math]\displaystyle{ \overline{AH}=2\overline{OL} }[/math]이 성립한다 (아래 그림 참조).
[math]\displaystyle{ \overline{AO} }[/math]의 연장선이 외접원과 만나는 점을 [math]\displaystyle{ X }[/math]라 하자. 그럼 [math]\displaystyle{ \overline{AH}\parallel\overline{OL} }[/math]이고 (전자는 수선, 후자는 수직이등분선), [math]\displaystyle{ O }[/math]는 [math]\displaystyle{ \overline{AX} }[/math]의 중점이므로 중점연결정리의 역에 의해 [math]\displaystyle{ \overline{AH}=2\overline{OL} }[/math]이 성립한다.
2. 외심, 수심, 무게중심
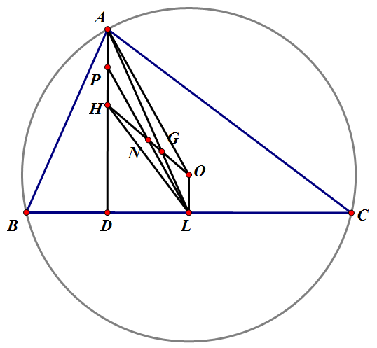
이제 [math]\displaystyle{ \overline{OH} }[/math]와 [math]\displaystyle{ \overline{AL} }[/math]의 교점을 [math]\displaystyle{ G }[/math]라고 하자. [math]\displaystyle{ \angle{AGH}=\angle{LGO} }[/math](맞꼭지각)이고, [math]\displaystyle{ \angle{GHA}=\angle{GOL} }[/math](엇각)이므로 [math]\displaystyle{ \triangle{AGH}\sim\triangle{LGO} }[/math]이다. 닮음비는 [math]\displaystyle{ \overline{AH}:\overline{LO}=2:1 }[/math]이므로, [math]\displaystyle{ \overline{AG}:\overline{GL}=2:1 }[/math]이다. 즉, [math]\displaystyle{ G }[/math]는 중선 [math]\displaystyle{ \overline{AL} }[/math]을 2:1로 내분하므로 무게중심이다. 따라서 외심, 수심, 무게중심은 공선점이다.
3. 수심, 외심, 구점원의 중심
세르보어의 정리에서 [math]\displaystyle{ \overline{PH}=\overline{OL} }[/math]이고, [math]\displaystyle{ \overline{PH}\parallel\overline{OL} }[/math]이므로 사각형 [math]\displaystyle{ PHLO }[/math]는 평행사변형이다. 평행사변형의 두 대각선의 교점을 [math]\displaystyle{ N }[/math]이라 하면, 두 대각선은 서로를 이등분하므로 [math]\displaystyle{ \overline{PN}=\overline{LN} }[/math]이다. 한편, [math]\displaystyle{ \overline{PL} }[/math]은 구점원의 지름이므로, [math]\displaystyle{ N }[/math]은 구점원의 중심이 된다. 따라서 수심, 외심, 구점원의 중심은 한 직선 위에 있다.
1, 2, 3에 의해 외심, 수심, 무게중심, 구점원의 중심은 공선점이다.