Nine-point Circle
개요[편집 | 원본 편집]
구점원이란, 삼각형의 아홉가지 점을 지나는 원을 말한다. 여기서 아홉가지 점이란, 각 변의 중점, 각 꼭짓점에서 그 대변의 수선의 발, 각 꼭짓점과 수심 사이의 중점, 이렇게 9개 점을 말한다. 평면기하학의 신비 중 하나로, 그 어떤 삼각형이라도 저 많은 점들이 다 한 원 위에 존재한다. 구점원을 부르는 다른 이름으로는 포이어바흐 원 (포이어바흐 정리에서 따옴), 오일러 원(오일러 직선에서 따옴) 이라고도 부른다.
증명[편집 | 원본 편집]
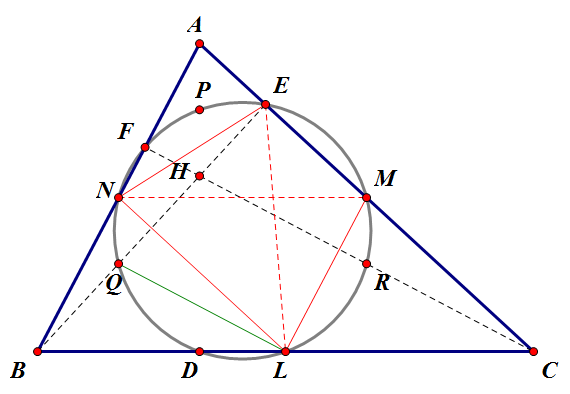
점 [math]\displaystyle{ A,B,C }[/math]에서 각 대변에 내린 수선의 발을 [math]\displaystyle{ D,E,F }[/math]라 하고, 세 수선의 교점을 [math]\displaystyle{ H }[/math]라 하자. 그리고 변 [math]\displaystyle{ \overline{BC},\,\overline{CA},\,\overline{AB} }[/math]의 중점을 각각 [math]\displaystyle{ L,M,N }[/math]이라 하자. 마지막으로, [math]\displaystyle{ \overline{AH},\,\overline{BH},\,\overline{CH} }[/math]의 중점을 각각 [math]\displaystyle{ P,Q,R }[/math]이라고 하자.
먼저 사각형 [math]\displaystyle{ ENLM }[/math]을 살펴보자 (빨간색 실선). 중점연결정리에 의해 [math]\displaystyle{ \overline{NL}\parallel\overline{AC} }[/math]이므로 사각형 [math]\displaystyle{ ENLM }[/math]은 사다리꼴이다. 이제 두 대각선을 보자 (빨간색 점선). 다시 한번 중점연결정리에 의해 [math]\displaystyle{ \overline{NM}=\frac{1}{2}\overline{BC} }[/math]이다. 한편, [math]\displaystyle{ \triangle{BEC} }[/math]는 직각삼각형이므로 빗변의 중점 [math]\displaystyle{ L }[/math]은 외심이 되며, 따라서 [math]\displaystyle{ \overline{BL}=\overline{EL}=\frac{1}{2}\overline{BC} }[/math]이다. 즉, [math]\displaystyle{ \overline{NM}=\overline{EL} }[/math]이므로, 사다리꼴 [math]\displaystyle{ ENLM }[/math]은 등변사다리꼴이다. 등변사다리꼴은 반드시 원에 내접하므로, 점 [math]\displaystyle{ E,N,L,M }[/math]은 공원점이다. 같은 방법으로 사각형 [math]\displaystyle{ FNLM, DLMN }[/math]이 등변사다리꼴임을 보일 수 있고, 이 세 사다리꼴은 모두 [math]\displaystyle{ L,M,N }[/math]을 포함하므로 한 원 위에 있다. 따라서 점 [math]\displaystyle{ D,E,F,L,M,N }[/math]은 공원점이다.
이제 삼각형 [math]\displaystyle{ \triangle{BHC} }[/math]에서, 중점연결정리에 의해 [math]\displaystyle{ \overline{QL}\parallel\overline{HC} }[/math]이고, 따라서 [math]\displaystyle{ \overline{QL}\parallel\overline{FC} }[/math]이다. 또한, 다시 한번 중점연결정리에 의해 [math]\displaystyle{ \overline{ML}\parallel\overline{AB} }[/math]임을 알 수 있다. 이 두 사실에서, [math]\displaystyle{ \angle{QLB}=\angle{FCB},\,\angle{MLC}=\angle{ABC} }[/math](동위각)이다. 한편, [math]\displaystyle{ \triangle{FBC} }[/math]에서 [math]\displaystyle{ \angle{F} }[/math]가 직각이므로, [math]\displaystyle{ \angle{FBC}+\angle{FCB}=90^\circ }[/math]이다. 따라서 [math]\displaystyle{ \angle{QLB}+\angle{MLC}=90^\circ }[/math]이고, 곧 [math]\displaystyle{ \angle{QLM}=90^\circ }[/math]이다. 그런데 [math]\displaystyle{ E }[/math]는 꼭짓점 [math]\displaystyle{ B }[/math]에서 내린 수선의 발이므로, [math]\displaystyle{ \angle{QEM}=90^\circ }[/math]. 따라서 사각형 [math]\displaystyle{ EQLM }[/math]은 두 대각의 합이 [math]\displaystyle{ 180^\circ }[/math]이고, 원에 내접한다. 특히, [math]\displaystyle{ \overline{QM} }[/math]이 그 원의 지름이다. 같은 방법으로 사각형 [math]\displaystyle{ FNLR,PDLM }[/math]이 공원점임을 보일 수 있다. 또한, 이 세 사각형은 모두 점[math]\displaystyle{ D,E,F,L,M,N }[/math] 중 세 점을 포함하므로, 같은 원 위에 있다. 따라서 점 [math]\displaystyle{ D,E,F,L,M,N,P,Q,R }[/math]은 한 원 위에 있다.
성질[편집 | 원본 편집]
1. [math]\displaystyle{ \overline{PL}=\overline{QM}=\overline{RN} }[/math]이다. 세 선분 모두 구점원의 지름이므로 성립한다.
2. 세르보어의 정리: 외심을 [math]\displaystyle{ O }[/math]라 했을 때, [math]\displaystyle{ \overline{AH}=2\overline{OL} }[/math]이다. 증명은 오일러 직선 항목을 참조.
3. 오일러 직선: 삼각형의 수심, 외심, 무게중심, 구원점의 중심은 공선점이다. 증명은 항목 참조.
4. 포이어바흐 정리: 구점원은 삼각형의 내접원과 세 방접원에 모두 접한다.
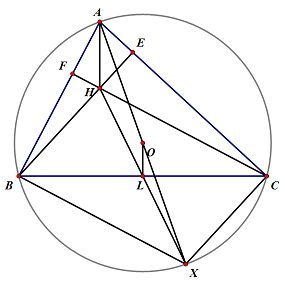
5. 구점원의 지름은 외접원의 지름의 절반이다. [math]\displaystyle{ \triangle{AHX} }[/math]에서 중점연결정리에 의해 [math]\displaystyle{ \overline{PL}=\frac{1}{2}\overline{AX} }[/math]이기 때문.
6. 구점원의 중심은 [math]\displaystyle{ \overline{OH} }[/math]의 중점이다. 세르보어의 정리에서 [math]\displaystyle{ \overline{PH}=\overline{OL} }[/math]을 유도 가능하고, 따라서 [math]\displaystyle{ PHLO }[/math]는 평행사변형이다. 평행사변형의 두 중점은 서로를 이등분하고, 더욱이 [math]\displaystyle{ \overline{PL} }[/math]이 구점원의 지름이므로, [math]\displaystyle{ \overline{OH} }[/math]의 중점은 구점원의 중심.