Centroid, Geometric Center
정의[편집 | 원본 편집]
이름 그대로 물체의 무게의 중심점. 만약 중력가속도가 동일하다면 무게중심과 질량중심은 동일하며, 중력가속도가 균일하지 않다면 질량중심과 무게중심이 다를 수도 있다. 하지만 일상생활에서는 무게중심과 질량중심을 특별히 구분할 이유는 없다. 학교에서는 삼각형의 무게중심에 대해 배우며, 삼각형의 무게중심의 정의는 세 중선의 교점이다. 세 중선의 교점이 왜 삼각형의 무게중심이 되는지에 대해서는 무게중심의 성질을 참조.
삼각형의 무게중심의 성질[편집 | 원본 편집]
- 삼각형의 세 중선은 반드시 한 점에서 만난다.
- 세 중선은 무게중심에 의해 2:1로 나눠진다.
- 세 중선에 의해 생기는 6개의 삼각형은 넓이가 같다.
- 무게중심의 벡터는 [math]\displaystyle{ \frac{\vec{a}+\vec{b}+\vec{c}}{3} }[/math]이다.
- 무게중심을 [math]\displaystyle{ G }[/math]라 하면, [math]\displaystyle{ \overline{AB}^2+\overline{BC}^2+\overline{CA}^2=3\left(\overline{GA}^2+\overline{GB}^2+\overline{GC}^2\right) }[/math]
- 무게중심, 수심, 외심, 구점원의 중심은 공선점이다.
증명[편집 | 원본 편집]
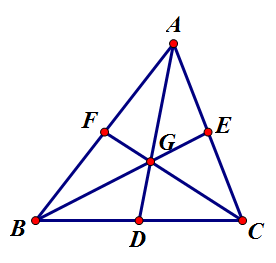
1. [math]\displaystyle{ A }[/math]와 [math]\displaystyle{ B }[/math]에서 각 대변에 내린 중선의 발을 [math]\displaystyle{ D,\,E }[/math]라 하자. 또한, 그 두 중선의 교점을 [math]\displaystyle{ G }[/math]라 하자. 그리고 [math]\displaystyle{ \overline{GC} }[/math]의 연장선이 [math]\displaystyle{ \overline{AB} }[/math]와 만나는 점을 [math]\displaystyle{ F }[/math]라 하자. 체바의 정리에 의해, [math]\displaystyle{ \frac{\overline{AF}}{\overline{FB}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{CE}}{\overline{EA}}=1 }[/math]. 한편, [math]\displaystyle{ \overline{BD}=\overline{DC},\,\overline{CE}=\overline{EA} }[/math]이므로, [math]\displaystyle{ \overline{AF}=\overline{FB} }[/math].
2. [math]\displaystyle{ \triangle{ABD} }[/math]와 [math]\displaystyle{ \overline{CF} }[/math]에서 메넬라우스의 정리에 의해 [math]\displaystyle{ \frac{\overline{BF}}{\overline{FA}}\cdot\frac{\overline{AG}}{\overline{GD}}\cdot\frac{\overline{DC}}{\overline{CB}}=1 }[/math]. 한편, [math]\displaystyle{ \frac{\overline{BF}}{\overline{FA}}=1,\,\frac{\overline{DC}}{\overline{CB}}=\frac{1}{2} }[/math]이므로 [math]\displaystyle{ \frac{\overline{AG}}{\overline{GD}}=2 }[/math]. 나머지 두 중선에 대해서도 같은 방법으로 증명이 가능하다.
3. 먼저 [math]\displaystyle{ S_{\triangle{GBD}}=S_{\triangle{GCD}},\,S_{\triangle{GBF}}=S_{\triangle{GAF}},\,S_{\triangle{GAE}}=S_{\triangle{GCE}} }[/math]이다. 또한, [math]\displaystyle{ S_{\triangle{GAF}}:S_{\triangle{GAC}}=1:2 }[/math]이므로, [math]\displaystyle{ S_{\triangle{GAF}}=S_{\triangle{GAE}} }[/math]. 같은 방법으로 [math]\displaystyle{ S_{\triangle{GBF}}=S_{\triangle{GBD}} }[/math]를 보일 수 있다. 따라서 6개의 삼각형의 넓이는 모두 같다 ([math]\displaystyle{ G }[/math]가 무게중심이라 불리는 이유).
4. [math]\displaystyle{ \vec{BG} }[/math]는 [math]\displaystyle{ \overline{AD} }[/math]의 2:1 내분점이므로, [math]\displaystyle{ \vec{BG}=\frac{2\vec{BD}+\vec{BA}}{3}=\frac{\vec{BC}+\vec{BA}}{3} }[/math]. 따라서 [math]\displaystyle{ \vec{OG}=\vec{OB}+\vec{BG}=\vec{b}+\frac{\vec{c}-\vec{b}+\vec{a}-\vec{b}}{3}=\frac{\vec{a}+\vec{b}+\vec{c}}{3} }[/math]이다.
5. [math]\displaystyle{ \triangle{GAB} }[/math]에서 파푸스의 중선정리를 쓰면, [math]\displaystyle{ \overline{GA}^2+\overline{GB}^2=2\left(\overline{AF}^2+\overline{GF}^2\right)=2\left(\left(\frac{1}{2}\overline{AB}\right)^2+\left(\frac{1}{2}\overline{GC}\right)^2\right)=\frac{1}{2}\left(\overline{AB}^2+\overline{GC}^2\right) }[/math]. [math]\displaystyle{ \triangle{GBC},\,\triangle{GCA} }[/math]에 대해서도 파푸스의 중선정리를 쓴 뒤 세 식을 더하면 원하는 식이 나온다.
6. 오일러 직선 참조.
무게중심을 찾는 방법[편집 | 원본 편집]
- 삼각형의 경우에는 두 중선의 교점을 찾으면 된다.
- 평행사변형의 경우에는 두 대각선의 교점이다.
- 임의의 볼록사각형 같은 경우는, 먼저 대각선을 그어 두 삼각형으로 나눈 뒤, 각 삼각형의 무게중심을 찾는다. 그럼 그 두 무게중심을 이은 선분을 두 삼각형의 넓이의 비로 내분한 점이 무게중심.
- 원의 경우는 원의 중심이 무게중심.
- 임의의 도형의 무게중심을 찾고 싶다면, 먼저 둘레 위의 한 점을 찍은 뒤 지면에 수직하게 (= 중력가속도 방향으로) 놓는다. 그 뒤 그 점에서 수직 아래로 선을 긋는다. 둘레 위의 다른 점에서도 같은 과정을 반복한다. 이 때, 그어진 두 선의 교점이 무게중심이다.
참고로 무게중심이 도형 안에 있다는 보장은 없다. 간단하게 도넛 모양을 생각해 보면 이해가 될 듯. 볼록다각형은 무게중심이 도형 안에 있지만, 오목다각형의 경우에는 무게중심이 바깥에 있을 수도 있다.