Menelaus' Theorem
개요[편집 | 원본 편집]
그리스의 수학자이자 천문학자인 메넬라우스가 증명한 초등적 유클리드 기하학의 정리. 학교에서는 배우지 않지만, 수학 경시대회를 준비한다면 반드시 거쳐가야할 과정 중 하나. 보통 체바의 정리와 함께 배운다. 참고로 메넬라우스의 정리, 그 자체만을 사용하는 문제보다는 하나의 과정으로 사용하는 경우가 많다. 변의 길이의 비를 구하거나, 공선점 여부를 파악할 때 등.
정리[편집 | 원본 편집]
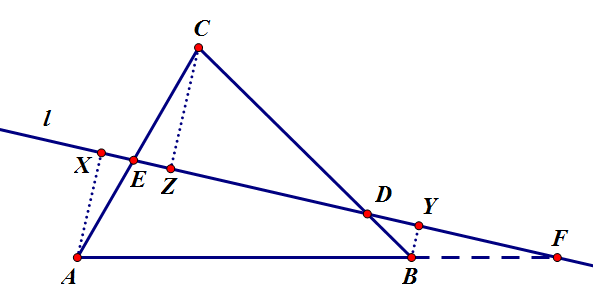
직선 [math]\displaystyle{ l }[/math]과 [math]\displaystyle{ \triangle{ABC} }[/math]의 세 변, 혹은 그 연장선과 각각 [math]\displaystyle{ D,E,F }[/math]에서 만나면, [math]\displaystyle{ \frac{\overline{AF}}{\overline{FB}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{CE}}{\overline{EA}}=1 }[/math]이 성립한다. 역으로, 한 직선과 삼각형의 세 변에 대해 위 식이 성립하면, 점 [math]\displaystyle{ D,E,F }[/math]는 공선점이다.
참고로 직선 [math]\displaystyle{ l }[/math]이 삼각형의 세 변과 만나지 않고, 연장선과만 만나도 상관없다. 하지만 증명엔 별 차이 없다.
증명[편집 | 원본 편집]
꼭짓점 [math]\displaystyle{ A,B,C }[/math]에서 직선 [math]\displaystyle{ l }[/math]에 내린 수선의 발을 각각 [math]\displaystyle{ X,Y,Z }[/math]라 하자. 그럼, [math]\displaystyle{ \triangle{AEX}\sim\triangle{CEZ},\,\triangle{CDZ}\sim\triangle{BDY},\,\triangle{BFY}\sim\triangle{AFX} }[/math]임을 쉽게 보일 수 있다 (AA 닮음). 따라서,
- [math]\displaystyle{ \frac{\overline{AF}}{\overline{FB}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{CE}}{\overline{EA}}=\frac{\overline{AX}}{\overline{BY}}\cdot\frac{\overline{BY}}{\overline{CZ}}\cdot\frac{\overline{CZ}}{\overline{AX}}=1 }[/math]
이다.
역으로 [math]\displaystyle{ \overline{DE} }[/math]의 연장선이 변 [math]\displaystyle{ \overline{AB} }[/math], 혹은 그 연장선과 만나는 점을 [math]\displaystyle{ F' }[/math]라 하면, 메넬라우스의 정리에 의해 [math]\displaystyle{ \frac{\overline{AF'}}{\overline{F'B}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{CE}}{\overline{EA}}=1 }[/math]이 성립한다. 한편, [math]\displaystyle{ \frac{\overline{AF}}{\overline{FB}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{CE}}{\overline{EA}}=1 }[/math]도 성립하므로, 두 식을 비교하면, [math]\displaystyle{ \frac{\overline{AF}}{\overline{FB}}=\frac{\overline{AF'}}{\overline{F'B}} }[/math]이다. 이는 곧, 두 점 [math]\displaystyle{ F,F' }[/math]가 선분 [math]\displaystyle{ \overline{AB} }[/math]를 같은 비로 내분/외분함을 의미한다. 즉, [math]\displaystyle{ F,F' }[/math]는 일치하고, 세 점 [math]\displaystyle{ D,E,F }[/math]는 공선점이다.
이 증명법은 가장 대표적인 증명법으로, 학원가에서는 보통 이 방법으로 가르친다. 하지만 일부 변태 수학자들은 넓이비, 벡터, 비조화비 등 다양한 방법으로 증명을 한다. 물론 초등 기하인 만큼 전부 간단하다.
삼각함수[편집 | 원본 편집]
위 그림의 [math]\displaystyle{ \triangle{AFE},\triangle{BFD},\triangle{CDE} }[/math]에 각각 사인 법칙을 적용하면,
- [math]\displaystyle{ \frac{\overline{AF}}{\overline{EA}}=\frac{\sin\angle{AEF}}{\sin\angle{EFA}},\,\frac{\overline{BD}}{\overline{FB}}=\frac{\sin\angle{DFB}}{\sin\angle{BDF}},\,\frac{\overline{CE}}{\overline{DC}}=\frac{\sin\angle{CDE}}{\sin\angle{DEC}} }[/math]
가 성립한다. 또한, [math]\displaystyle{ \sin\angle{AEF}=\sin\angle{DEC},\,\sin\angle{DFB}=\sin\angle{EFA},\,\sin\angle{CDE}=\sin\angle{BDF} }[/math]가 성립하므로, 이를 메넬라우스의 정리에 전부 대입하면,
- [math]\displaystyle{ \frac{\overline{AF}}{\overline{FB}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{CE}}{\overline{EA}}=\frac{\overline{AF}}{\overline{EA}}\cdot\frac{\overline{BD}}{\overline{FB}}\cdot\frac{\overline{CE}}{\overline{DC}}=\frac{\sin\angle{AEF}}{\sin\angle{EFA}}\cdot\frac{\sin\angle{DFB}}{\sin\angle{BDF}}\cdot\frac{\sin\angle{CDE}}{\sin\angle{DEC}}=1 }[/math]
임을 알 수 있다. 따라서, 삼각함수 버전의 메넬라우스의 정리를 얻을 수 있고, 정리하면 아래와 같다.
직선 [math]\displaystyle{ l }[/math]이 [math]\displaystyle{ \triangle{ABC} }[/math]의 세 변, 혹은 그 연장선과 각각 [math]\displaystyle{ D,E,F }[/math]에서 만나면, [math]\displaystyle{ \frac{\sin\angle{AEF}}{\sin\angle{EFA}}\cdot\frac{\sin\angle{DFB}}{\sin\angle{BDF}}\cdot\frac{\sin\angle{CDE}}{\sin\angle{DEC}}=1 }[/math]이 성립한다. 역으로 위의 식이 성립하면, [math]\displaystyle{ D,E,F }[/math]는 공선점이다.
활용[편집 | 원본 편집]
메넬라우스의 정리를 배운 학생들은 도대체 이게 어디서 활용되는지 모르는 경우가 많다. 아래는 메넬라우스의 정리를 활용한 문제의 예시로, 증명은 생략한다.