체바의 정리

Ceva's Theorem

개요

이탈리아의 수학자 지오반니 체바가 1678년에 증명한 정리. 그런데 한 책에 따르면 11세기에 사라고사의 왕이 이미 증명을 했다고 한다. 초등적인 유클리드 기하학의 정리로, 학교에서는 가르치지 않지만 수학 경시대회를 준비한다면 배우게 될 정리 중 하나. 보통 메넬라우스의 정리와 함께 배운다.

정리

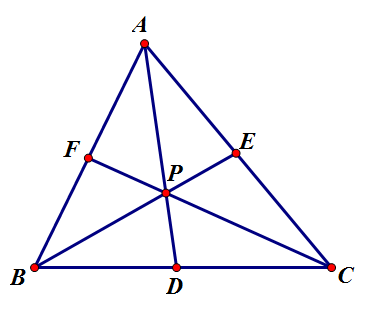
[math]\displaystyle{ \triangle{ABC} }[/math]의 세 변, 혹은 그 연장선 위에 각각 점 [math]\displaystyle{ D,E,F }[/math]를 잡는다. 세 선분 [math]\displaystyle{ \overline{AD},\overline{BE},\overline{CF} }[/math]가 한 점에서 만날 필요충분조건은 [math]\displaystyle{ \frac{\overline{AF}}{\overline{FB}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{CE}}{\overline{EA}}=1 }[/math]이다.

증명

[math]\displaystyle{ \frac{\overline{BD}}{\overline{DC}}=\frac{S_{\triangle{ABD}}}{S_{\triangle{ADC}}}=\frac{S_{\triangle{PBD}}}{S_{\triangle{PDC}}}=\frac{S_{\triangle{ABD}}-S_{\triangle{PBD}}}{S_{\triangle{ADC}}-S_{\triangle{PDC}}}=\frac{S_{\triangle{ABP}}}{S_{\triangle{CAP}}} }[/math]. 마찬가지 방법으로, [math]\displaystyle{ \frac{\overline{CE}}{\overline{EA}}=\frac{S_{\triangle{BCP}}}{S_{\triangle{ABP}}},\,\frac{\overline{AF}}{\overline{FB}}=\frac{S_{\triangle{CAP}}}{S_{\triangle{BCP}}} }[/math]. 이 세 식을 변끼리 곱하면, :[math]\displaystyle{ \frac{\overline{AF}}{\overline{FB}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{CE}}{\overline{EA}}=\frac{S_{\triangle{CAP}}}{S_{\triangle{BCP}}}\cdot\frac{S_{\triangle{ABP}}}{S_{\triangle{CAP}}}\cdot\frac{S_{\triangle{BCP}}}{S_{\triangle{ABP}}}=1 }[/math] 이다.

역으로, [math]\displaystyle{ \overline{AD},\,\overline{BE} }[/math]의 교점을 [math]\displaystyle{ P }[/math]라 하고, 직선 [math]\displaystyle{ \overleftrightarrow{CP} }[/math]가 변 [math]\displaystyle{ \overline{AB} }[/math]와 만나는 점을 [math]\displaystyle{ F' }[/math]라 하면, 체바의 정리에 의해, [math]\displaystyle{ \frac{\overline{AF'}}{\overline{F'B}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{CE}}{\overline{EA}}=1 }[/math]이다. 또한, 주어진 조건으로 부터, [math]\displaystyle{ \frac{\overline{AF}}{\overline{FB}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{CE}}{\overline{EA}}=1 }[/math]이다. 두 식을 비교하면, [math]\displaystyle{ \frac{\overline{AF'}}{\overline{F'B}}=\frac{\overline{AF}}{\overline{FB}} }[/math]이고, [math]\displaystyle{ F,F' }[/math]는 선분 [math]\displaystyle{ \overline{AB} }[/math]를 같은 비로 내분/외분한다. 따라서 [math]\displaystyle{ F=F' }[/math]이고, [math]\displaystyle{ \overline{AD},\overline{BE},\overline{CF} }[/math]는 한 점에서 만난다.

위 그림에선 점 [math]\displaystyle{ P }[/math]가 [math]\displaystyle{ \triangle{ABC} }[/math] 내부에 있는데, 외부에 있어도 성립한다.

삼각함수

세 변의 길이의 비가 아닌 각의 비로도 체바의 정리를 나타낼 수 있다. 또한, 점 [math]\displaystyle{ P }[/math]가 [math]\displaystyle{ \triangle{ABC} }[/math] 외부에 있어도 마찬가지로 성립한다.

[math]\displaystyle{ \triangle{ABC} }[/math]의 세 변, 혹은 그 연장선 위에 각각 점 [math]\displaystyle{ D,E,F }[/math]를 잡는다. 세 선분 [math]\displaystyle{ \overline{AD},\overline{BE},\overline{CF} }[/math]가 한 점에서 만날 필요충분조건은 [math]\displaystyle{ \frac{\sin\angle{ABE}}{\sin\angle{DAB}}\cdot\frac{\sin\angle{BCF}}{\sin\angle{EBC}}\cdot\frac{\sin\angle{CAD}}{\sin\angle{FCA}}=1 }[/math]이다.

증명

[math]\displaystyle{ \triangle{ABP} }[/math]에 사인 법칙을 저용하면, [math]\displaystyle{ \frac{\sin\angle{ABE}}{\sin\angle{DAB}}=\frac{\sin\angle{ABP}}{\sin\angle{PAB}}=\frac{\overline{AP}}{\overline{BP}} }[/math]이다. 같은 방법으로 [math]\displaystyle{ \triangle{BCP},\,\triangle{CAP} }[/math]에 사인 법칙을 적용하면, [math]\displaystyle{ \frac{\sin\angle{BCF}}{\sin\angle{EBC}}=\frac{\overline{BP}}{\overline{CP}},\,\frac{\sin\angle{CAD}}{\sin\angle{FCA}}=\frac{\overline{CP}}{\overline{AP}} }[/math]이다. 이 세 식을 변끼리 곱하면,

[math]\displaystyle{ \frac{\sin\angle{ABE}}{\sin\angle{DAB}}\cdot\frac{\sin\angle{BCF}}{\sin\angle{EBC}}\cdot\frac{\sin\angle{CAD}}{\sin\angle{FCA}}=\frac{\overline{AP}}{\overline{BP}}\cdot\frac{\overline{BP}}{\overline{CP}}\cdot\frac{\overline{CP}}{\overline{AP}}=1 }[/math]이다.

역으로, 주어진 식이 성립한다 가정하자. [math]\displaystyle{ \triangle{ABD},\,\triangle{ACD} }[/math]에 사인 버빅을 적용하면, [math]\displaystyle{ \frac{\overline{AB}}{\overline{BD}}=\frac{\sin\angle{ADB}}{\sin\angle{DAB}},\,\frac{\overline{DC}}{\overline{CA}}=\frac{\sin\angle{CAD}}{\sin\angle{ADC}} }[/math]이다. 또한, [math]\displaystyle{ \angle{ADC}+\angle{ADB}=180^\circ }[/math]이므로, [math]\displaystyle{ \sin\angle{ADB}=\sin\angle{ADC} }[/math]이다. 따라서, [math]\displaystyle{ \frac{\overline{DC}}{\overline{BD}}\cdot\frac{\overline{AB}}{\overline{CA}}=\frac{\sin\angle{CAD}}{\sin\angle{DAB}} }[/math]. 같은 방법으로, [math]\displaystyle{ \frac{\overline{AE}}{\overline{EC}}\cdot\frac{\overline{BC}}{\overline{AB}}=\frac{\sin\angle{ABE}}{\sin\angle{EBC}},\,\frac{\overline{BF}}{\overline{FA}}\cdot\frac{\overline{CA}}{\overline{BC}}=\frac{\sin\angle{BCF}}{\sin\angle{FCA}} }[/math]이다. 이 세 식을 변끼리 곱하면,

[math]\displaystyle{ \frac{\overline{BF}}{\overline{FA}}\cdot\frac{\overline{DC}}{\overline{BD}}\cdot\frac{\overline{EA}}{\overline{CE}}=\frac{\overline{DC}}{\overline{BD}}\cdot\frac{\overline{AB}}{\overline{CA}}\cdot\frac{\overline{AE}}{\overline{EC}}\cdot\frac{\overline{BC}}{\overline{AB}}\cdot\frac{\overline{BF}}{\overline{FA}}\cdot\frac{\overline{CA}}{\overline{BC}}=\frac{\sin\angle{CAD}}{\sin\angle{DAB}}\cdot\frac{\sin\angle{ABE}}{\sin\angle{EBC}}\cdot\frac{\sin\angle{BCF}}{\sin\angle{FCA}}=1 }[/math]

이다. 곧, [math]\displaystyle{ \frac{\overline{AF}}{\overline{FB}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{CE}}{\overline{EA}}=1 }[/math]이고, 체바의 정리의 역에 의해 [math]\displaystyle{ \overline{AD},\overline{BE},\overline{CF} }[/math]는 한 점에서 만난다.

활용

체바의 정리를 어떻게 활용하냐고 물을 수 있는데, 이 정리는 주로 길이의 비를 구하거나, 세 직선이 한 점에서 만나는지 아닌지 확인하는 데 쓰인다. 대표적으로 삼각형의 세 중선이 한 점에서 만남을 한 줄로 증명할 수 있으며, 비슷한 방법으로 세 수선, 세 내각의 이등분선이 한 점에서 만남을 증명할 수 있다.

관련 항목

• 삼각형
• 메넬라우스의 정리