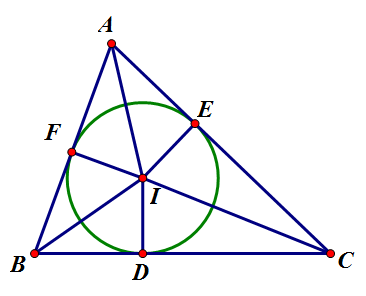
Incenter
정의[편집 | 원본 편집]
다각형의 내접원의 중심을 부르는 말. 하지만 보통 내심이라고 하면 삼각형의 내접원의 중심만을 이른다. 어떤 다각형의 내심, 즉 내접원이 존재하기 위한 조건은 모든 변까지의 거리가 동일한 점이 존재하면 된다. 만약 그런 점이 존재할 경우, 그 점이 내심이 되며, 내심과 어떤 한 변까지의 거리가 내접원의 반지름이 된다. 참고로 이 조건은 모든 각의 이등분선이 한 점에서 만난다와 동치인 명제이다.
삼각형의 경우에는 반드시 내심이 존재하며, 사각형 부터는 존재할 수도 있고 존재하지 않을 수도 있다. 사실 내접원 자체가 외접원에 비해서 약간 홀대를 받는 느낌이다. 당장 공원점에는 여러 조건이 존재하지만 내접원에 관한 조건은 몇 개 없다.안습
내접원만의 성질[편집 | 원본 편집]
- 삼각형의 각의 이등분선은 반드시 한 점에서 만난다.
- 내접원의 반지름을 [math]\displaystyle{ r }[/math]이라 했을 때, 삼각형의 넓이는 [math]\displaystyle{ \frac{1}{2}r\left(a+b+c\right) }[/math]이다.
- [math]\displaystyle{ \overline{BC}=\alpha,\,\overline{AC}=\beta,\,\overline{AB}=\gamma }[/math]라 하고 각 꼭짓점까지의 벡터를 [math]\displaystyle{ \vec{a},\,\vec{b},\,\vec{c} }[/math]라 했을 때, 내심의 벡터는 [math]\displaystyle{ \frac{\alpha\vec{a}+\beta\vec{b}+\gamma\vec{c}}{\alpha+\beta+\gamma} }[/math]이다.
- 내접원은 삼각형의 세 변에 모두 접한다.
- 각 꼭짓점에서 내접원에 그은 접선의 길이는 각각 [math]\displaystyle{ s-a,s-b,s-c }[/math]이다 (단, [math]\displaystyle{ s=\frac{a+b+c}{2} }[/math]는 둘레의 절반).
증명[편집 | 원본 편집]
1.[math]\displaystyle{ \angle{A} }[/math]와 [math]\displaystyle{ \angle{B} }[/math]의 이등분선의 교점을 [math]\displaystyle{ I }[/math]라 하자. 또한, [math]\displaystyle{ I }[/math]에서 각변에 내린 수선의 발을 [math]\displaystyle{ D,E,F }[/math]라 하자. 그러면 [math]\displaystyle{ \triangle{IAE}\cong\triangle{IAF},\,\triangle{IBF}\cong\triangle{IBD} }[/math](RHA 합동)이다. 따라서 [math]\displaystyle{ \overline{IE}=\overline{IF}=\overline{ID} }[/math]이다. 한편, [math]\displaystyle{ \angle{IEC}=\angle{IDC}=\angle{R},\,\overline{IC} }[/math] 공통 이므로 [math]\displaystyle{ \triangle{ICE}\cong\triangle{ICD} }[/math](RHS 합동)이다. 따라서 [math]\displaystyle{ \angle{ICE}=\angle{ICD} }[/math]이다.
2. [math]\displaystyle{ S_{\triangle{ABC}}=S_{\triangle{AIB}}+S_{\triangle{BIC}}+S_{\triangle{CIA}}=\frac{1}{2}\left(ar+br+cr\right)=\frac{1}{2}r\left(a+b+c\right) }[/math].
3.각 [math]\displaystyle{ A }[/math]의 이등분선이 [math]\displaystyle{ \overline{BC} }[/math]와 만나는 점을 [math]\displaystyle{ P }[/math]라 하자. 그럼[math]\displaystyle{ \vec{AP} }[/math]는 [math]\displaystyle{ \vec{AB},\vec{AC} }[/math]를 [math]\displaystyle{ \gamma:\beta }[/math]로 내분한 벡터이다. 따라서 [math]\displaystyle{ \vec{AP}=\frac{\gamma\vec{AC}+\beta\vec{AB}}{\beta+\gamma} }[/math]. 한편, [math]\displaystyle{ \left\|\vec{BP}\right\| }[/math]는 각의 이등분선 정리에 의해 [math]\displaystyle{ \frac{\gamma\alpha}{\beta+\gamma} }[/math]이다. 내심 [math]\displaystyle{ I }[/math]는 [math]\displaystyle{ \vec{AP} }[/math] 위에 있고, 길이의 비는 다시 한번 각의 이등분선 정리에 의해 [math]\displaystyle{ \frac{\gamma}{\gamma+\left\|\vec{BP}\right\|}=\frac{\beta+\gamma}{\alpha+\beta+\gamma} }[/math]이다. 따라서 [math]\displaystyle{ \vec{AI}=\frac{\beta+\gamma}{\alpha+\beta+\gamma}\times\vec{AP}=\frac{\gamma\vec{AC}+\beta\vec{AB}}{\alpha+\beta+\gamma} }[/math]이다. 이제 [math]\displaystyle{ \vec{OI}=\vec{OA}+\vec{AI}=\vec{a}+\vec{AI},\,\vec{AC}=\vec{c}-\vec{a},\,\vec{AB}=\vec{b}-\vec{a} }[/math]를 이용하여 정리하면 [math]\displaystyle{ \vec{OI}=\frac{\alpha\vec{a}+\beta\vec{b}+\gamma\vec{c}}{\alpha+\beta+\gamma} }[/math]이다.
4. 생략
5. 한 꼭짓점에서 원에 그은 접선의 길이는 같다는 성질을 사용한다. [math]\displaystyle{ \overline{AF}=x }[/math]라 두자. 그럼 [math]\displaystyle{ \overline{FB}=\overline{BD}=c-x,\,\overline{DC}=\overline{CE}=a-\left(c-x\right)=a-c+x,\,\overline{AE}=b-\left(a-c+x\right)=b-a+c-x=x }[/math]. 이 식을 [math]\displaystyle{ x }[/math]에 관해 풀면, [math]\displaystyle{ x=\frac{-a+b+c}{2}=s-a }[/math]이다. 다른 접선에 대해서도 같은 방법으로 증명이 가능하다.
기타 성질[편집 | 원본 편집]
- 기하학에서의 오일러의 정리에 따르면 외심과 내심 사이의 거리는 [math]\displaystyle{ \sqrt{R\left(R-2r\right)} }[/math]이다 ([math]\displaystyle{ R }[/math]은 외접원의 반지름). 여기서 내접원의 반지름은 외접원의 반지름의 길이의 절반 이하라는 사실을 알 수 있다. 등호는 외심과 내심이 일치할 때 성립한다.
- 사각형의 내심이 존재할 조건은 항목을 참조하자.
- 내접원은 구점원과 접한다 (포이어바흐 정리). 또한, 내접원과 구점원의 접점을 포이어바흐 점이라 부른다.
- 방접원의 반지름을 [math]\displaystyle{ r_a,r_b,r_c }[/math]라 하면, [math]\displaystyle{ \frac{1}{r}=\frac{1}{r_a}+\frac{1}{r_b}+\frac{1}{r_c} }[/math]가 성립한다. 증명은 방심 참조.