Excenter
정의[편집 | 원본 편집]
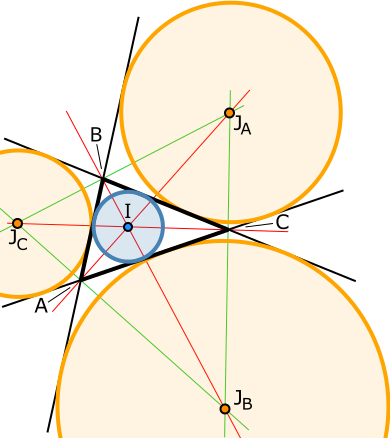
삼각형의 오심 중 하나로, 한 내각의 이등분선과 다른 두 외각의 이등분선의 교점을 부르는 말이다. 다만, 삼각형의 다른 중심과는 달리 방심은 어떤 내각을 고르냐에 따라 서로 다른 3개의 방심이 존재한다. 방심은 기호로 [math]\displaystyle{ I_A }[/math] 혹은 [math]\displaystyle{ J_A }[/math]를 사용하며, 수심과 마찬가지로 한국의 수학 교육과정에서는 어째서인지 다루지 않는다. 하지만 수학 경시대회를 준비한다면 반드시 알아야하는 개념 중 하나이며, 방접원의 여러 성질들을 공부하는 것도 중요하다.
성질[편집 | 원본 편집]
- 삼각형의 한 내각과 다른 두 외각은 반드시 한 점에서 만난다.
- 방접원은 삼각형의 한 변과 다른 두 변의 연장선과 접한다.
- 방접원의 반지름을 각각 [math]\displaystyle{ r_a,r_b,r_c }[/math]라 하면, [math]\displaystyle{ S_{\triangle{ABC}}=\left(s-a\right)r_a=\left(s-b\right)r_b\left(s-c\right)r_c }[/math]이다. 단, [math]\displaystyle{ s=\frac{a+b+c}{2} }[/math]이다.
- 내접원의 반지름을 [math]\displaystyle{ r }[/math]이라 하면 [math]\displaystyle{ S_{\triangle{ABC}}=\sqrt{rr_ar_br_c} }[/math]이다.
- [math]\displaystyle{ \frac{1}{r}=\frac{1}{r_a}+\frac{1}{r_b}+\frac{1}{r_c} }[/math]이다.
- 내접원의 중심을 [math]\displaystyle{ I }[/math]라 하면, [math]\displaystyle{ A,I,J_A }[/math]는 공선점이다.
- [math]\displaystyle{ J_A,C,J_B }[/math]는 공선점이다.
- [math]\displaystyle{ \triangle{J_AJ_BJ_C} }[/math]의 수심은 [math]\displaystyle{ I }[/math]이다.
- 세 방접원은 모두 구점원과 접한다.
증명[편집 | 원본 편집]
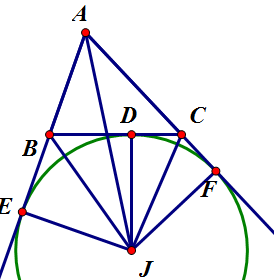
1. [math]\displaystyle{ \angle{A} }[/math]의 이등분선과 [math]\displaystyle{ B }[/math]의 외각의 이등분선이 만나는 점을 [math]\displaystyle{ J }[/math]라 하자. 그리고 [math]\displaystyle{ J }[/math]에서 각 변에 내린 수선의 발을 [math]\displaystyle{ D,E,F }[/math]라 하자. 그럼 [math]\displaystyle{ \angle{BEJ}=\angle{BDJ}=90^\circ,\,\angle{JBE}=\angle{JBD},\,\overline{BJ} }[/math] 공통이므로 [math]\displaystyle{ \triangle{BEJ}\cong\triangle{BDJ} }[/math](RHA 합동)이다. 따라서 [math]\displaystyle{ \overline{JE}=\overline{JD} }[/math]. 같은 방법으로 [math]\displaystyle{ \triangle{AEJ}\cong\triangle{AFJ} }[/math](RHA 합동)이고, 따라서 [math]\displaystyle{ \overline{JE}=\overline{JF} }[/math]이다. 따라서 [math]\displaystyle{ \overline{JD}=\overline{JF},\,\angle{JDC}=\angle{JFC}=90^\circ,\,\overline{JC} }[/math] 공통이므로, [math]\displaystyle{ \triangle{JDC}\cong\triangle{JFC} }[/math]이고, 곧 [math]\displaystyle{ \angle{JCD}=\angle{JCF} }[/math]이다.
이제 [math]\displaystyle{ \angle{B},\,\angle{C} }[/math]의 외각의 이등분선이 만나는 점을 [math]\displaystyle{ J }[/math]라 하자. 위와 비슷한 방법으로 [math]\displaystyle{ \angle{JAB}=\angle{JAC} }[/math]를 증명할 수 있다.
2. (생략)
3. [math]\displaystyle{ S_{\triangle{ABC}}=S_{\triangle{ABJ}}+S_{\triangle{ACJ}}-S_{\triangle{BCJ}}=\frac{1}{2}cr_a+\frac{1}{2}br_a-\frac{1}{2}ar_a=\frac{1}{2}\left(b+c-a\right)r_a=\left(s-a\right)r_a }[/math]이다. 나머지 방심에 대해서도 같은 방법으로 증명이 가능하다.
4. 내접원의 성질에서, [math]\displaystyle{ S=rs }[/math]이다 ([math]\displaystyle{ S=S_{\triangle{ABC}} }[/math]). 따라서 [math]\displaystyle{ r^2=\frac{S^2}{s^2}=\frac{\left(s-a\right)\left(s-b\right)\left(s-c\right)}{s} }[/math]이다 (헤론의 공식). 한편, 3번 성질에서 같은 방법으로 [math]\displaystyle{ {r_a}^2=\frac{s\left(s-b\right)\left(s-c\right)}{s-a} }[/math]이다. 나머지 방접원에 대해서도 같은 방법으로 해준 뒤, 식을 변끼리 곱하면, [math]\displaystyle{ \left(rr_ar_br_c\right)^2=\left(s\left(s-a\right)\left(s-b\right)\left(s-c\right)\right)^2=S^2 }[/math]이다 (헤론의 공식). 따라서 [math]\displaystyle{ S=\sqrt{rr_ar_br_c} }[/math].
5. [math]\displaystyle{ S=\left(s-a\right)r_a=\left(s-b\right)r_b\left(s-c\right)r_c=rs }[/math]에서, [math]\displaystyle{ \frac{r}{r_a}=\frac{s-a}{s},\,\frac{r}{r_b}=\frac{s-b}{s},\,\frac{r}{r_c}=\frac{s-c}{s} }[/math]이다. 이 세 식을 변끼리 더하면, [math]\displaystyle{ \frac{r}{r_a}+\frac{r}{r_b}+\frac{r}{r_c}=\frac{3s-a-b-c}{s}=\frac{3s-2s}{s}=1 }[/math]. 양변을 [math]\displaystyle{ r }[/math]로 나눠주면 [math]\displaystyle{ \frac{1}{r}=\frac{1}{r_a}+\frac{1}{r_b}+\frac{1}{r_c} }[/math]이다.
6. 각 각도를 [math]\displaystyle{ a,b,c }[/math]라 하자. 그럼 [math]\displaystyle{ a+b+c=180^\circ }[/math]이다. [math]\displaystyle{ I }[/math]는 세 내각의 이등분선의 교점이므로, [math]\displaystyle{ \angle{IAB}=a/2,\,\angle{IBA}=b/2 }[/math]이고, 따라서 [math]\displaystyle{ \angle{AIB}=180^\circ-\left(a+b\right)/2 }[/math]이다. 한편, [math]\displaystyle{ \angle{J_ABC} }[/math]는 [math]\displaystyle{ B }[/math]의 외각의 절반이므로, [math]\displaystyle{ \angle{J_ABC}=\left(a+c\right)/2 }[/math]이다. 따라서 [math]\displaystyle{ \angle{IBJ_A}=b/2+\left(a+c\right)/2=\left(a+b+c\right)/2=90^\circ }[/math]. 같은 방법으로 [math]\displaystyle{ \angle{ICJ_A}=90^\circ }[/math]이다. 따라서 점 [math]\displaystyle{ B,I,C,J_A }[/math]는 (공원점)이고, [math]\displaystyle{ \angle{BIJ_A}=\angle{BCJ_A} }[/math]이다 (원주각). 한편, [math]\displaystyle{ \angle{BCJ_A} }[/math]는 각 [math]\displaystyle{ C }[/math]의 외각의 절반이므로, [math]\displaystyle{ \angle{BCJ_A}=\left(a+b\right)/2 }[/math]. 따라서 [math]\displaystyle{ \angle{AIB}+\angle{BIJ_A}=180^\circ-\left(a+b\right)/2+\left(a+b\right)/2=180^\circ }[/math]. 이는 곧 [math]\displaystyle{ A,I,J_A }[/math]가 공선점임을 의미한다.
7. 6번 성질의 증명 과정 중, [math]\displaystyle{ \angle{ICJ_A}=90^\circ }[/math]임을 보였다. 같은 방법으로 [math]\displaystyle{ \angle{ICJ_B}=90^\circ }[/math]이고, 따라서 [math]\displaystyle{ \angle{ICJ_B}+\angle{ICJ_A}=180^\circ }[/math]이다. 이는 곧 [math]\displaystyle{ J_B,C,J_A }[/math]가 공선점임을 의미한다.
8. 6번과 7번 성질의 따름정리. 증명은 생략한다.
9. 포이어바흐 정리 참조.
기타[편집 | 원본 편집]
위에 나열된 성질 외에도, 중학교에선 가르치기에 곤란한 정신나간 성질들이 많다. 그런데 그 많은 성질들이 순수한 수학적 흥미 외에는 영 쓸모가 없다. 학교에서 가르치지 않는 대표적인 이유. 입시위주교육의 폐해