거리공간

정의

\(X\)를 집합이라 하고 \(d\)를 [math]\displaystyle{ X\times X }[/math]로부터 0 이상의 실수의 집합 [math]\displaystyle{ \mathbb{R}^+ }[/math]로의 함수라고 하자. 임의의 [math]\displaystyle{ x,y,z\in X }[/math]에 대해 다음 조건

(1) [math]\displaystyle{ d(x,y)=0 \Leftrightarrow x=y }[/math]

(2) [math]\displaystyle{ d(x,y)=d(y,x) }[/math]

(3) [math]\displaystyle{ d(x,z)\le d(x,y)+d(y,z) }[/math] (삼각부등식)

을 만족하면 [math]\displaystyle{ d:X\times X\to \mathbb{R}^+ }[/math]를 X 위의 거리(metric), 또는 거리함수(distance function)라고 한다. 그리고 [math]\displaystyle{ d(x,y) }[/math]를 x에서 y까지의 거리(distance)라고 한다.뭐여 함수도 거리라며 거리함수 d가 주어진 집합 X는 거리공간(metric space)이라고 하고 [math]\displaystyle{ (X,d) }[/math]라고 표기한다.

참고로 영어 단어 metric과 distance는 모두 "거리"라고 번역되는데, 엄밀하게 따지면 distance는 거리 값을 나타내는 스칼라, metric은 미분기하학적 측면에선 텐서이다.

예시

• [math]\displaystyle{ \mathbb{R}^n }[/math]에서 [math]\displaystyle{ \mathbf{x}=(x_1,x_2,\cdots, x_n),\mathbf{y}=(y_1,y_2,\cdots,y_n) }[/math]라 하면 \((\mathbb{R}^n,d_2),(\mathbb{R}^n,d_1),(\mathbb{R}^n,d_\infty)\)는 거리공간이다. 이때
  • [math]\displaystyle{ d_2(\mathbf{x},\mathbf{y})=\sqrt{\sum_{i=1}^n (x_i-y_i)^2} }[/math]
  • [math]\displaystyle{ d_1(\mathbf{x},\mathbf{y})=\sum_{i=1}^n|x_i-y_i| }[/math]
  • [math]\displaystyle{ d_\infty(\mathbf{x},\mathbf{y})=\max\{|x_i-y_i|: i=1,2,\cdots, n\} }[/math]
• 임의의 집합 \(X\)의 원소 \(x,y\)에 대해 [math]\displaystyle{ d(x,y)=\begin{cases} 1, &x\ne y\\ 0, &x=y \end{cases} }[/math]로 정의하자. 그러면 [math]\displaystyle{ (X,d) }[/math]는 거리공간이다.

점과 집합 사이의 거리

\((X,d)\)를 거리공간이라 하고, \(A\)는 \(X\)의 공집합이 아닌 부분집합이며, \(x\)는 \(X\)의 원소라고 하자. \(x\)에서 \(A\)까지의 거리 \(d(x,A)\)는

[math]\displaystyle{ d(x,A)=\sup\{d(x,y): y\in A\} }[/math]

로 정의한다.

지름

이와 관련한 내용은 지름에서 볼 수 있습니다.

\((X,d)\)가 거리공간이고 \(A\)를 \(X\)의 공집합이 아닌 부분집합이라고 하자. 만약 \(\{d(x,y):x,y\in A\}\)가 상계를 가지면 \(A\)를 유계집합(bounded set)이라고 하며

[math]\displaystyle{ \sup\{d(x,y):x,y\in A\} }[/math]

를 \(A\)의 지름(diameter)이라고 한다. 공집합의 지름은 0으로 정의한다. 만약 \(X\)가 유계이면, \((X,d)\)를 유계거리공간이라고 한다.

열린 집합과 닫힌 집합

거리공간 \(X,d\)에서 \(a\in X\), \(r > 0\)이 주어졌다고 하자. 다음 집합

[math]\displaystyle{ B_d(a, r)=\{ x\in X : d(x,a)\lt r\} }[/math]

을 중심이 \(a\)이고 반지름이 \(r\)인 열린 공(open ball)이라고 한다. 그리고 집합

[math]\displaystyle{ B_d[a, r]=\{ x\in X : d(x,a)\le r\} }[/math]

을 중심이 \(a\)이고 반지름이 \(r\)인 닫힌 공(open ball)이라고 한다. 거리함수를 하나만 다루어 혼동을 일으킬 염려가 없다면 단순히 \(B(a,r), B[a,r]\)로 표기한다.

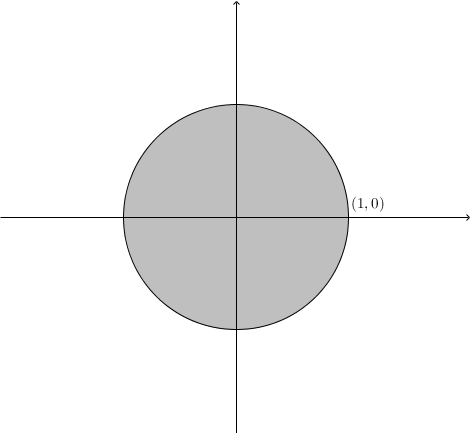
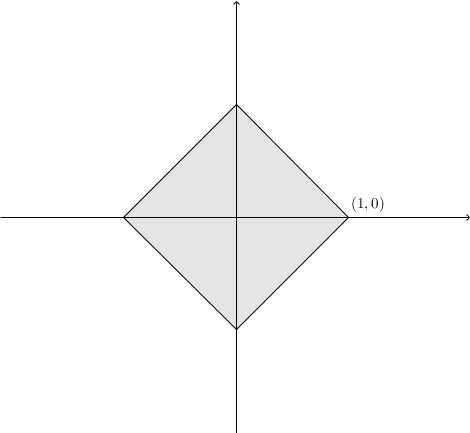
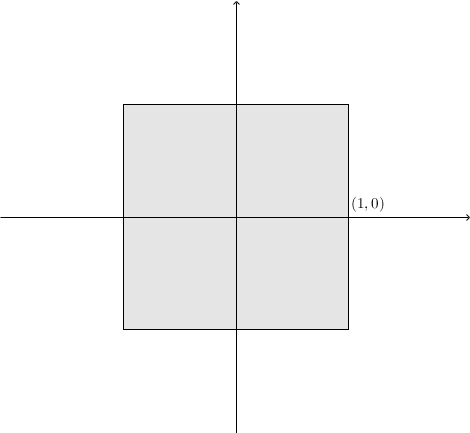
\((\mathbb{R}^2,d)\)에서 \(d\)의 정의에 따라 공 \(B(\mathbf{0},1)\)의 모습이 달라지는 것을 관찰해보자.

보통거리 [math]\displaystyle{ d(\mathbf{a},\mathbf{b})=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2} }[/math]	택시거리 [math]\displaystyle{ d(\mathbf{a},\mathbf{b})=|a_1-b_1|+|a_2-b_2| }[/math]
최댓값거리 [math]\displaystyle{ d(\mathbf{a},\mathbf{b})=\max\{|a_1-b_1|,|a_2-b_2|\} }[/math]	이산거리 [math]\displaystyle{ d(\mathbf{a},\mathbf{b})=\begin{cases} 0, &\mathbf{a}=\mathbf{b}\\ 1, &\mathbf{a}\ne\mathbf{b} \end{cases} }[/math]

만약 \((X,d)\)의 부분집합 \(O\)가 열린 공의 합집합으로 주어지면 \(O\)를 거리함수 \(d\)에 대해 열린 집합이라고 한다. 그리고 \((X,d)\)의 부분집합 \(C\)에 대해 \(X\setminus C\)가 \(d\)에 대해 열린 집합이면 \(C\)를 \(d\)에 대해 닫힌 집합이라고 한다.

거리공간 \((X,d)\)에서 다음 성질이 성립한다.

• \(X\)와 \(\emptyset\)은 열린 집합이다.
• 열린 집합의 합집합은 열린 집합이다.
• 유한 개 열린 집합의 교집합은 열린 집합이다.

수열의 극한

이와 관련한 내용은 수열의 극한에서 볼 수 있습니다.

[math]\displaystyle{ (X,d) }[/math]가 거리공간이고 [math]\displaystyle{ (x_n) }[/math]을 X의 점열이라고 하자. 임의의 실수 [math]\displaystyle{ \varepsilon \gt 0 }[/math]에 대해 적당한 [math]\displaystyle{ N\in \mathbb{N} }[/math]이 존재하여 모든 [math]\displaystyle{ n \gt N \left(n\in\mathbb{N}\right) }[/math]에 대해 [math]\displaystyle{ d \left( x_n , x \right) \lt \varepsilon }[/math]일 때, [math]\displaystyle{ (x_n) }[/math]은 x에 수렴한다고 한다.

거리공간에서 수렴하는 수열의 극한값은 유일하다. \(X\)에서 수렴하는 수열 \((x_n)\)의 극한값을 \(\alpha,\beta\)라고 하자. 그러면 임의의 \(\varepsilon > 0\)에 대해 적당한 \(N_1, N_2 \in \mathbb{N}\)이 존재해 모든 \( n > \max\{N_1,N_2\}\)에 대해 \(d (x_n, \alpha) < \frac{\varepsilon}{2}\)이고 \(d (x_n,\beta)<\frac{\varepsilon}{2}\)이다. 그러면 거리함수의 정의에 의해

[math]\displaystyle{ d(\alpha,\beta) \le d(\alpha, x_n)+d(x_n,\beta) \lt \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon }[/math]

이다. \(\varepsilon\)이 임의의 양수이므로 \(d(\alpha,\beta)=0\), 즉 \(\alpha=\beta\)임을 안다.

연속함수

이와 관련한 내용은 연속함수에서 볼 수 있습니다.

\(f:(X,d)\to (Y,d')\)를 거리공간 \((X,d)\)에서 \((Y,d')\)로의 함수이고, [math]\displaystyle{ a\in X }[/math]라고 하자. 이때 임의의 [math]\displaystyle{ \varepsilon \gt 0 }[/math]에 대해 [math]\displaystyle{ \delta \gt 0 }[/math]이 존재해 임의의 [math]\displaystyle{ x\in X }[/math]에 대해 [math]\displaystyle{ d(x,a)\lt \delta }[/math]이면 [math]\displaystyle{ d(f(x),f(a))\lt \varepsilon }[/math]일 때, \(f\)는 \(a\)에서 연속이라고 한다.

동등한 거리공간

거리동형

이와 관련한 내용은 등거리사상에서 볼 수 있습니다.

거리공간 \((X,d), (Y,d')\)에 대해 일대일 대응 \(f:X\to Y\)가 존재해 임의의 \(a,b\in X\)에 대해

[math]\displaystyle{ d(a,b)=d'(f(a),f(b)) }[/math]

이면 \((X,d), (Y,d')\)는 거리동형(metrically equivalent) 또는 등거리(isometric)라고 하고, \(f\)는 등거리사상(isometry)이라고 한다.

위상동형

이와 관련한 내용은 위상동형사상에서 볼 수 있습니다.

거리공간 \((X,d), (Y,d')\)에 대해 일대일 대응 [math]\displaystyle{ f:X\to Y }[/math]가 존재해 \(f\)와 그 역함수 \(f^{-1}\)이 연속이면 [math]\displaystyle{ X,Y }[/math]는 위상적으로 동치(topologically equivalent), 또는 위상동형(homeomorphic)이라고 하고, f는 위상동형사상(homeomorphism)이라고 한다.

완비거리공간

이와 관련한 내용은 완비거리공간에서 볼 수 있습니다.

거리공간 \((X,d)\)에서 \(X\)의 모든 코시수열이 \(X\)의 점으로 수렴하면 \((X,d)\)를 완비거리공간(complete metric space)이라고 한다.

위상적 성질

거리공간은 다음 위상적 성질을 가진다.

• 모든 거리공간은 제1가산공간이다.

거리공간 \((X,d)\)의 임의의 점 \(a\)에서 열린 공의 모임

[math]\displaystyle{ \mathcal{B}_a=\left\{B\left(a,\frac{1}{n}\right): n\in \mathbb{N}\right\} }[/math]

이 가산집합이고 \(a\)가 \(\mathcal{B}_a\)의 임의의 원소의 원소임은 명백하다. 이제 \(a\)를 포함하는 열린 집합 \(O\)를 하나 생각하자. \(O\)가 열린 집합이므로, \(B(a,\varepsilon)\)가 \(O\)의 부분집합이 되도록 하는 \(\varepsilon>0\)이 존재한다. 그러면 아르키메데스의 원리에 의해 \(n >\frac{1}{\varepsilon}\)인 자연수 \(n\)이 존재하고

[math]\displaystyle{ B\left(a,\frac{1}{n}\right) \subseteq B(a,\varepsilon)\subseteq O }[/math]

이다. 따라서 \(\mathcal{B}_a\)가 가산국소기저이므로 원하는 결론을 얻는다.

• 모든 거리공간은 하우스도르프 공간이다.

거리공간 \((X,d)\)의 임의의 원소 \(a,b\)에 대해 열린 공 \(B\left(a,\frac{1}{2}d(a,b)\right),B\left(b,\frac{1}{2}d(a,b)\right)\)을 설정하면 두 집합은 각각 \(a,b\)를 포함하고 서로소이다. 따라서 원하는 결론을 얻는다.

• 분해가능한 거리공간은 제2가산공간이다.

같이 보기

• 택시 기하학

참고문헌

• Croom, F. (1989). Principles of topology. Philadelphia: Saunders College Pub. ISBN 9812432884