Taxicab Geometry.
택시 기하학은 19세기 헤르만 민코프스키가 고안한 비유클리드 기하학의 일종으로, 거리 함수를 유클리드 기하학의 것과 다르게 정리한 것이다.
택시 기하학은 가장 간단한 비유클리드 기하학이라고도 불린다. 꽤나 간단하고 재밌어서, 유클리드 기하학에 절어버린(...) 사고를 넓히는데 도움이 된다.
택시 거리[편집 | 원본 편집]
택시 거리는 택시 기하학에서 사용하는 거리 함수로, 맨해튼 거리(Manhattan distance), L1 거리라고도 한다.
유클리드 기하학에선 점 [math]\displaystyle{ A(x_1,y_1), B(x_2,y_2) }[/math] 사이의 거리를 [math]\displaystyle{ \sqrt{(x_2-x_1)^2 + (y_2 - y_1)^2} }[/math]으로 정의한다. 이것은 피타고라스 정리에서 쉽게 얻을 수 있는, 두 점 사이를 잇는 선분의 길이를 나타낸다.
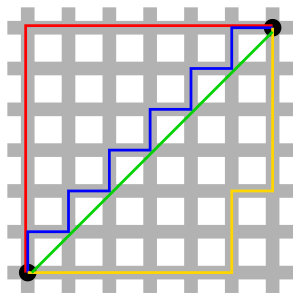
그런데, 빌딩이 빼곡하게 들어서 있고 도로가 격자로 나 있는 도시를 생각해 보자. 어떤 지점에서 다른 지점으로 갈 때, 직선 거리로 이동할 수 있을까? 건물들을 피해 도로로 이동해야 할 것이다. 이때 이동하는 거리가 바로 택시 거리이다.
옆의 그림에서 초록색(좌하단에서 우상단을 잇는 대각선)을 제외한 나머지 선들이 모두 택시 거리를 나타낸다. 즉, 가로 위치의 차와 세로 위치의 차의 합이 바로 그 거리가 되는데, 이를 수학적으로 기술하자면 다음과 같다.
[math]\displaystyle{ |x_2 - x_1| + |y_2 - y_1| }[/math]
택시 기하학에서의 도형[편집 | 원본 편집]
이렇게 거리를 다르게 정의하면 무슨 일이 일어날까?
원[편집 | 원본 편집]
원은 한 점에서 거리가 일정한 점들의 집합으로 정의된다. 유클리드 기하학에서 이 정의에 따라 원을 그리면 흔히 아는 그 동그라미가 된다. 하지만 택시 기하학에서는 거리의 정의가 다르기 때문에, 원의 모양도 변한다. 택시 기하학에서의 원을 좌표 평면에 표시해 보면 다음과 같은 정사각형이 된다.
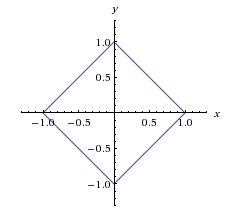
이는 [math]\displaystyle{ |x| + |y| = 1 }[/math]의 그래프이고, 유클리드 기하학에서의 원인 [math]\displaystyle{ x^2 + y^2 = 1 }[/math]에 대응한다.
[math]\displaystyle{ (x_1, y_1) }[/math]를 중심으로 하고, [math]\displaystyle{ r }[/math]을 반지름으로 하는 택시원의 방정식은 다음과 같다.
[math]\displaystyle{ |x-x_1| + |y-y_1| = r }[/math]
이것은 원의 정의에서 쉽게 알 수 있는데, 중심 [math]\displaystyle{ (x_1, y_1) }[/math]과 어떤 점 [math]\displaystyle{ (x, y) }[/math] 사이의 택시 거리가 [math]\displaystyle{ |x-x_1| + |y-y_1| }[/math]이고, 중심에서 떨어진 거리가 곧 반지름 [math]\displaystyle{ r }[/math]이기 때문이다.
앞에서 말한 바둑판 격자 모양의 도시에서 요금이 이동 거리에만 비례하는 택시가 있다고 하고, 한 곳에서 요금이 같이 나오는 도착지를 모으면 바로 택시원의 모양이 될 것이다.
포물선[편집 | 원본 편집]
포물선은 한 직선과 한 정점으로부터 같은 거리에 있는 점들의 집합으로 정의된다.