수열의 극한

극한이라는 개념은 제논의 역설에서 알 수 있듯이 고대부터 존재해왔다. 당시에 사용된 극한의 예는 원에 내접, 외접하는 다각형의 넓이를 사용해 원의 넓이를 추정한 것 등이 있다. 그 후, 세월이 흘러 뉴턴이 미적분학을 연구, 발표하면서 직관에 의존하는 극한의 개념을 이끌어 낸다. 당시로서는 극한값을 구하는 것에만 치중하였고, 수학적으로 엄밀한 연구는 하지 않았다. 현대에 쓰이는 [math]\displaystyle{ \displaystyle \displaystyle \varepsilon\text{-}N }[/math] 논법은 볼차노와 바이어슈트라스에 의해 완성된 것이다.

정의

엄밀하지 않은 정의

실수열 [math]\displaystyle{ \displaystyle \displaystyle (a_n) }[/math]이 주어졌다고 하자. n이 커질수록 [math]\displaystyle{ \displaystyle \displaystyle a_n }[/math]이 특정한 값 L에 한없이 가까이 다가갈 때, [math]\displaystyle{ \displaystyle (a_n) }[/math]은 L에 수렴한다(converges to L)고 하고,

[math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty}a_n=L }[/math]

로 표기한다. 만약 [math]\displaystyle{ \displaystyle (a_n) }[/math]이 수렴하지 않으면 발산한다(diverges)고 한다.

실해석학에서

실수열 [math]\displaystyle{ \displaystyle (a_n) }[/math]이 주어졌다고 하자. 임의의 실수 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 적당한 [math]\displaystyle{ \displaystyle N\in\mathbb{N} }[/math]이 존재하여 모든 [math]\displaystyle{ \displaystyle n \gt N \left(n\in\mathbb{N}\right) }[/math]에 대해 [math]\displaystyle{ \displaystyle |a_n - L|\lt \varepsilon }[/math]일 때, [math]\displaystyle{ \displaystyle (a_n) }[/math]은 L에 수렴한다고 한다.

예시

[math]\displaystyle{ \displaystyle \frac{1}{n} }[/math]은 n이 커질수록 0으로 한없이 가까이 다가간다.

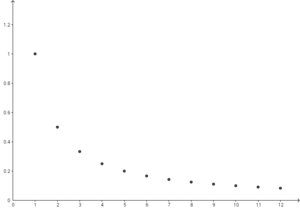
[math]\displaystyle{ \displaystyle a_n=\frac{1}{n} }[/math]인 수열 [math]\displaystyle{ \displaystyle \left\{a_n\right\} }[/math]를 생각하자. 직관적으로 생각하였을 때, [math]\displaystyle{ \displaystyle n }[/math]이 커지면 일반항은 0으로 다가간다는 사실을 알 수 있다. 이제 이를 수열의 극한의 엄밀한 정의를 사용해 증명해보자.

임의의 [math]\displaystyle{ \displaystyle \varepsilon\gt 0 }[/math]에 대해, [math]\displaystyle{ \displaystyle \frac{1}{N}\lt \varepsilon }[/math]를 만족시키는 자연수 [math]\displaystyle{ \displaystyle N }[/math]을 찾을 수 있다. 그럼 [math]\displaystyle{ \displaystyle n\geq N }[/math]일 때, [math]\displaystyle{ \displaystyle \left|a_n-0\right|=\left|\frac{1}{n}\right|\leq\left|\frac{1}{N}\right|=\frac{1}{N}\lt \varepsilon }[/math]이므로, 수열의 극한의 정의에 의해 [math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty}a_n=0 }[/math]이다.

성질

연산

수렴하는 수열 [math]\displaystyle{ \displaystyle (a_n),(b_n) }[/math]에 대해 다음 식이 성립한다.

• [math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty} ca_n = c\lim_{n\to\infty}a_n }[/math]

[math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty}a_n=L }[/math]이라고 하자. 그러면 임의의 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 [math]\displaystyle{ \displaystyle N\in \mathbb{N} }[/math]이 존재하여 임의의 [math]\displaystyle{ \displaystyle n\in \mathbb{N} }[/math]에 대해 [math]\displaystyle{ \displaystyle n\gt N }[/math]이면 [math]\displaystyle{ \displaystyle |a_n-L|\lt \frac{\varepsilon}{|c|+1} }[/math]이다. 그러면

[math]\displaystyle{ \displaystyle |c||a_n-L|=|ca_n-cL|\lt \frac{|c|}{|c|+1}\varepsilon \lt \varepsilon }[/math]

이므로 원하는 결론을 얻는다.

• [math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty} (a_n +b_n)=\lim_{n\to\infty}a_n+\lim_{n\to\infty}b_n }[/math]

[math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty}b_n=M }[/math]이라고 하자. 그러면 임의의 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 [math]\displaystyle{ \displaystyle N_1,N_2\in \mathbb{N} }[/math]가 존재하여 임의의 [math]\displaystyle{ \displaystyle n\in \mathbb{N} }[/math]에 대해 각각 [math]\displaystyle{ \displaystyle n\gt N_1,n\gt N_2 }[/math]이면 [math]\displaystyle{ \displaystyle |a_n-L|\lt \frac{\varepsilon}{2},|b_n-M|\lt \frac{\varepsilon}{2} }[/math]이다. 그러면 임의의 [math]\displaystyle{ \displaystyle \varepsilon\gt 0 }[/math]에 대해 [math]\displaystyle{ \displaystyle \max\{N_1,N_2\} }[/math]가 존재하여 임의의 [math]\displaystyle{ \displaystyle n \gt \max\{N_1,N_2\} }[/math]에 대해 삼각부등식에 의해

[math]\displaystyle{ \displaystyle |(a_n+b_n)-(L+M)|=|(a_n-L)+(b_n-M)|\le|a_n-L|+|b_n-M| \lt \frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon }[/math]

이므로 원하는 결론을 얻는다.

• [math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty} a_nb_n=\left(\lim_{n\to\infty}a_n\right)\left(\lim_{n\to\infty}b_n\right) }[/math]

수렴하는 수열은 항상 유계이다. 즉, 적당한 양의 실수 [math]\displaystyle{ \displaystyle M }[/math]에 대해 [math]\displaystyle{ \displaystyle \left|b_n\right|\leq M,\,\forall n\in\mathbb{N} }[/math]이다. 두 수열 [math]\displaystyle{ \displaystyle \left\{a_n\right\},\left\{b_n\right\} }[/math]의 수렴값을 각각 [math]\displaystyle{ \displaystyle a,b }[/math]라고 하자. 그럼, 임의의 [math]\displaystyle{ \displaystyle \varepsilon\gt 0 }[/math]에 대해 적당한 자연수 [math]\displaystyle{ \displaystyle N_1 }[/math]이 존재하여 [math]\displaystyle{ \displaystyle n\geq N_1 }[/math]이면 [math]\displaystyle{ \displaystyle \left|a_n-a\right|\lt \frac{\varepsilon}{2M} }[/math]이 성립한다. 마찬가지로, 적당한 자연수 [math]\displaystyle{ \displaystyle N_2 }[/math]가 존재하여 [math]\displaystyle{ \displaystyle n\geq N_2 }[/math]이면 [math]\displaystyle{ \displaystyle \left|b_n-b\right|\lt \frac{\varepsilon}{2\left|a\right|+1} }[/math]이 성립한다. [math]\displaystyle{ \displaystyle N=\max\left(N_1,N_2\right) }[/math]라 하자. 그러면, [math]\displaystyle{ \displaystyle n\geq N }[/math]에 대해,

[math]\displaystyle{ \displaystyle \left|a_nb_n-ab\right|=\left|a_nb_n-ab_n+ab_n-ab\right|\leq\left|b_n\right|\left|a_n-a\right|+\left|a\right|\left|b_n-b\right|\lt M\cdot\frac{\varepsilon}{2M}+\left|a\right|\cdot\frac{\varepsilon}{2\left|a\right|+1}\lt \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon }[/math]

이므로 원하는 결론을 얻는다.

• [math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty} \frac{a_n}{b_n}=\frac{\lim_{n\to\infty} a_n}{\lim_{n\to\infty} b_n}\text{ if }\lim_{n\to\infty}b_n\ne 0 }[/math]

[math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty}\frac{1}{a_n}=\frac{1}{\lim_{n\to\infty}a_n}\text{ if }\lim_{n\to\infty}a_n\neq0 }[/math]만 증명하면 된다. 수렴값을 [math]\displaystyle{ \displaystyle a }[/math]라 하자. 그럼, 임의의 [math]\displaystyle{ \displaystyle \varepsilon\gt 0 }[/math]에 대해 적당한 자연수 [math]\displaystyle{ \displaystyle N_1 }[/math]가 존재하여, [math]\displaystyle{ \displaystyle n\geq N_1 }[/math]이면, [math]\displaystyle{ \displaystyle \left|a_n-a\right|\lt \frac{\left|a\right|}{2} }[/math]가 성립한다. 삼각부등식 에 의해, [math]\displaystyle{ \displaystyle \left|\left|a_n\right|-\left|a\right|\right|\lt \frac{\left|a\right|}{2} }[/math]가 성립하고, 좌변의 절댓값을 벗겨주면, [math]\displaystyle{ \displaystyle -\frac{\left|a\right|}{2}\lt \left|a_n\right|-\left|a\right|\lt \frac{\left|a\right|}{2} }[/math]가 성립한다. 여기서 [math]\displaystyle{ \displaystyle \frac{\left|a\right|}{2}\lt \left|a_n\right| }[/math]임을 알 수 있다. 이제, 적당한 자연수 [math]\displaystyle{ \displaystyle N_2 }[/math]에 대해 [math]\displaystyle{ \displaystyle n\geq N_2 }[/math]이면 [math]\displaystyle{ \displaystyle \left|a_n-a\right|\lt \frac{\left|a\right|^2\varepsilon}{2} }[/math]가 성립한다. [math]\displaystyle{ \displaystyle N=\max\left(N_1,N_2\right) }[/math]이라 해주면, [math]\displaystyle{ \displaystyle n\geq N }[/math]일 때,

[math]\displaystyle{ \displaystyle \left|\frac{1}{a_n}-\frac{1}{a}\right|=\frac{\left|a_n-a\right|}{\left|a_n\right|\left|a\right|}\lt \frac{2}{\left|a\right|}\cdot\frac{1}{\left|a\right|}\cdot\frac{\left|a\right|^2\varepsilon}{2}=\varepsilon }[/math]

이 되어 원하는 결론을 얻는다.

유일성

앞에서 [math]\displaystyle{ \displaystyle a_n=\frac{1}{n} }[/math]인 수열 [math]\displaystyle{ \displaystyle (a_n) }[/math]의 극한값이 0임을 보였지만, 다른 극한값이 또 있는 건 아닌지 의심해볼 수 있다. 다행스럽게도 0 말고 다른 극한값은 존재하지 않는다. 일반적으로 실수열의 극한값이 유일함을 보일 수 있다.

[math]\displaystyle{ \displaystyle L_1,L_2 }[/math]를 수열 [math]\displaystyle{ \displaystyle (a_n) }[/math]의 극한값이라고 하자. 그러면 극한의 정의에 의해 임의의 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 [math]\displaystyle{ \displaystyle N\in\mathbb{N} }[/math]이 존재하여 임의의 [math]\displaystyle{ \displaystyle n\in \mathbb{N} }[/math]에 대해 [math]\displaystyle{ \displaystyle n \gt N }[/math]이면 [math]\displaystyle{ \displaystyle |a_n - L_1 | \lt \frac{\varepsilon}{2} }[/math]이고 [math]\displaystyle{ \displaystyle |a_n - L_2|\lt \frac{\varepsilon}{2} }[/math]이다. 그러면 삼각부등식에 의해

[math]\displaystyle{ \displaystyle |L_1 - L_2 | = |(a_n - L_2)-(a_n-L_1)|\le | a_n - L_2|+|a_n-L_1| \lt \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon }[/math]

이다. 이 부등식이 임의의 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 성립하므로 [math]\displaystyle{ \displaystyle L_1=L_2 }[/math]임을 알 수 있다.

확장

복소해석학에서

복소수열 [math]\displaystyle{ \displaystyle (z_n) }[/math]이 주어졌다고 하자. 임의의 실수 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 적당한 [math]\displaystyle{ \displaystyle N\in\mathbb{N} }[/math]이 존재하여 모든 [math]\displaystyle{ \displaystyle n \gt N \left(n\in\mathbb{N}\right) }[/math]에 대해 [math]\displaystyle{ \displaystyle |z_n - L|\lt \varepsilon }[/math]일 때, [math]\displaystyle{ \displaystyle (z_n) }[/math]은 L에 수렴한다고 한다.

거리공간에서

[math]\displaystyle{ \displaystyle (X,d) }[/math]가 거리공간이고 [math]\displaystyle{ \displaystyle (x_n) }[/math]을 X의 점열이라고 하자. 임의의 실수 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 적당한 [math]\displaystyle{ \displaystyle N\in \mathbb{N} }[/math]이 존재하여 모든 [math]\displaystyle{ \displaystyle n \gt N \left(n\in\mathbb{N}\right) }[/math]에 대해 [math]\displaystyle{ \displaystyle d \left( x_n , x \right) \lt \varepsilon }[/math]일 때, [math]\displaystyle{ \displaystyle (x_n) }[/math]은 x에 수렴한다고 한다.

위상공간에서

[math]\displaystyle{ \displaystyle (X,\mathcal{T}) }[/math]가 위상공간이고 [math]\displaystyle{ \displaystyle (x_n) }[/math]은 X의 점열이라고 하자. x를 포함하는 임의의 열린 집합 O에 대해 적당한 [math]\displaystyle{ \displaystyle N\in\mathbb{N} }[/math]이 존재하여 모든 [math]\displaystyle{ \displaystyle n \gt N \left(n\in\mathbb{N}\right) }[/math]에 대해 [math]\displaystyle{ \displaystyle x_n \in O }[/math]일 때, [math]\displaystyle{ \displaystyle (x_n) }[/math]은 x에 수렴한다고 한다.

일반적으로 위상공간에선 점열의 극한이 유일하지 않다.

[math]\displaystyle{ \displaystyle \mathbb{R} }[/math] 위의 유한여집합위상을 [math]\displaystyle{ \displaystyle \mathcal{T} }[/math]라고 하자. 이때 위상공간 [math]\displaystyle{ \displaystyle (\mathbb{R},\mathcal{T}) }[/math]에서 정의된 서로 다른 점들의 점열을 [math]\displaystyle{ \displaystyle (x_n) }[/math]이라고 하자. [math]\displaystyle{ \displaystyle x\in \mathbb{R} }[/math]를 포함하는 임의의 열린 집합 [math]\displaystyle{ \displaystyle O }[/math]에 대해 [math]\displaystyle{ \displaystyle \mathbb{X}\setminus O }[/math]는 위상의 정의에 의해 유한집합이다. 즉 [math]\displaystyle{ \displaystyle x_n \not\in O }[/math]인 원소는 많아봐야 유한 개이므로 [math]\displaystyle{ \displaystyle x_N\not\in O }[/math]인 가장 큰 [math]\displaystyle{ \displaystyle N\in \mathbb{N} }[/math]이 존재한다. 즉, 임의의 자연수 [math]\displaystyle{ \displaystyle n\gt N }[/math]에 대해 [math]\displaystyle{ \displaystyle x_n\in O }[/math]이므로 [math]\displaystyle{ \displaystyle (x_n) }[/math]은 [math]\displaystyle{ \displaystyle x }[/math]에 수렴한다. [math]\displaystyle{ \displaystyle x }[/math]가 임의의 실수이므로, [math]\displaystyle{ \displaystyle (x_n) }[/math]은 임의의 실수에 수렴한다.

하우스도르프 공간에서 수렴하는 점열의 극한값은 유일하다.