피타고라스 정리: 두 판 사이의 차이

2015년 8월 21일 (금) 03:01 판

개요

고대 그리스의 수학자인 피타고라스의 이름을 따서 지은 정리인 피타고라스 정리(Pythagorean theorem, Pythagoras' theorem)는 유클리드 공간에서 직각삼각형에서 성립하는 식을 담고 있다. 빗변의 길이를 [math]\displaystyle{ c }[/math]라고 하고, 다른 두 변의 길이를 [math]\displaystyle{ a,b }[/math]라고 했을 때,

[math]\displaystyle{ \displaystyle{a^2 + b^2 = c^2} }[/math]

이 성립한다.

이 정리는 피타고라스가 활동하던 고대 그리스 시대 이전부터 잘 알려져 있었다. 한 기록에는 피타고라스가 발견하기 한참 전에 고대 중국에서 이 정리를 알고 있었다는 내용도 있다. 다만, 피타고라스의 이름을 따 지은 것은 피타고라스가 정리를 처음으로 증명했기 때문이다.

증명

매우 간단한 식인 만큼, 증명도 수백가지가 넘는다. 여기에 그 많은 방법을 다 적을 순 없으니 대표적인 몇 가지만 기술한다.

피타고라스

피타고라스의 방법은 두 가지가 있다.

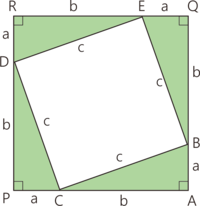
그림에서 [math]\displaystyle{ \triangle ABC \equiv \triangle BEQ \equiv \triangle DER \equiv \triangle CDP }[/math]이고 [math]\displaystyle{ \Box BCDE }[/math]는 정사각형이다. 따라서 [math]\displaystyle{ \Box APRQ = 4 \triangle ABC + \Box BCDE }[/math]이고 이를 [math]\displaystyle{ a, b, c }[/math]로 나타내면 [math]\displaystyle{ (a+b)^2=c^2+4\times{ab \over 2} }[/math]. 괄호를 풀고 분수를 정리하면 [math]\displaystyle{ a^2+2ab+b^2=c^2+2ab }[/math], 양변에서 [math]\displaystyle{ 2ab }[/math]를 빼면 [math]\displaystyle{ a^2+b^2=c^2 }[/math], 피타고라스의 정리가 된다.

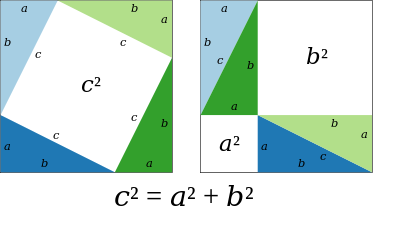
직각삼각형의 배열을 이용하는 방법도 있다. 양 그림에서 흰색 부분에 해당하는 넓이는 같다. 이 흰색 부분에 해당하는 넓이는 다른 직각삼각형 네 개를 어떻게 배열하냐에 따라 다르게 표현할 수 있는데, 왼쪽에서는 [math]\displaystyle{ c^2 }[/math], 오른쪽에서는 [math]\displaystyle{ a^2+b^2 }[/math]이다. 따라서 [math]\displaystyle{ a^2+b^2=c^2 }[/math]

유클리드

파일:피타고라스 정리 2.png

각 변의 제곱은 그 변의 길이를 한 변으로 하는 정사각형으로 나타낼 수 있다. 위 그림에서, [math]\displaystyle{ S_{\triangle{AFB}}=S_{\triangle{FCB}}=S_{\triangle{ABD}}=S_{\triangle{BKD}} }[/math]이고, 같은 방법으로 [math]\displaystyle{ S_{\triangle{ACI}}=S_{\triangle{CKE}} }[/math]를 보일 수 있다 (평행한 두 선 사이의 밑변의 길이가 같은 삼각형은 넓이가 모두 같다는 사실을 이용한다). 이걸 식으로 나타내면 [math]\displaystyle{ \frac{1}{2}a^2+\frac{1}{2}b^2=\frac{1}{2}c^2 }[/math]이고, 따라서 [math]\displaystyle{ a^2+b^2=c^2 }[/math]이다.

참고로 이 방법은 대부분의 교과서에도 나와있는 대표적인 방법.

바스카라

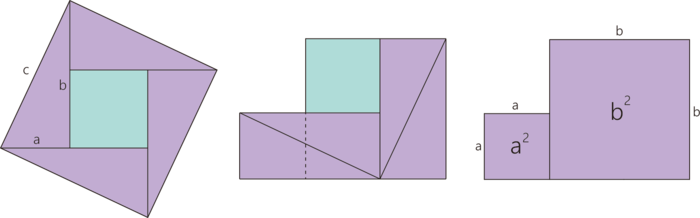
직관적으로 알 수 있는 가장 쉬운 방법이다. 첫 번째 그림은 밑변이 [math]\displaystyle{ a }[/math], 높이가 [math]\displaystyle{ b }[/math]인 직각삼각형 4개와 한 변의 길이가 [math]\displaystyle{ b-a }[/math]인 정사각형으로 구성된 한 변이 [math]\displaystyle{ c }[/math]이고 넓이가 [math]\displaystyle{ c^2 }[/math]인 정사각형이다. 그리고 직각삼각형을 재배치하면 두 번째 그림처럼 되는데 이는 세 번째 그림에서 알 수 있듯이 넓이가 [math]\displaystyle{ a^2 }[/math]인 정사각형과 넓이가 [math]\displaystyle{ b^2 }[/math]인 정사각형 두 개인 것을 알 수 있다. 앞서 재배치하기 전의 정사각형이 [math]\displaystyle{ c^2 }[/math]이고 이를 재배치한 것이 [math]\displaystyle{ a^2+b^2 }[/math]이니 [math]\displaystyle{ c^2=a^2+b^2 }[/math]이다.

가필드

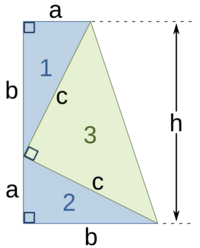
위 사다리꼴의 넓이는 [math]\displaystyle{ \frac{1}{2}\left(a+b\right)\left(a+b\right)=\frac{a^2+b^2+2ab}{2} }[/math]이다. 한편, 넓이를 세 직각삼각형의 넓이의 합으로도 나타낼 수 있는데, 이 경우 [math]\displaystyle{ 2\cdot\frac{1}{2}ab+\frac{1}{2}c^2=ab+\frac{c^2}{2} }[/math]이다. 곧, [math]\displaystyle{ \frac{a^2+b^2+2ab}{2}=ab+\frac{c^2}{2} }[/math]이고, 정리하면 [math]\displaystyle{ a^2+b^2=c^2 }[/math]이다.

피타고라스 수

자연수 중에서 피타고라스 정리를 만족하는 세 수를 피타고라스 수라고 한다. 즉, 직각삼각형을 만드는 자연수 길이의 세 쌍이다. 가장 작은 피타고라스 수는 [math]\displaystyle{ (3,4,5) }[/math]이다. 세 수는 다음과 같이 3개의 자연수로 유일하게 나타낼 수 있다.

[math]\displaystyle{ a = k \cdot (m^2 - n^2) , b = k \cdot (2mn) , c = k \cdot (m^2 + n^2) }[/math]

단, [math]\displaystyle{ n \lt m }[/math]이고, [math]\displaystyle{ m-n }[/math]가 홀수이며, [math]\displaystyle{ m,n }[/math]은 서로소이다.

다음은 몇 가지 피타고라스 수를 나열한 것이다.

[math]\displaystyle{ (3, 4, 5), (11, 60, 61), (16, 63, 65) }[/math]

[math]\displaystyle{ (33, 56, 65), (5, 12, 13), (13, 84, 85) }[/math]

[math]\displaystyle{ (20, 21, 29), (39, 80, 89), (7, 24, 25) }[/math]

[math]\displaystyle{ (8, 15, 17), (28, 45, 53), (48, 55, 73) }[/math]

[math]\displaystyle{ (9, 40, 41), (12, 35, 37), (36, 77, 85), (65, 72, 97) }[/math]

이외에도 [math]\displaystyle{ (6, 8, 10), (9, 12, 15) }[/math]와 같이 피타고라스 수에 자연수를 곱해도 피타고라스 수이고, 원래 삼각형과 닮음이다.

여담

피타고라스 학파는 유리수만이 수의 전부라고 믿었다. 그런데, 피타고리스 학파의 한 학자인 히파수스가 짧은 두 변이 1이면 빗변의 길이가 [math]\displaystyle{ \sqrt{2} }[/math]인데, 이 수는 유리수가 아니다는 사실을 알아챘고, 피타고라스 학파는 혼란에 빠졋다. 이후 이 말을 들은 피타고라스는 자신이 믿고 있는 이치에 맞지 않다고 여겨 히파수스를 죽였다느니, 히파수스가 세상에 무리수의 존재를 알리려다가 암살당했다느니 하는 이야기가 있는 반면, 히파수스가 피타고라스 학파의 신념을 지키기 위해 자살했다는 얘기도 있다. ~~아 몰랑! 유리수 빼곤 다 수가 아니야!~~ 하지만 어느쪽이든 진실은 불명이며, 심지어는 히파수스가 무리수를 발견했다는 사실이 맞는지도 의문에 싸여있다.

중학교 수학에서는 그 중요성으로 인해 아예 단원 하나를 차지하고 있다.

@@ 17번째 줄: / 17번째 줄: @@
 그림에서 <math>\triangle ABC \equiv \triangle BEQ \equiv \triangle DER \equiv \triangle CDP</math>이고 <math>\Box BCDE</math>는 정사각형이다. 따라서 <math>\Box APRQ = 4 \triangle ABC + \Box BCDE</math>이고 이를 <math>a, b, c</math>로 나타내면 <math>(a+b)^2=c^2+4\times{ab \over 2}</math>. 괄호를 풀고 분수를 정리하면 <math>a^2+2ab+b^2=c^2+2ab</math>, 양변에서 <math>2ab</math>를 빼면 <math>a^2+b^2=c^2</math>, 피타고라스의 정리가 된다.
-[[파일:피타고라스 정리 1.png|가운데|400픽셀]]
+[[파일:Pythagoras-proof-anim.svg|가운데|400픽셀]]
 직각삼각형의 배열을 이용하는 방법도 있다. 양 그림에서 흰색 부분에 해당하는 넓이는 같다. 이 흰색 부분에 해당하는 넓이는 다른 [[직각삼각형]] 네 개를 어떻게 배열하냐에 따라 다르게 표현할 수 있는데, 왼쪽에서는 <math>c^2</math>, 오른쪽에서는 <math>a^2+b^2</math>이다. 따라서 <math>a^2+b^2=c^2</math>