평행사변형

파일:평행사변형.png

Parallelogram

정의

사각형 중, 두 쌍의 대변이 각각 평행한 사각형. 사다리꼴의 세부 분류이며, 사다리꼴과는 달리 학교에서 자세히 다루게 되는 도형이다.

필요충분조건

일단 평행사변형의 정의는 따로 있지만, 그 정의와 필요충분조건인 다른 조건들이 꽤 많다. 아래는 그 목록.

1. 두 쌍의 대변의 길이가 같다.
2. 두 쌍의 대각의 크기가 같다.
3. 두 대각선이 서로를 이등분한다.
4. 한 쌍의 대변이 평행하고, 그 길이가 같다.

증명

1. [math]\displaystyle{ \triangle{ABC}\cong\triangle{CDA} }[/math](SSS 합동)임을 쉽게 알 수 있다. 따라서 [math]\displaystyle{ \angle{CAB}=\angle{ACD} }[/math]이고, 이는 곧 [math]\displaystyle{ \overline{AB}\parallel\overline{CD} }[/math]를 의미한다 (엇각). 마찬가지로 [math]\displaystyle{ \triangle{ADB}\cong\triangle{CBD} }[/math](SSS 합동)이고, [math]\displaystyle{ \angle{ADB}=\angle{CBD} }[/math]이므로 [math]\displaystyle{ \overline{AD}\parallel\overline{BC} }[/math]이다 (엇각).

2. [math]\displaystyle{ \angle{A}=\angle{C}=\alpha,\,\angle{B}=\angle{D}=\beta }[/math]라 하자. 사각형의 내각의 합은 360도 이므로, [math]\displaystyle{ 2\alpha+2\beta=360^\circ,\,\alpha+\beta=180^\circ }[/math]이다. 이를 이용해 엇각을 보일 수 있고, 따라서 [math]\displaystyle{ \overline{AB}\parallel\overline{CD},\,\overline{AD}\parallel\overline{BC} }[/math]이다.

3. [math]\displaystyle{ \triangle{AEB}\cong\triangle{CED} }[/math](SAS 합동)이고, 따라서 [math]\displaystyle{ \angle{EAB}=\angle{ECD} }[/math]이므로 [math]\displaystyle{ \overline{AB}\parallel\overline{CD} }[/math]이다 (엇각). 마찬가지로 [math]\displaystyle{ \triangle{AED}\cong\triangle{CEB} }[/math]이고, 따라서 [math]\displaystyle{ \angle{EAD}=\angle{ECB} }[/math]이므로 [math]\displaystyle{ \overline{AD}\parallel\overline{BC} }[/math]이다 (엇각).

4. [math]\displaystyle{ \overline{AB}\parallel\overline{CD} }[/math]이므로 [math]\displaystyle{ \angle{EAB}=\angle{ECD},\,\angle{EBA}=\angle{EDC} }[/math]이다 (엇각). 따라서 [math]\displaystyle{ \triangle{EAB}\cong\triangle{ECD} }[/math](ASA 합동)이고, 3번 조건에 의해 증명하고자 하는 바가 증명되었다.

역의 증명

1. [math]\displaystyle{ \overline{AB}\parallel\overline{CD} }[/math]이므로 [math]\displaystyle{ \angle{CAB}=\angle{ACD} }[/math]. 또한, [math]\displaystyle{ \overline{AD}\parallel\overline{BC} }[/math]이므로 [math]\displaystyle{ \angle{ACB}\angle{CAD} }[/math]. 그리고 [math]\displaystyle{ \overline{AC} }[/math]공통. 따라서 [math]\displaystyle{ \triangle{ABC}\cong\triangle{CDA} }[/math](ASA 합동). 따라서 [math]\displaystyle{ \overline{AB}=\overline{CD},\,\overline{AD}=\overline{BC} }[/math].

2. [math]\displaystyle{ \overline{AB}\parallel\overline{CD} }[/math]이므로 [math]\displaystyle{ \angle{CAB}=\angle{ACD} }[/math]. [math]\displaystyle{ \overline{AD}\parallel\overline{BC} }[/math]이므로 [math]\displaystyle{ \angle{DAC}=\angle{BCA} }[/math]. 따라서 [math]\displaystyle{ \angle A=\angle C }[/math]. 마찬가지 방법으로 [math]\displaystyle{ \angle B=\angle D }[/math]를 증명할 수 있다.

3. 1번에 의해 [math]\displaystyle{ \overline{AB}=\overline{CD} }[/math]. 또한, [math]\displaystyle{ \overline{AB}\parallel\overline{CD} }[/math]이므로 [math]\displaystyle{ \angle{EAB}=\angle{ECD},\,\angle{EBA}=\angle{EDC} }[/math]. 따라서 [math]\displaystyle{ \triangle{EAB}\cong\triangle{ECD} }[/math] (ASA 합동). 그러므로 [math]\displaystyle{ \overline{EA}=\overline{EC},\,\overline{EB}=\overline{ED} }[/math]

4. 1번에 의해 증명이 완료되었다.

넓이

사다리꼴의 넓이는 직사각형과 마찬가지로 밑변[math]\displaystyle{ \times }[/math]높이인데, 이유는 간단하다. 튀어나온 부분을 툭 짤라서 반대편에 붙이면 직사각형이 되기 때문. 혹은 [math]\displaystyle{ \overline{AB}=a,\,\overline{BC}=b,\,\angle{A}=\theta }[/math]라 하면 삼각함수를 이용해 [math]\displaystyle{ 2\times\frac{1}{2}\times ab\sin\theta=ab\sin\theta }[/math]로 구할 수도 있다. 대각선의 길이를 이용할 수도 있는데, 두 대각선의 길이를 각각 [math]\displaystyle{ p,q }[/math]라 하고 교각을 [math]\displaystyle{ \theta }[/math]라 하면 [math]\displaystyle{ \frac{1}{2}pq\sin\theta }[/math]가 넓이가 된다. 이유는 두 대각선을 변으로 하는 평행사변형을 만들었을 때, 원 사각형의 넓이의 두배가 되기 때문.

응용

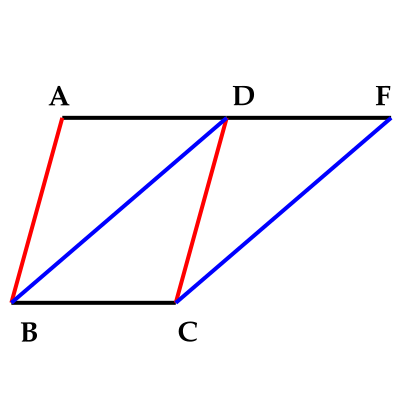
유클리드 기하학 원론 제1권 법칙35

Parallelograms on the same base (BC) and between the same parallels are equal.

같은 밑변(BC)과 같은 평행선 사이의 평행사변형들(parallelograms)은 같습니다.(유클리드 기하학 원론 제1권 법칙35)

이러한 제1권35번 법칙(theorem)은 평행사변형의 정의 및 성질을 잘 보여줄뿐만아니라 평행사변형들의 변형된 모습에서 일관된 크기를 유지한다는 사실을 증명해보여줌으로써 유클리드 기하학적인 피타고라스 정리(유클리드 기하학 원론 제1권 법칙47)를 증명해 보여준다.

관련 항목

• 사각형
• 사다리꼴
• 마름모
• 직사각형
• 정사각형

---

• [참고](유클리드 기하학 원론,구텐베르크 프로젝트,John Casey 1885)http://www.gutenberg.org/files/21076/21076-pdf.pdf?session_id=9bfd9ef535a37ac859a6028f101fa4451e3226cc