잔글편집 요약 없음 |
(→관련 항목) |
||
| (사용자 2명의 중간 판 2개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
Chord | Chord | ||
| 41번째 줄: | 41번째 줄: | ||
*[[원주각]] | *[[원주각]] | ||
*[[호 (수학)]] | *[[호 (수학)]] | ||
*[[활꼴]] | |||
*[[변심거리]] | |||
[[분류:기하학]] | [[분류:기하학]] | ||
2022년 3월 11일 (금) 18:27 기준 최신판
Chord
정의[편집 | 원본 편집]
할선의 부분집합으로, 원에 포함되는 부분을 (원주 위의 두 점 포함) 현이라 한다. 좀 더 일반화시켜 정의하면 어떤 곡선 위의 두 점을 이은 선분이라 할 수 있다.
성질[편집 | 원본 편집]
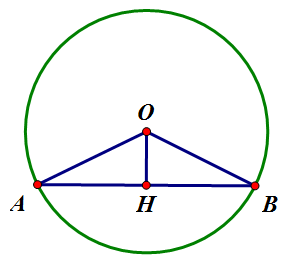
1. 원의 중심에서 현에 수선을 내리면 현을 이등분한다. 역으로 현에 중선을 내리면 그 중선은 수선이다.
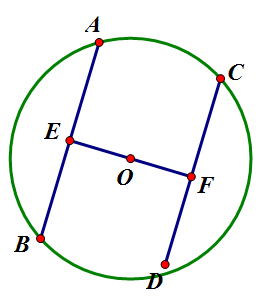
2. 원의 중심에서 같은 거리에 있는 두 현은 길이가 같다.
3. 한 원, 혹은 합동인 두 원에서 중심각의 크기가 같은 두 현은 길이가 같다.
4. 한 원, 혹은 합동인 두 원에서 두 현의 길이가 같으면 중심각의 크기도 같다.
5. 현의 길이와 호의 길이는 비례하지 않는다. 정확히 말하면, 현의 길이가 늘어나면 호의 길이도 늘어나나 단순 비례는 아니다.
6. 가장 긴 현은 원의 지름.
증명[편집 | 원본 편집]
1. 원의 중심 [math]\displaystyle{ O }[/math]에서 현 [math]\displaystyle{ \overline{AB} }[/math]에 내린 수선을 [math]\displaystyle{ H }[/math]라 하자. 그럼 [math]\displaystyle{ \overline{OA}=\overline{OB} }[/math] (반지름), [math]\displaystyle{ \angle{OHA}=\angle{OHB}=\angle{R} }[/math], [math]\displaystyle{ \overline{OH} }[/math]공통이므로 [math]\displaystyle{ \triangle{OAH}\cong\triangle{OBH} }[/math] (RHS 합동). [math]\displaystyle{ \therefore\overline{HA}=\overline{HB} }[/math]
이제 원의 중심 [math]\displaystyle{ O }[/math]에서 현 [math]\displaystyle{ \overline{AB} }[/math]에 내린 중선을 [math]\displaystyle{ H }[/math]라 하자. 그럼 [math]\displaystyle{ \overline{OA}=\overline{OB} }[/math] (반지름), [math]\displaystyle{ \overline{HA}=\overline{HB} }[/math], [math]\displaystyle{ \overline{OH} }[/math]공통이므로 [math]\displaystyle{ \triangle{OAH}\cong\triangle{OBH} }[/math] (SSS 합동). [math]\displaystyle{ \therefore\angle{OHA}=\angle{OHB} }[/math]
2, 3, 4. 원의 중심 [math]\displaystyle{ O }[/math]에서 두 현 [math]\displaystyle{ \overline{AB},\overline{CD} }[/math]에 내린 수선의 발을 각각 [math]\displaystyle{ E, F }[/math]라 하자. 그럼 1번 성질에 의해 [math]\displaystyle{ \overline{AE}=\overline{CF} }[/math]만 증명하면 된다. 먼저 [math]\displaystyle{ \overline{OE}=\overline{OF} }[/math]라 가정하자. 그럼 [math]\displaystyle{ \overline{OA}=\overline{OC} }[/math] (반지름), [math]\displaystyle{ \angle{OEA}=\angle{OFC}=\angle{R} }[/math]이므로 [math]\displaystyle{ \triangle{OEA}\cong\triangle{OFC} }[/math] (RHA 합동)이다. 따라서 [math]\displaystyle{ \overline{AE}=\overline{CF} }[/math].
이제 [math]\displaystyle{ \angle{AOB}=\angle{COD} }[/math]라 가정하자. 그럼 [math]\displaystyle{ \overline{OA}=\overline{OB}=\overline{OC}=\overline{OD} }[/math] (반지름) 이므로 [math]\displaystyle{ \triangle{OAB}\cong\triangle{OCD} }[/math] (SAS 합동)이다. 따라서 따라서 [math]\displaystyle{ \overline{AB}=\overline{CD} }[/math].
마지막으로 [math]\displaystyle{ \overline{AB}=\overline{CD} }[/math]라 가정하자. [math]\displaystyle{ \overline{OA}=\overline{OB}=\overline{OC}=\overline{OD} }[/math] (반지름) 이므로 [math]\displaystyle{ \triangle{OAB}\cong\triangle{OCD} }[/math] (SSS 합동)이다. 따라서 [math]\displaystyle{ \angle{AOB}=\angle{COD} }[/math].
5. 중심각을 [math]\displaystyle{ \theta }[/math], 반지름을 1이라 하면, 호의 길이는 [math]\displaystyle{ \theta }[/math] (라디안) 이고, 현의 길이는 코사인 법칙에 의해 [math]\displaystyle{ \sqrt{2-2\cos\theta} }[/math]이다. 딱봐도 절대 비례하지 않는다.
6. 지름보다 긴 현이 있다고 가정하자. 일단 그 현은 지름이 될 수 없고, 따라서 원의 중심 [math]\displaystyle{ O }[/math]에서 현 [math]\displaystyle{ \overline{AB} }[/math]에 수선의 발을 내릴 수 있다. 수선의 발을 [math]\displaystyle{ H }[/math]라 하자. 1번 성질에 의해 현은 이등분되며, 이등분된 현은 원의 반지름보다 길어야 한다. 그런데 직각삼각형 [math]\displaystyle{ \triangle{OAH} }[/math]에서 빗변이 반지름인데, 밑변이 빗변보다 기므로 모순이다 (사인 법칙 참조). 따라서 지름보다 긴 현은 없다.