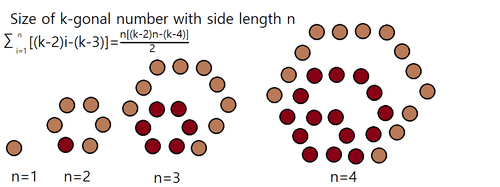
다각수(多角數, polygonal number)란 정다각형을 만드는 숫자를 말한다. 예를 들면 변의 길이가 n개인 정삼각형을 만드는 수는 삼각수, 변의 길이가 n개인 정사각형을 만드는 숫자는 사각수(=제곱수) 이런 식으로 한다.
다각수를 만들 때에는 한 꼭짓점은 공통으로 하고 다른 꼭짓점과 변을 덧붙여 나가서 만든다. 페르마의 다각수 정리에 따라 임의의 자연수는 많아야 n개의 n각수의 합으로 표현 가능하다.
다각수의 공식
변의 길이가 n개인 k각수의 크기는 다음과 같이 구해진다.
우선 n=1일 때는 k값과는 무관하게 1이 되며, 변의 길이가 n → n+1이 될 때마다 (k-2)n+(k-3)개가 추가된다. 따라서 변의 길이가 n인 k각수의 공식은 다음과 같이 주어진다.
- [math]\displaystyle{ P(k, n) = \sum_{i=1}^{n} {[(k-2)i+(k-3) ]} = \frac{n[(k-2)n-(k-4)]}{2} = (k-2)\frac{n(n-1)}{2}+n }[/math]
또한 n번째 k각수는 n번째 삼각수 Tn에 대해 다음과 같은 관계식을 가진다.[1]
- [math]\displaystyle{ P(k,n) = (k-2)T_{n-1} + n = (k-3)T_{n-1} + T_n\, }[/math]
또한 다음과 같은 관계식도 성립한다.
- [math]\displaystyle{ P(k,n+1)-P(k,n) = (k-2)n + 1\, , }[/math]
- [math]\displaystyle{ P(k+1,n) - P(k,n) = T_{n-1} = \frac{n(n-1)}{2}\, }[/math]
k각수 P(k,n) 가 x일 때, 우리는 n 값을 다음과 같이 구할 수 있다.
- [math]\displaystyle{ n = \frac{\sqrt{8(k-2)x+(k-4)^2}+(k-4)}{2(k-2)} }[/math]
다각수의 종류
삼각수
이와 관련한 주제는 삼각수에서 다룹니다.영어로는 Triangular Number이라고 부른다.
사각수
이와 관련한 주제는 제곱수에서 다룹니다.영어로는 Square (Number)이라고 부른다.
오각수
오각수(五角數, Pentagonal Number)는 정오각형을 이루는 숫자를 말한다.
처음 열 개의 항은 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, ...처럼 나가며, 더 많은 항은 oeis:A000326에서 확인할 수 있다. 수열의 공식은 [math]\displaystyle{ \frac{n(3n-1)}{2} }[/math]이다.
오각수에서 n의 값이 0 미만의 정수를 집어넣을 때 나타나는 수를 일반화된 오각수(Generalized pentagonal number)이라고 부른다. n이 양의 자연수일 때는 [math]\displaystyle{ \frac{n(3n\pm 1)}{2} }[/math]
이것과 관련된 정리로 오일러의 오각수 정리(Euler's Pentagonal Number Theorem)이 있는데 이것은 조합론적으로 n 분할(Partition)에 대해 분할된 집합의 원수 수가 모든 분할의 갯수가 다른 짝수개 분할에서(disjoint even partition)에서 모든 분할의 원소 갯수가 다른 홀수개 분할(disjoint odd partition)의 차이가 ±1이 되는 시점이 n이 일반화된 오각수라는 것을 의미하는 것이다. 다시 말해 아래와 같은 공식이 성립한다는 것을 말한다.
[math]\displaystyle{ \prod_{i=1}^{\infty} (1- x^i ) = \sum_{i=\infty}^{\infty} { {(-1)}^i x^{{i(3i-1)}/{2}}} }[/math]
육각수
육각수(六角數, Hexagonal Number)는 정육각형을 이루는 숫자를 말한다.
처음 열 개의 항은 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, ...처럼 나가며, 더 많은 항은 oeis:A000384에서 확인할 수 있다. 육각수의 공식은 [math]\displaystyle{ n(2n-1) }[/math]로 나타낼 수 있으며, 이는 2n-1번째 삼각수 [math]\displaystyle{ T_{2n-1} = \frac{(2n-1)2n}{2} }[/math]와 동일하다.
관련 문서
각주
- ↑ 영어 위키페디아 문서 wikipedia:Polygonal number 인용
