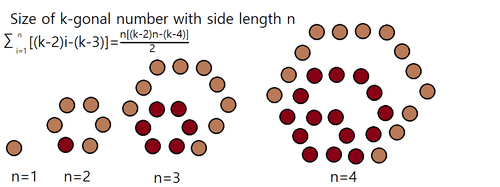
다각수(多角數, polygonal number)란 정다각형을 만드는 숫자를 말한다. 예를 들면 변의 길이가 n개인 정삼각형을 만드는 수는 삼각수, 변의 길이가 n개인 정사각형을 만드는 숫자는 사각수(=제곱수) 이런 식으로 한다.
다각수를 만들 때에는 한 꼭짓점은 공통으로 하고 다른 꼭짓점과 변을 덧붙여 나가서 만든다. 페르마의 다각수 정리에 따라 임의의 자연수는 많아야 n개의 n각수의 합으로 표현 가능하다.
다각수의 공식[편집 | 원본 편집]
변의 길이가 n개인 k각수의 크기는 다음과 같이 구해진다.
우선 n=1일 때는 k값과는 무관하게 1이 되며, 변의 길이가 n → n+1이 될 때마다 (k-2)n+(k-3)개가 추가된다. 따라서 변의 길이가 n인 k각수의 공식은 다음과 같이 주어진다.
- [math]\displaystyle{ P(k, n) = \sum_{i=1}^{n} {[(k-2)i+(k-3) ]} = \frac{n[(k-2)n-(k-4)]}{2} = (k-2)\frac{n(n-1)}{2}+n }[/math]
또한 n번째 k각수는 n번째 삼각수 Tn에 대해 다음과 같은 관계식을 가진다.[1]
- [math]\displaystyle{ P(k,n) = (k-2)T_{n-1} + n = (k-3)T_{n-1} + T_n\, }[/math]
또한 다음과 같은 관계식도 성립한다.
- [math]\displaystyle{ P(k,n+1)-P(k,n) = (k-2)n + 1\, , }[/math]
- [math]\displaystyle{ P(k+1,n) - P(k,n) = T_{n-1} = \frac{n(n-1)}{2}\, }[/math]
k각수 P(k,n) 가 x일 때, 우리는 n 값을 다음과 같이 구할 수 있다.
- [math]\displaystyle{ n = \frac{\sqrt{8(k-2)x+(k-4)^2}+(k-4)}{2(k-2)} }[/math]
다각수의 종류[편집 | 원본 편집]
삼각수[편집 | 원본 편집]
영어로는 Triangular Number이라고 부른다.
사각수[편집 | 원본 편집]
영어로는 Square (Number)이라고 부른다.
오각수[편집 | 원본 편집]
오각수(五角數, Pentagonal Number)는 정오각형을 이루는 숫자를 말한다.
처음 열 개의 항은 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, ...처럼 나가며, 더 많은 항은 oeis:A000326에서 확인할 수 있다. 수열의 공식은 [math]\displaystyle{ \frac{n(3n-1)}{2} }[/math]이다.
오각수에서 n의 값이 0 미만의 정수를 집어넣을 때 나타나는 수를 일반화된 오각수(Generalized pentagonal number)이라고 부른다. n이 양의 자연수일 때는 [math]\displaystyle{ \frac{n(3n\pm 1)}{2} }[/math]
이것과 관련된 정리로 오일러의 오각수 정리(Euler's Pentagonal Number Theorem)이 있는데 이것은 조합론적으로 n 분할(Partition)에 대해 분할된 집합의 원수 수가 모든 분할의 갯수가 다른 짝수개 분할에서(disjoint even partition)에서 모든 분할의 원소 갯수가 다른 홀수개 분할(disjoint odd partition)의 차이가 ±1이 되는 시점이 n이 일반화된 오각수라는 것을 의미하는 것이다. 다시 말해 아래와 같은 공식이 성립한다는 것을 말한다.
[math]\displaystyle{ \prod_{i=1}^{\infty} (1- x^i ) = \sum_{i=\infty}^{\infty} { {(-1)}^i x^{{i(3i-1)}/{2}}} }[/math]
육각수[편집 | 원본 편집]
육각수(六角數, Hexagonal Number)는 정육각형을 이루는 숫자를 말한다.
처음 열 개의 항은 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, ...처럼 나가며, 더 많은 항은 oeis:A000384에서 확인할 수 있다. 육각수의 공식은 [math]\displaystyle{ n(2n-1) }[/math]로 나타낼 수 있으며, 이는 2n-1번째 삼각수 [math]\displaystyle{ T_{2n-1} = \frac{(2n-1)2n}{2} }[/math]와 동일하다.
관련 문서[편집 | 원본 편집]
각주
- ↑ 영어 위키페디아 문서 wikipedia:Polygonal number 인용
| 수의 종류 | |
|---|---|
| 수학 상수 | |
| 자연수 및 정수 | |
| 유리수 및 실수 | |
| 복소수 및 확장 | |