구구단

걸그룹에 관한 내용은 구구단 (아이돌) 문서를 읽어 주세요.

영어: Multiplication table / 일본어: 九九(くく) / 중국어: 乘法表

구구단

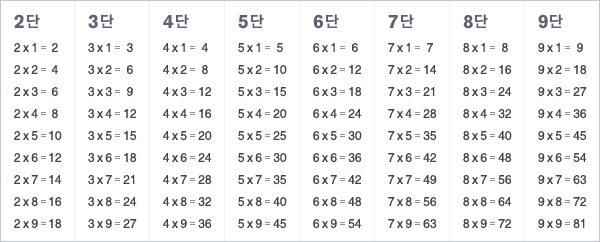
2×2부터 9×9까지를 다루는 일종의 표로, 공식적으로는 초등학교에서 곱셈을 익히는 단계에 암기 교육을 진행한다. 십진법 체계상에서 필요한 기초적인 한 자릿수 간의 곱셈을 나열한 것으로, 일일히 덧셈 등을 이용해 계산하지 않고 곧바로 곱셈 도구를 사용할 수 있게 해주기 위해 배운다.

불필요한 계산의 반복과정을 생략해 빠르게 곱셈의 결과를 도출해낼 수 있다는 점에서, 산수(算數)를 배우는데 필수적인 요소다. 원리적으론 1×1부터 10×10까지(The Decimal Multiple Table)를 범위로 하지만, 이 둘은 숫자만 셀 줄 안다면 굳이 기억할 필요조차 없기에 생략하곤 한다.

예를 들어, 구구단을 외우지 않았을 경우에는 8×8을 정의대로 8을 8번 더하는 과정을 거쳐야 하지만, 그 결과를 정리해놓은 구구단을 외웠을 경우에는 바로 64라는 답을 얻을 수 있다.

십구단

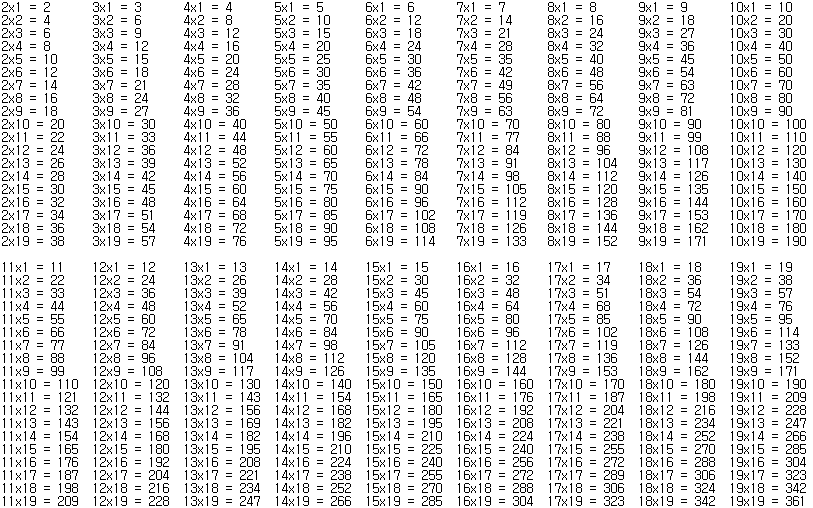
수학 실력이 뛰어난 인도의 학생들이 외운다고 하여 옛날에 유행했던 십구단 또는 십구구단이다. 말 그대로 19×19까지 다룬다.

하지만 이걸 외운다고 해서 수학적 사고능력이 늘어나는 것은 아니다. 기초연산에 필요한 곱셈은 구구단으로도 충분하며, 저런 단순계산은 그저 계산기를 사용하지 못하게 강제하는 상황에서나 약간 도움이 될 뿐, 수학적 사고능력과는 아무 상관이 없다. 그나마 계산기가 없어도 구구단과 곱셈법칙만 알고 있다면 종이에 간단하게 계산해낼 수 있다. 그나마 도움이 될 가능성이 있는 경우는 딱 하나인데, 좀 큰 수의 소인수분해를 할 경우 약간의 속도가 빨라지는 효과는 있을 수 있다. 물론 종이로 해결 가능한 것과 아주 빠른 속도차이가 나는 경우는 드물다.

비슷한 이유로 11단이나 12단 등도 우월감을 위해 외우려 하기도 하지만, 기억력 향상이라면 모를까, 노력에 비해 실제 수학실력이나 활용력 증진에 효과적이다라고 보기는 좀 어렵다.

이야기거리

• 제곱수(n², Square Number)를 외우는 것도 구구단 외우기와 비슷한 이유이다. 제곱수는 대체로 1²부터 15²(225)까지, 혹은 19²(361)까지 외운다. 단, 구구단과는 달리 필수 교육과정은 아니다.
• 반대로 2의 거듭제곱(2ⁿ, Power of Two)을 외우는 것도 동일하다. 대개 2의 0제곱(1)부터 2의 10제곱(1024)까지 외운다.