페르마 점

Fermat point

개요

삼각형이 하나 있다고 가정하자. 이 삼각형 안의 무수히 많은 점들 중에서, 세 꼭짓점까지의 거리의 합이 가장 작게되는 점을 찾고 싶다고 하자. 그럼, 대부분의 사람들은 세 꼭짓점까지의 거리가 같은 점을 생각할 것이다. 물론, 특수한 경우에는 그게 정답이지만, 일반적인 경우에는 다른 점이 정답이다. 이 점을 페르마 점(Fermat point)라 부르며, 페르마의 마지막 정리로 잘 알려진 그 페르마가 토리첼리에게 보낸 편지에서 처음 제기된 문제였기 때문에 페르마 점이라 부른다. 풀이 자체는 페르마가 아닌 토리첼리가 했다.

찾는 법

한 내각이 120°를 넘는지 여부에 따라 경우가 달라진다.

세 내각이 모두 120° 미만

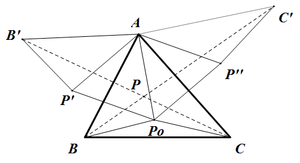
먼저, 삼각형 내부의 한 점 [math]\displaystyle{ P_0 }[/math]를 찍자. 우리가 최소화 하고 싶은 값은 [math]\displaystyle{ \overline{P_0A}+\overline{P_0B}+\overline{P_0C} }[/math]이다. 먼저, [math]\displaystyle{ \triangle{ABP_0} }[/math]를 점 [math]\displaystyle{ A }[/math]를 기준으로 -60도(=300°) 만큼 회전시키고, 새롭게 생긴 삼각형을 [math]\displaystyle{ \triangle{AB'P'} }[/math]라 하자. 그럼, [math]\displaystyle{ \overline{P_0A}=\overline{P'A} }[/math]이고, [math]\displaystyle{ \overline{P_0B}=\overline{P'B'} }[/math]이므로, 최소화하고 싶은 값은 [math]\displaystyle{ \overline{B'P'}+\overline{P'P_0}+\overline{P_0C} }[/math]가 된다. 이 세 선분이 공선점일 때 값이 최소이므로, 페르마 점은 선분 [math]\displaystyle{ \overline{B'C} }[/math]위에 존재한다.

이제, 같은 방법으로 [math]\displaystyle{ \triangle{ACP_0} }[/math]를 회전시킨 삼각형을 [math]\displaystyle{ \triangle{AC'P''} }[/math]라 하자. 그럼, 페르마 점은 선분 [math]\displaystyle{ \overline{C'B} }[/math]위에 존재한다.

따라서, 구하고자 하는 페르마 점은 두 선분의 교점, 그림에서는 [math]\displaystyle{ P }[/math]가 된다.

한 각이 120° 이상

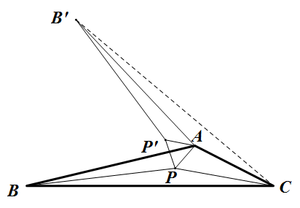
일반성을 잃지 않고 [math]\displaystyle{ \angle{A}\gt 120^\circ }[/math]라 가정하고, 같은 방법을 사용하자. 문제는, 그림에서 알 수 있듯이, 선분 [math]\displaystyle{ \overline{B'C} }[/math]가 삼각형 밖에 존재한다. 또한, 최소화 하고자 하는 값인 [math]\displaystyle{ \overline{B'P'}+\overline{P'P}+\overline{PC} }[/math]는 [math]\displaystyle{ P }[/math]의 위치에 상관없이 [math]\displaystyle{ \overline{B'A}+\overline{AC} }[/math]보다 크거나 같다는 사실을 쉽게 알 수 있다. 따라서, 페르마 점은 [math]\displaystyle{ A }[/math], 즉 120° 이상인 꼭짓점이 된다.

성질

한 각이 120° 이상이면 눈여겨 볼만한 성질이 없기 때문에 세 내각이 모두 120° 미만인 경우만을 고려하기로 하자.

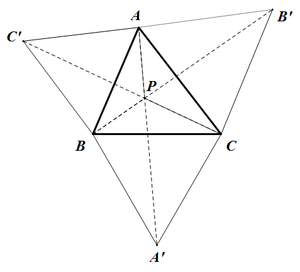
• 작도법은 간단한데, 각 변을 한 변으로 하는 정삼각형을 그려준뒤, 그림처럼 세 선분을 그려주면 그 교점이 페르마 점이다.

  증명은 다음과 같다. 찾는 방법에서, [math]\displaystyle{ \overline{AB}=\overline{AC'} }[/math]이고 [math]\displaystyle{ \angle{BAC'}=60^\circ }[/math]임을 알 수 있다. 따라서, [math]\displaystyle{ \triangle{ABC'} }[/math]는 사이각이 60도인 이등변삼각형이므로, 곧 정삼각형이 된다. 다른 삼각형도 같은 방법으로 정삼각형임을 보일 수 있다.

• 점 A, C', B, P는 공원점이다. 마찬가지로, 점 C, B', A, P랑 점 B, A', C, P도 공원점이다.

  변 [math]\displaystyle{ \overline{AP} }[/math]를 60도 회전시킨 선분을 [math]\displaystyle{ \overline{AP'} }[/math]라 하자. 그럼, 작도가 이루어진 방법과 페르마 점을 찾은 방법에서 점 [math]\displaystyle{ P' }[/math]가 선분 [math]\displaystyle{ \overline{C'P} }[/math]위에 있다는 사실을 알 수 있다. 따라서, [math]\displaystyle{ \angle{APC'}=60^\circ }[/math]. 그런데 [math]\displaystyle{ \triangle{ABC'} }[/math]는 정삼각형이므로, [math]\displaystyle{ \angle{ABC'}=60^\circ }[/math]. 원주각이 성립하므로 점 A, C', B, P는 공원점이다. 같은 방법으로 다른 두 경우도 증명할 수 있다.

• [math]\displaystyle{ \angle{APB}=\angle{BPC}=\angle{CPA}=120^\circ }[/math].

  점 A, C', B, P가 공원점이므로, [math]\displaystyle{ \angle{AC'B}+\angle{APB}=180^\circ }[/math]. 그런데, [math]\displaystyle{ \angle{AC'B}=60^\circ }[/math]이므로 [math]\displaystyle{ \angle{APB}=120^\circ }[/math]. 나머지 두 경우도 같은 방법으로 증명이 된다.

  이 성질로 부터 페르마 점은 세 꼭짓점까지의 각도가 동일한 점이라는 사실을 알 수 있다.

• 세 선분 [math]\displaystyle{ \overline{AA'},\,\overline{BB'},\,\overline{CC'} }[/math]는 한 점에서 만나며, 그 점이 페르마 점이다.

  [math]\displaystyle{ \overline{BB'},\,\overline{CC'} }[/math]의 교점을 [math]\displaystyle{ P }[/math]라 하자. 그럼, 찾는 방법에서 이 점이 페르마 점임을 알 수 있다. 그럼, 증명해야할 것은 세 점 A, P, A'가 공선점이라는 것이다. 먼저, [math]\displaystyle{ \angle{APB}=120^\circ }[/math]임을 보였다. 또한, [math]\displaystyle{ \angle{BPA'}=\angle{BCA'}=60^\circ }[/math]이므로, [math]\displaystyle{ \angle{APB}+\angle{A'PB}=180^\circ }[/math]이다. 따라서, 세 점 A, P, A'는 공선점이다.