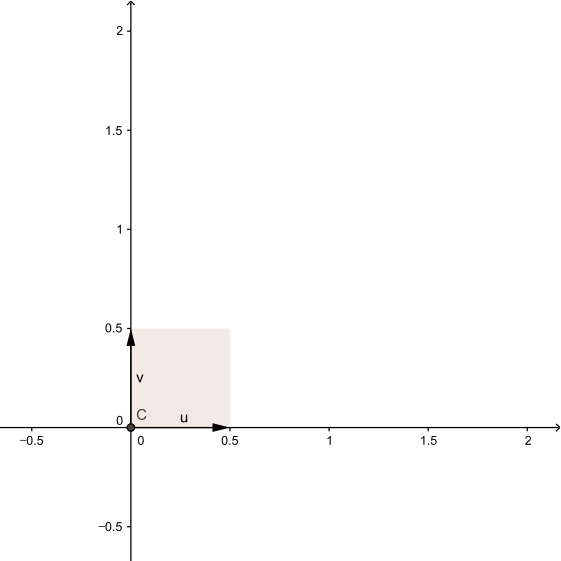선형변환

영어: linear transformation

정의

선형사상은 벡터공간 사이의 보존사상이다. 즉, F-vector space들의 카테고리 [math]\displaystyle{ Vec_F }[/math]의 morphism을 말한다.

구체적으로 정의하자면 다음과 같다.

체 [math]\displaystyle{ F }[/math] 위의 벡터공간 [math]\displaystyle{ V,W }[/math]가 주어지고 [math]\displaystyle{ L }[/math]이 [math]\displaystyle{ V }[/math]에서 [math]\displaystyle{ W }[/math]로의 함수라고 하자. 이때 임의의 [math]\displaystyle{ c\in F }[/math]와 [math]\displaystyle{ \mathbf{v}_1,\mathbf{v}_2\in V }[/math]에 대해

[math]\displaystyle{ L(\mathbf{v}_1+\mathbf{v}_2)=L(\mathbf{v}_1)+L(\mathbf{v}_2) }[/math]

[math]\displaystyle{ L(c\mathbf{v}_1)=cL(\mathbf{v}_1) }[/math]

이면 [math]\displaystyle{ L }[/math]를 [math]\displaystyle{ V }[/math]에서 [math]\displaystyle{ W }[/math]로의 선형변환(linear transformation)이라고 한다. 만약 [math]\displaystyle{ V=W }[/math]이면 선형연산자(linear operator)라고 한다.

또는 다음과 같이 대안적으로 정의하기도 한다: 임의의 [math]\displaystyle{ c_1,c_2\in F }[/math]와 [math]\displaystyle{ \mathbf{v}_1,\mathbf{v}_2\in V }[/math]에 대해

[math]\displaystyle{ L(c_1\mathbf{v}_1+c_2\mathbf{v}_2)=c_1 L(\mathbf{v}_1)+c_2L(\mathbf{v}_2) }[/math]

[math]\displaystyle{ L }[/math]를 [math]\displaystyle{ V }[/math]에서 [math]\displaystyle{ W }[/math]로의 선형변환이라고 한다. 두 정의는 동치이다.

예시

함수 [math]\displaystyle{ L:\mathbb{R}^3 \to \mathbb{R}^2 }[/math]가 다음과 같이 정의되었다고 하자.

[math]\displaystyle{ L\left(\begin{bmatrix} x\\ y\\ z \end{bmatrix}\right)=\begin{bmatrix} x+y\\ y+z \end{bmatrix} }[/math]

그러면

[math]\displaystyle{ \begin{align} L\left(\begin{bmatrix} x_1\\ y_1\\ z_1 \end{bmatrix}+\begin{bmatrix} x_2\\ y_2\\ z_2 \end{bmatrix}\right)&=L\left(\begin{bmatrix} x_1+x_2\\ y_1+y_2\\ z_1+z_2 \end{bmatrix}\right)\\ &=\begin{bmatrix} (x_1+x_2)+(y_1+y_2)\\ (y_1+y_2)+(z_1+z_2) \end{bmatrix}\\ &=\begin{bmatrix} x_1+y_1\\ y_1+z_1 \end{bmatrix}+\begin{bmatrix} x_2+y_2\\ y_2+z_2 \end{bmatrix}\\ &=L\left(\begin{bmatrix} x_1\\ y_1\\ z_1 \end{bmatrix}\right)+L\left(\begin{bmatrix} x_2\\ y_2\\ z_2 \end{bmatrix}\right) \end{align} }[/math]

이고

[math]\displaystyle{ \begin{align} L\left(c\begin{bmatrix} x\\ y\\ z \end{bmatrix}\right)&=L\left(\begin{bmatrix} cx\\ cy\\ cz \end{bmatrix}\right)\\ &=\begin{bmatrix} cx+cy\\ cy+cz \end{bmatrix}\\ &=c\begin{bmatrix} x+y\\ y+z \end{bmatrix}\\ &=cL\left(\begin{bmatrix} x\\ y\\ z \end{bmatrix}\right) \end{align} }[/math]

이므로 [math]\displaystyle{ L }[/math]은 [math]\displaystyle{ \mathbb{R}^3 }[/math]에서 [math]\displaystyle{ \mathbb{R}^2 }[/math]로의 선형변환이다.

일반적으로 [math]\displaystyle{ n \times m }[/math] 행렬 [math]\displaystyle{ A }[/math]에 대해, 함수 [math]\displaystyle{ L:\mathbb{R}^m \to \mathbb{R}^n }[/math]를

[math]\displaystyle{ L(\mathbf{x})=A\mathbf{x} }[/math]

로 정의하면 [math]\displaystyle{ L }[/math]은 선형변환이다. 이 사실을 증명하는 것은 행렬의 성질을 이용해 간단히 할 수 있으므로 독자에게 맡긴다.

시각화

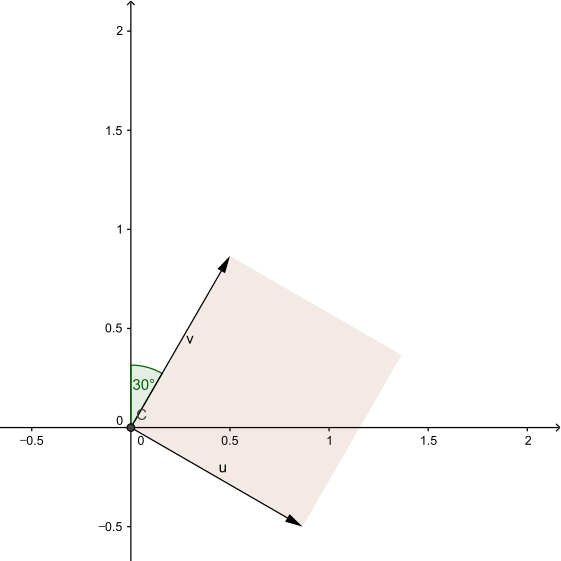
좌표평면의 벡터 [math]\displaystyle{ \mathbf{u},\mathbf{v}\in \mathbb{R}^2 }[/math]를

[math]\displaystyle{ \mathbf{u}=\begin{bmatrix} 1\\ 0 \end{bmatrix},\mathbf{v}=\begin{bmatrix} 0\\ 1 \end{bmatrix} }[/math]

로 정의하고, 집합 [math]\displaystyle{ S }[/math]를

[math]\displaystyle{ S=\{a\mathbf{u}+b\mathbf{v}\in \mathbb{R}^2 : 0\le a \le 1,0\le b\le 1\} }[/math]

로 정의하자. 선형변환 [math]\displaystyle{ L:\mathbb{R}^2 \to \mathbb{R}^2 }[/math]를

[math]\displaystyle{ L(\mathbf{x})=A\mathbf{x} }[/math]

로 정의하자. 아래 표는 [math]\displaystyle{ L }[/math]이 주어졌을 때 [math]\displaystyle{ S }[/math]의 상(image)을 시각적으로 나타낸 것이다.

원본 또는 항등변환, [math]\displaystyle{ A=\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix} }[/math]	2배 확대, [math]\displaystyle{ A=\begin{bmatrix}2 & 0 \\ 0 & 2\end{bmatrix} }[/math]	1/2배로 축소, [math]\displaystyle{ A=\begin{bmatrix}\frac{1}{2} & 0 \\ 0 & \frac{1}{2}\end{bmatrix} }[/math]
x축 대칭, [math]\displaystyle{ A=\begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix} }[/math]	y축 대칭, [math]\displaystyle{ A=\begin{bmatrix}-1 & 0 \\ 0 & 1\end{bmatrix} }[/math]	시계방향으로 30° 회전, [math]\displaystyle{ A=\begin{bmatrix}\frac{\sqrt{3}}{2} & \frac{1}{2} \\ -\frac{1}{2} & \frac{\sqrt{3}}{2}\end{bmatrix} }[/math]

성질

선형변환 [math]\displaystyle{ L:V\to W }[/math]와 [math]\displaystyle{ \mathbf{u},\mathbf{v}\in V }[/math]에 대해,

• [math]\displaystyle{ L(\mathbf{0}_V)=\mathbf{0}_W }[/math]

[math]\displaystyle{ \mathbf{0}_V=\mathbf{0}_V+\mathbf{0}_V }[/math]이므로 선형변환의 정의에 의해

[math]\displaystyle{ \begin{align} L(\mathbf{0}_V)&=L(\mathbf{0}_V+\mathbf{0}_V)\\ &=L(\mathbf{0}_V)+L(\mathbf{0}_V) \end{align} }[/math]

이다. 양변의 [math]\displaystyle{ L(\mathbf{0}_V) }[/math]를 소거하면 원하는 결론을 얻는다.

• [math]\displaystyle{ L(-\mathbf{v})=-L(\mathbf{v}) }[/math]

[math]\displaystyle{ \begin{align} L(-\mathbf{v})&=L((-1_F)\mathbf{v})\\ &=(-1_F)L(\mathbf{v})\\ &=-L(\mathbf{v}) \end{align} }[/math]

이므로 원하는 결론을 얻는다.

• [math]\displaystyle{ L(\mathbf{u}-\mathbf{v})=L(\mathbf{u})-L(\mathbf{v}) }[/math]

[math]\displaystyle{ \begin{align} L(\mathbf{u}-\mathbf{v})&=L(\mathbf{u}+(-\mathbf{v}))\\ &=L(\mathbf{u})+L(-\mathbf{v})\\ &=L(\mathbf{u})-L(\mathbf{v}) \end{align} }[/math]

이므로 원하는 결론을 얻는다.

선형변환의 핵과 치역

체 [math]\displaystyle{ F }[/math] 위의 벡터공간 [math]\displaystyle{ V,W }[/math]와 선형변환 [math]\displaystyle{ L:V\to W }[/math]가 주어졌다고 하자. 이때, 집합

[math]\displaystyle{ \ker L = \{\mathbf{v}\in V: L(\mathbf{v})=\mathbf{0}_W\} }[/math]

을 [math]\displaystyle{ L }[/math]의 핵(kernel)이라고 하고, 집합

[math]\displaystyle{ \operatorname{ran}L = \{\mathbf{w}\in W: \mathbf{w}=L(\mathbf{v})\text{ for some }\mathbf{v}\in V\} }[/math]

을 [math]\displaystyle{ L }[/math]의 치역(range)이라고 한다.

[math]\displaystyle{ \ker L }[/math]은 [math]\displaystyle{ V }[/math]의 부분공간이다. [math]\displaystyle{ \ker L }[/math]의 임의의 두 원소를 [math]\displaystyle{ \mathbf{u},\mathbf{v} }[/math]라고 하면 [math]\displaystyle{ \ker L }[/math]의 정의에 의해 [math]\displaystyle{ L(\mathbf{u})=L(\mathbf{v})=\mathbf{0} }[/math]이다. 그러면 선형변환의 정의에 의해 [math]\displaystyle{ L(\mathbf{u}+\mathbf{v})=\mathbf{0} }[/math]이므로 [math]\displaystyle{ \mathbf{u}+\mathbf{v}\in \ker L }[/math]이다. 또한 임의의 [math]\displaystyle{ c\in F }[/math]에 대해

[math]\displaystyle{ \begin{align} L(c\mathbf{v})&=cL(\mathbf{v})\\ &=c\mathbf{0}_W\\ &=\mathbf{0}_W \end{align} }[/math]

이므로 [math]\displaystyle{ c\mathbf{v}\in \ker L }[/math]이다. 따라서 원하는 결론을 얻는다.

[math]\displaystyle{ \operatorname{ran}L }[/math]는 [math]\displaystyle{ W }[/math]의 부분공간이다. [math]\displaystyle{ \operatorname{ran} L }[/math]의 임의의 두 원소를 [math]\displaystyle{ \mathbf{v}_1,\mathbf{v}_2 }[/math]라고 하면 [math]\displaystyle{ \operatorname{ran}L }[/math]의 정의에 의해 [math]\displaystyle{ \mathbf{v}_1=L(\mathbf{u}_1),\mathbf{v}_2=L(\mathbf{u}_2) }[/math]인 [math]\displaystyle{ \mathbf{u}_1,\mathbf{u}_2\in V }[/math]가 존재한다. 그러면

[math]\displaystyle{ \begin{align} \mathbf{v}_1+\mathbf{v}_2&=L(\mathbf{u}_1)+L(\mathbf{u}_2)\\ &=L(\mathbf{u}_1+\mathbf{u}_2) \end{align} }[/math]

이고 [math]\displaystyle{ \mathbf{u}_1+\mathbf{u}_2\in V }[/math]이므로 [math]\displaystyle{ \mathbf{v}_1+\mathbf{v}_2=L(\mathbf{u}^*) }[/math]인 [math]\displaystyle{ \mathbf{u}^*\in V }[/math]가 존재하고, 그러므로 [math]\displaystyle{ \mathbf{v}_1+\mathbf{v}_2\in \operatorname{ran} L }[/math]이다. 또한 임의의 [math]\displaystyle{ c\in F }[/math]에 대해

[math]\displaystyle{ \begin{align} c\mathbf{v}_1&=cL(\mathbf{u}_1)\\ &=L(c\mathbf{u}_1) \end{align} }[/math]

이고 [math]\displaystyle{ c\mathbf{u}_1\in V }[/math]이므로 [math]\displaystyle{ c\mathbf{v}_1=L(\mathbf{u}^*) }[/math]인 [math]\displaystyle{ \mathbf{u}^*\in V }[/math]가 존재하고, 그러므로 [math]\displaystyle{ c\mathbf{v}_1\in \operatorname{ran} L }[/math]이다. 따라서 원하는 결론을 얻는다.

[math]\displaystyle{ \ker L }[/math]와 [math]\displaystyle{ \operatorname{ran} L }[/math] 사이에는 다음 관계식이 성립한다.

[math]\displaystyle{ \dim V=\dim \ker L + \dim \operatorname{ran} L }[/math]

[math]\displaystyle{ \dim \ker L=k }[/math]라고 하자. [math]\displaystyle{ \{\mathbf{v}_1,\mathbf{v}_2,\cdots, \mathbf{v}_k\} }[/math]를 [math]\displaystyle{ \ker K }[/math]의 기저라고 하자. [math]\displaystyle{ \dim V=n }[/math]이라 하면, [math]\displaystyle{ \ker K }[/math]가 [math]\displaystyle{ V }[/math]의 부분공간이므로 [math]\displaystyle{ \mathbf{v}_{k+1},\mathbf{v}_{k+2},\cdots, \mathbf{v}_n\in V }[/math]를 적당히 골라 [math]\displaystyle{ \{\mathbf{v}_1,\cdots,\mathbf{v}_k,\mathbf{v}_{k+1},\cdots,\mathbf{v}_n\} }[/math]이 [math]\displaystyle{ V }[/math]의 기저가 되도록 할 수 있다. 이제 [math]\displaystyle{ \mathbf{w}\in \operatorname{ran}L }[/math]이라 하면 [math]\displaystyle{ \operatorname{ran}L }[/math]의 정의에 의해

[math]\displaystyle{ \mathbf{w}=L(\mathbf{v}) }[/math]

인 [math]\displaystyle{ \mathbf{v}\in V }[/math]가 존재한다. 이때 상수 [math]\displaystyle{ c_1,\cdots,c_n }[/math]에 대해

[math]\displaystyle{ \mathbf{v}=c_1\mathbf{v}_1+\cdots+c_k \mathbf{v}_k+c_{k+1}\mathbf{v}_{k+1}+\cdots+c_n\mathbf{v}_n }[/math]

이므로

[math]\displaystyle{ \begin{align} L(\mathbf{v})&=L(c_1\mathbf{v}_1+\cdots+c_k \mathbf{v}_k+c_{k+1}\mathbf{v}_{k+1}+c_n\mathbf{v}_n)\\ &=c_1L(\mathbf{v}_1)+\cdots++c_k L(\mathbf{v}_k)+c_{k+1}L(\mathbf{v}_{k+1})+\cdots+c_nL(\mathbf{v}_n)\\ &=\mathbf{0}_W+\cdots+\mathbf{0}_W+c_{k+1}L(\mathbf{v}_{k+1})+\cdots+c_nL(\mathbf{v}_n)\\ &=c_{k+1}L(\mathbf{v}_{k+1})+\cdots+c_nL(\mathbf{v}_n) \end{align} }[/math]

이다. 그러므로 [math]\displaystyle{ \{L(\mathbf{v}_{k+1}),\cdots,L(\mathbf{v}_n)\} }[/math]은 [math]\displaystyle{ \operatorname{ran}L }[/math]을 생성한다. 이제 [math]\displaystyle{ L(\mathbf{v}_{k+1}),\cdots,L(\mathbf{v}_n) }[/math]가 선형독립임을 보이자. 방정식

[math]\displaystyle{ x_{k+1} L(\mathbf{v}_{k+1})+\cdots+x_n L(\mathbf{v}_n)=\mathbf{0}_W }[/math]

에 대해

[math]\displaystyle{ L(x_{k+1}\mathbf{v}_{k+1}+\cdots+x_n\mathbf{v}_n)=\mathbf{0}_W }[/math]

이므로

[math]\displaystyle{ x_{k+1}\mathbf{v}_{k+1}+\cdots+x_n\mathbf{v}_n\in \ker L }[/math]

이다. 따라서 상수 [math]\displaystyle{ d_1,\cdots,d_k }[/math]에 대해

[math]\displaystyle{ x_{k+1}\mathbf{v}_{k+1}+\cdots+x_n\mathbf{v}_n=d_1 \mathbf{v}_1+\cdots+d_k \mathbf{v}_k }[/math]

이며 [math]\displaystyle{ \mathbf{v}_1,\cdots,\mathbf{v}_n }[/math]은 선형독립이므로 [math]\displaystyle{ x_{k+1}=\cdots=x_n=d_1=\cdots=d_k=0 }[/math]이어야 한다. 따라서 [math]\displaystyle{ L(\mathbf{v}_{k+1}),\cdots,L(\mathbf{v}_n) }[/math]는 선형독립이며 [math]\displaystyle{ \{L(\mathbf{v}_{k+1}),\cdots,L(\mathbf{v}_n)\} }[/math]은 [math]\displaystyle{ \operatorname{ran}L }[/math]의 기저이고, [math]\displaystyle{ \dim\operatorname{ran}L=n-k }[/math]임을 안다. 따라서 원하는 결론을 얻는다.