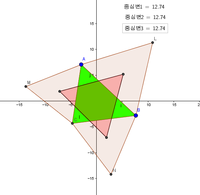
나폴레옹의 정리(Napoleon's theorem, -定理)는 유명한 프랑스 황제 나폴레옹 보나파르트의 이름이 붙어 있는 기하학의 정리이다. 이 정리는 다음과 같이 기술할 수 있다.
- 임의의 삼각형에 각 변에 그 길이를 한 변의 길이로 하는 정삼각형 세 개를 덧그릴 때, 각 정삼각형의 무게중심을 이으면 정삼각형이 만들어진다. 여기서 삼각형을 덧그릴 때 셋 모두 원 삼각형의 바깥으로 덧그리거나(오른쪽 그림) 모두 원 삼각형의 안쪽으로 덧그려야 한다.
나폴레옹의 삼각형[편집 | 원본 편집]
이 정리가 정삼각형임을 보장하는 새로운 삼각형은 나폴레옹의 삼각형(Napoleon's triangle)이라 하는데, 바깥쪽에 덧그리는 경우는 바깥쪽 나폴레옹의 삼각형(outer Napoleon's triangle), 안쪽에 덧그리는 경우는 안쪽 나폴레옹의 삼각형(inner Napoleon's triangle)이라 부른다. 바깥쪽과 안쪽 나폴레옹의 삼각형 간의 넓이의 차는 원래 삼각형의 넓이와 같다. 두 나폴레옹의 삼각형은 같은 중심을 가지며, 이는 원 삼각형의 무게 중심과 같다.
증명법[편집 | 원본 편집]
이 정리를 처음으로 제출한 사람은 나폴레옹 1세로 알려져 있으나, 이에 관한 명확한 증거 사료는 없다. 증명은 여러 방법이 고안되어 있는데 복소평면을 이용하면 쉽게 할 수 있다.[1][2][3]
편의상 삼각형의 꼭짓점을 복소평면 상의 복소수 [math]\displaystyle{ A= z_1 ,B= z_2 }[/math]로 놓고 나머지 한 꼭짓점이 복소수 [math]\displaystyle{ C= -z_1 - z_2 }[/math]가 되게 놓는다. ABC가 시계방향으로 놓이든 반시계방향으로 놓이든 상관 없다. 편의상 반시계방향으로 놓인다고 가정을 한다. 평행이동으로 삼각형의 무게중심을 원점으로 놓을 수 있다.
그러면 변 [math]\displaystyle{ \bar{AB} }[/math]를 기준으로 뻗은 삼각형을 한 변으로 하는 정삼각형의 나머지 한 꼭짓점의 좌표를 구해보자. 일단 정삼각형 변의 벡터의 좌표는 [math]\displaystyle{ B-A= z_2 -z_1 }[/math]이고, 변의 길이가 1인 정삼각형의 높이는 [math]\displaystyle{ \sqrt{3}/2 }[/math]이다. 또한 AB가 반시계방향으로 배열되어 있을 때 바깥쪽 정삼각형의 꼭짓점의 좌표는 AB의 중점을 기준으로 AB를 시계방향으로 π/2만큼 회전한 형태가 된다. 또한 정삼각형의 무게중심은 AB의 중점 X과 새 꼭짓점 D를 잇는 선분의 XY-1:2등분점이다. 따라서 정삼각형 △ABD의 무게중심 G에 대해서 XG의 길이는 AB의 길이의 [math]\displaystyle{ \sqrt{3}/6 }[/math]가 된다.
복소평면의 곱의 공식 [math]\displaystyle{ r_1 {e}^{i \theta_1} \cdot r_2 {e}^{i \theta_2} = r_1 r_2 {e}^ {i ( \theta_1 + \theta_2 ) } }[/math]를 이용하면 XG를 복소수로 표현할 경우 [math]\displaystyle{ \vec{XG} = (B-A) \times \left( - \sqrt{3} i/6 \times e^{-\pi/2} \right) }[/math] 여기서 [math]\displaystyle{ i }[/math]를 허수의 단위이다.
따라서 정삼각형 △ABD의 점 G의 좌표는 [math]\displaystyle{ G= X+\vec{XG} = \frac{z_1 +z_2}{2} - \frac{(z_2 - z_1 ) \sqrt{3} i}{6} = \frac{ ( 3+ \sqrt{3} i )z_1 + (3 - \sqrt{3} i )z_2 }{6} }[/math] 가 된다.
위와 마찬가지로 변 BC를 한 변으로 하고 삼각형 △ABC 바깥으로 표시된 정삼각형 △BCE의 무게중심 H의 좌표는 [math]\displaystyle{ \frac{(-z_1 -z_2) + z_2 }{2} - \frac{ (-(z_2 +z_1 ) - z_2 ) \sqrt{3} i }{6} = \frac{ (-3+ \sqrt{3} i)z_1 + ( 2\sqrt{3} i )z_2 }{6} }[/math].
변 CA를 한 변으로 하고 삼각형 △ABC 바깥으로 표시된 정삼각형 △CAF의 무게중심 I의 좌표는 [math]\displaystyle{ \frac{z_1 + (-z_1 -z_2)}{2} - \frac{ ( z_1 -( -z_1 - z_2 ) ) \sqrt{3} i }{6} = \frac{ ( - 2 \sqrt{3} i)z_1 + (-3 - \sqrt{3} i )z_2 }{6} }[/math].
분명 삼각형 △GHI의 무게중심은 원점, 즉 복소평면의 0에 해당하는 점이다.
이제 이 점이 삼각형 △GHI의 외심임을 보이면 된다. 즉 G, H, I를 복소평면의 좌표로 표현했을 때 |G| = |H| = |I|임을 보이면 된다. 왜냐하면 삼각형 GHI의 무게중심 P에 대해서 GP=HP면 변 I에서 GH에 내리는 중선은 GH가 수직이 된다. 수직이 아니면 G, H의 중점 M에 대해 GM=HM, MP는 공통변이므로 제2코사인 법칙에 의해 GP와 HP의 길이가 달라질 수밖에 없다. 따라서 △IMG=△IMH, 즉 IG=IH이다. 마찬가지 방법으로 보이면 GH=GI이므로 외심과 무게중심이 일치하면 정삼각형이 된다.
그런데 [math]\displaystyle{ {\left| \frac{ ( 3+ \sqrt{3} i )z_1 + (3 - \sqrt{3} i )z_2 }{6} \right| }^2 = 1/3 ( {|z_1 |}^2 + {|z_2 |}^2 ) + \frac{6 + 6 \sqrt{3} i}{36} (z_1 \bar{z_2 } ) + \frac{6 - 6 \sqrt{3} i}{36} (\bar{z_1 } z_2 ) }[/math], [math]\displaystyle{ {\left| \frac{ (-3+ \sqrt{3} i)z_1 + ( 2\sqrt{3} i )z_2 }{6} \right| }^2= 1/3 ( {|z_1 |}^2 + {|z_2 |}^2 ) + \frac{6 + 6 \sqrt{3} i}{36} (z_1 \bar{z_2 } ) + \frac{6 - 6 \sqrt{3} i}{36} (\bar{z_1 } z_2 ) }[/math], [math]\displaystyle{ {\left| \frac{ - 2 \sqrt{3} i)z_1 + (-3 - \sqrt{3} i )z_2 }{6} \right| }^2= 1/3 ( {|z_1 |}^2 + {|z_2 |}^2 ) + \frac{6 + 6 \sqrt{3} i}{36} (z_1 \bar{z_2 } ) + \frac{6 - 6 \sqrt{3} i}{36} (\bar{z_1 } z_2 ) }[/math], 따라서 OG=OH=OI가 성립하며, △GHI는 정삼각형이다.
관련 문서[편집 | 원본 편집]
외부 링크[편집 | 원본 편집]
각주