톨레미의 정리

개요

그리스의 천문학자 프톨레마이오스의 이름이 붙은 평면기하학의 정리 중 하나이다. 그런데 어째서인지 한국에선 "프톨레마이오스의 정리" 보다는 영어식 발음인 "톨레미의 정리"라는 이름으로 더 많이 알려져 있다. 톨레미의 정리는 원에 내접하는 사각형에 관한 것이며, 삼각형의 닮음과 원의 성질만 배우면 바로 증명이 가능할 정도로 간단하다. 하지만 한국의 수학 교육과정에서는 가르치지 않고 수학 경시대회를 준비한다면 학원 같은 곳에서 배우게 된다. 하지만 비단 수학 경시대회가 아니더라도 이 톨레미의 정리는 알아놓으면 고등학교 때 까지도 잘만 써먹는다.

정리

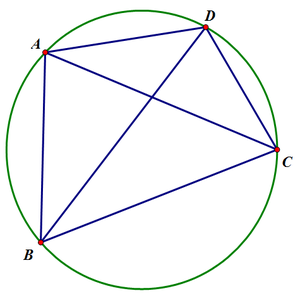
원에 내접하는 사각형에서, [math]\displaystyle{ \overline{AB}\cdot\overline{CD}+\overline{AD}\cdot\overline{BC}=\overline{AC}\cdot\overline{BD} }[/math]이 성립한다. 다른 말로 표현하자면, 내접사각형의 두 대각선 길이의 곱은 두 쌍의 대변의 길이의 곱의 합이다.

증명

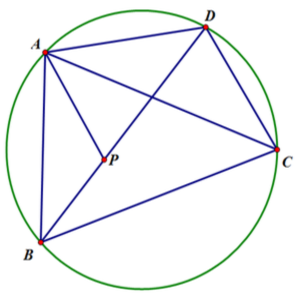
[math]\displaystyle{ \angle{CAD}=\angle{BAP} }[/math]가 되게 대각선 [math]\displaystyle{ \overline{BD} }[/math]위에 점 [math]\displaystyle{ P }[/math]를 잡는다. 또한, 원주 [math]\displaystyle{ \overarc{AD} }[/math]에 대한 원주각에 의해 [math]\displaystyle{ \angle{ABP}=\angle{ACD} }[/math]이다. [math]\displaystyle{ \therefore\triangle{ABP}\sim\triangle{ACD} }[/math] (AA 닮음). 변의 비를 구하면, [math]\displaystyle{ \overline{AB}:\overline{BP}=\overline{AC}:\overline{CD} }[/math]이고, 따라서 [math]\displaystyle{ \overline{AB}\cdot\overline{CD}=\overline{AC}\cdot\overline{BP}\quad\cdots\left(1\right) }[/math] 이제 [math]\displaystyle{ \angle{BAC}=\angle{PAD} }[/math]이고, [math]\displaystyle{ \angle{BCA}=\angle{BDA} }[/math] (원주 [math]\displaystyle{ \overarc{AB} }[/math]에 대한 원주각)이므로 [math]\displaystyle{ \triangle{ABC}\sim\triangle{APD} }[/math] (AA 닮음). 변의 비를 구하면, [math]\displaystyle{ \overline{AC}:\overline{BC}=\overline{AD}:\overline{PD} }[/math]이고, 따라서 [math]\displaystyle{ \overline{BC}\cdot\overline{AD}=\overline{AC}\cdot\overline{PD}\quad\cdots\left(2\right) }[/math]. 1번식과 2번식을 변끼리 더하면, [math]\displaystyle{ \overline{AB}\cdot\overline{CD}+\overline{AD}\cdot\overline{BC}=\overline{AC}\left(\overline{BP}+\overline{PD}\right)=\overline{AC}\cdot\overline{BD} }[/math].

톨레미의 정리의 역

볼록사각형에서 두 쌍의 대변의 곱의 합이 두 대각선의 곱과 같으면 그 사각형은 원에 내접한다. 즉, [math]\displaystyle{ \overline{AB}\cdot\overline{CD}+\overline{AD}\cdot\overline{BC}=\overline{AC}\cdot\overline{BD} }[/math]이 성립하면 [math]\displaystyle{ A,B,C,D }[/math]는 공원점이다.

증명

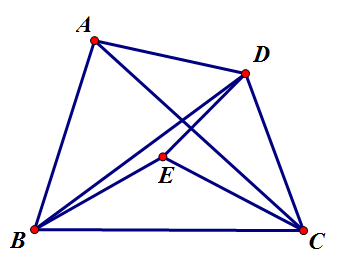
[math]\displaystyle{ \angle{BCE}=\angle{ACD},\,\angle{EBC}=\angle{DAC} }[/math]가 되게 점 [math]\displaystyle{ E }[/math]를 사각형 내부에 잡는다. 그러면 [math]\displaystyle{ \triangle{BCE}\sim\triangle{ACD} }[/math](AA 닮음)이다. 따라서,

[math]\displaystyle{ \overline{AD}\cdot\overline{BC}=\overline{AC}\cdot\overline{BE}\quad\cdots1 }[/math]

또한, [math]\displaystyle{ \overline{EC}:\overline{BC}=\overline{DC}:\overline{AC} }[/math]이고, [math]\displaystyle{ \angle{ECD}=\angle{ACB} }[/math]이므로 [math]\displaystyle{ \triangle{DCE}\sim\triangle{ABC} }[/math](SAS 닮음)이다. 따라서,

[math]\displaystyle{ \overline{AB}\cdot\overline{DC}=\overline{AC}\cdot\overline{DE}\quad\cdots2 }[/math]이고,

[math]\displaystyle{ \angle{CDE}=\angle{CAB}\quad\cdots3 }[/math].

1번과 2번 식을 변끼리 더하면 [math]\displaystyle{ \overline{AB}\cdot\overline{CD}+\overline{AD}\cdot\overline{BC}=\overline{AC}\left(\overline{BE}+\overline{DE}\right) }[/math]이다. 이 식을 처음 가정과 비교하면, [math]\displaystyle{ \overline{BE}+\overline{DE}=\overline{BD} }[/math]이고, 따라서 [math]\displaystyle{ B,E,D }[/math]는 공선점이다. 또한, 3번 식으로 부터, [math]\displaystyle{ \angle{CDB}=\angle{CAB} }[/math]이다. 원주각이 성립하므로, [math]\displaystyle{ A,B,C,D }[/math]는 공원점이다.

톨레미의 부등식

임의의 사각형에서, [math]\displaystyle{ \overline{AB}\cdot\overline{CD}+\overline{AD}\cdot\overline{BC}\geq\overline{AC}\cdot\overline{BD} }[/math]가 성립한다. 등호가 성립할 필요충분조건은 사각형이 원에 내접할 때. 그런데 신기한 것은, 이 톨레미의 부등식은 평면 뿐만이 아니라 모든 차원의 사각형에 대해 성립한다! 증명은 다음과 같다.

증명

벡터 [math]\displaystyle{ \vec{a},\vec{b},\vec{c},\vec{d} }[/math]에 대해, [math]\displaystyle{ \left(\vec{a}-\vec{b}\right)\cdot\left(\vec{c}-\vec{d}\right)+\left(\vec{a}-\vec{d}\right)\cdot\left(\vec{b}-\vec{c}\right)=\vec{a}\cdot\vec{b}-\vec{a}\cdot\vec{d}-\vec{b}\cdot\vec{c}+\vec{c}\cdot\vec{d}=\left(\vec{a}-\vec{c}\right)\cdot\left(\vec{b}-\vec{d}\right) }[/math]이므로로, 삼각부등식에 의해, [math]\displaystyle{ \left|\left(\vec{a}-\vec{b}\right)\cdot\left(\vec{c}-\vec{d}\right)\right|+\left|\left(\vec{a}-\vec{d}\right)\cdot\left(\vec{b}-\vec{c}\right)\right|\geq\left|\left(\vec{a}-\vec{c}\right)\cdot\left(\vec{b}-\vec{d}\right)\right| }[/math]가 성립한다. 이는 곧, [math]\displaystyle{ \left|\vec{a}-\vec{b}\right|\cdot\left|\vec{c}-\vec{d}\right|+\left|\vec{a}-\vec{d}\right|\cdot\left|\vec{b}-\vec{c}\right|\geq\left|\vec{a}-\vec{c}\right|\cdot\left|\vec{b}-\vec{d}\right| }[/math]이고, 따라서 [math]\displaystyle{ \overline{AB}\cdot\overline{CD}+\overline{AD}\cdot\overline{BC}\geq\overline{AC}\cdot\overline{BD} }[/math]가 성립한다.

여기서 등호가 성립한다면 톨레미의 정리의 역이 성립한다는 뜻이고, 따라서 네 점은 공원점이다. 역으로 네 점이 한 원 위에 있으면 톨레미의 정리로 부터 등호가 성립한다.

관련 항목

• 원 (도형)
• 닮음
• 방멱의 정리