잔글편집 요약 없음 |
잔글 (→Dual) |
||
| 27번째 줄: | 27번째 줄: | ||
== Dual == | == Dual == | ||
{{참조|쌍대 (범주론)}} | |||
범주 <math>\mathcal C</math>의 '''범주론적 쌍대'''(categorical dual) 또는 '''반대 범주'''(opposite category)는 화살표의 방향을 모두 거꾸로 한 category를 말한다. | |||
== 범주의 예 == | == 범주의 예 == | ||
2016년 10월 9일 (일) 21:27 판
틀:학술
수학에서, 범주(category, 줄여서 cat)는 특별한 집합과 연산을 추상화한 대수적 구조를 한번 더 추상화한 것이다. 모든 대수적 구조에 공통적으로 나타나는 '집합들'(object)과 '함수들'(morphism)을 가지고 있으며, 이 범주들 사이에 주어진 대응인 함자(functors)와 그 함자들 사이의 자연 변환(natural transformation)이 있다. Functors와 natural transformations는 다시 category를 이룬다.
범주론의 창시자인 Eilenberg와 Mac Lane에 따르면, category는 functor 때문에 만들었고, functor는 natural transformation 때문에 만들었다고 한다.[1] Mac Lane은 category theory의 아이디어를 homology의 공리화 과정에서 얻었다고 한다.
정의
범주(category)[2]는 메타-범주(metacategory)의 집합론적 표현이다. 더 자세하게는 category는 항등함수(identity)와 함수의 합성(composition)을 가진 유향 그래프(directed graph, 또는 diagram scheme)이다. 즉, category [math]\displaystyle{ \mathcal C }[/math]는 다음과 같은 데이터로 구성된다:
- 모든 대상(object)들의 모임(class) [math]\displaystyle{ \operatorname{ob}(\mathcal C) }[/math].[3]
- 모든 화살표(arrow, 또는 morphism, map)들의 모임(class) [math]\displaystyle{ \operatorname{hom}(\mathcal C) = \bigcup_{a, b \in \operatorname{ob}(\mathcal C)} \operatorname{hom}(a, b) }[/math].[4]
- 정의역 연산자 [math]\displaystyle{ \operatorname{dom}: \; \operatorname{hom}(\mathcal C) \to \operatorname{ob}(\mathcal C) }[/math]
- 공역 연산자 [math]\displaystyle{ \operatorname{cod}: \; \operatorname{hom}(\mathcal C) \to \operatorname{ob}(\mathcal C) }[/math]
- 정의역이 [math]\displaystyle{ a }[/math], 공역이 [math]\displaystyle{ b }[/math]인 화살표를 [math]\displaystyle{ f: \; a \to b }[/math]로 표기하고, class [math]\displaystyle{ \operatorname{hom}(a, b) = \{ f \in \operatorname{hom}(\mathcal C): \; \operatorname{dom} f = a, \; \operatorname{cod} f = b \} }[/math]로 정의한다.
- 합성 가능한 짝(composable pair)들의 모임 [math]\displaystyle{ \operatorname{hom}(\mathcal C) \times_O \operatorname{hom}(\mathcal C) = \{ (g, f): \; \operatorname{dom} g = \operatorname{cod} f\} }[/math]
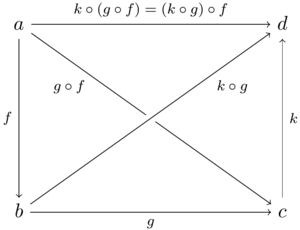
- 합성 연산자 [math]\displaystyle{ \circ: \operatorname{hom}(\mathcal C) \times_O \operatorname{hom}(\mathcal C) \to \operatorname{hom}(\mathcal C) }[/math]
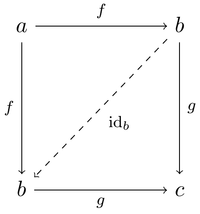
- 항등함수 연산자 [math]\displaystyle{ \operatorname{id}_\bullet: \operatorname{ob}(\mathcal C) \to \operatorname{hom}(\mathcal C) }[/math]
- 항등함수는 합성 연산에 대한 항등원으로 작용해야 한다. 즉, 다음 그림이 가환해야 한다.
작은 범주와 큰 범주
- [math]\displaystyle{ \operatorname{ob}(\mathcal C) }[/math]와 [math]\displaystyle{ \operatorname{hom}(\mathcal C) }[/math]이 모두 집합일 때, [math]\displaystyle{ \mathcal C }[/math]는 작은 범주(small category)라고 한다.
- 작은 범주가 아니면 큰 범주(large category)라고 한다.
- 큰 범주 중에서, 모든 [math]\displaystyle{ a, b\in \operatorname{ob}(\mathcal C) }[/math]에 대해 [math]\displaystyle{ \operatorname{hom}(a, b) }[/math]가 집합일 때, [math]\displaystyle{ \mathcal C }[/math]는 국소적으로 작은 범주(locally small category)라고 한다. 여기서 '국소적'은 전체 morphism들의 모임이 아닌 [math]\displaystyle{ \operatorname{hom}(a, b) }[/math]를 보았을 때를 의미하는 것이다. 이때 각각의 [math]\displaystyle{ \operatorname{hom}(a, b) }[/math]를 homset이라고 한다.
Large category는 상대적으로 다루기가 어렵다. 그래도 locally small이면 그나마 나은 편이다. 많은 수학적으로 의미 있는 category들은 locally small이다.
Dual
범주 [math]\displaystyle{ \mathcal C }[/math]의 범주론적 쌍대(categorical dual) 또는 반대 범주(opposite category)는 화살표의 방향을 모두 거꾸로 한 category를 말한다.