편집 요약 없음 |
|||
| (사용자 7명의 중간 판 19개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
[[파일:Circle radians.gif|섬네일|300px]] | [[파일:Circle radians.gif|섬네일|300px]] | ||
[[부채꼴]]의 반지름과 호의 길이가 같을 때 중심각의 크기를 | '''라디안(radian)'''은 각도 단위 중 하나로, [[부채꼴]]의 반지름과 호의 길이가 같을 때 중심각의 크기를 '''1라디안'''이라고 하고, <math>1\operatorname{rad}</math>로 쓴다. 보통 <math>\operatorname{rad}</math>는 생략한다. 예를 들어, <math>\sin (1\operatorname{rad})</math>은 <math>\sin 1</math>로 간단하게 표기한다. | ||
== 역사 == | |||
라디안이라는 표현이 사용된 것은 비교적 최근으로 알려져 있다. | |||
[[파일:Roger cotes.jpg|섬네일|로저 코츠의 초상]] | |||
호도, 즉 부채꼴의 반지름의 길이와 호의 길이가 같을 때 그 부채꼴의 중심각의 각도라는 개념 자체는 [[1917년]] 영국의 수학자였던 로저 코츠(Roger Cotes, [[1682년]] [[7월 10일]]~[[1716년]] [[6월 5일]])에 의해 이미 사용되고 있었다. 다만 어디까지나 개념만 언급한 것이지, 라디안이라는 이름까진 언급하진 않고 있다.<ref>http://www-groups.dcs.st-and.ac.uk/~history/Printonly/Cotes.html</ref> | |||
현재까지 남겨진 기록 중 라디안이라는 이름이 처음으로 등장하기 시작한 것은 [[1873년]] [[6월 5일]] [[위키백과:퀸스 대학교 벨파스트|퀸스 대학교 벨파스트]]의 물리학자였던 제임스 톰슨(James Thomson)이 낸 시험 문제에서의 등장이 처음이라고 한다. [[카더라 통신]]에 의하면 원래 제임스 톰슨이 라디안이라는 표현을 쓴 것은 그보다 훨씬 전인 [[1871년]]부터였지만. | |||
[[위키백과:세인트앤드루스 대학교|세인트앤드루스 대학교]]의 교수였던 [[토머스 뮤어]]는 [[1869년]] 내내 '이 부채꼴의 반지름의 길이와 호의 길이가 같을 때 그 부채꼴의 중심각의 각도'의 이름을 라드(rad), 라디알(radial), 라디안(radian) 중에서 뭘로 정할지 고민했었다고 한다. | |||
이후 6년이라는 긴 시간이 지난 [[1874년]]이 되어서야 토머스 뮤어는 이 특수한 각의 명칭을 제임스 톰슨과의 상의 끝에 라디안으로 채택하게 된다.<ref>카조리 플로리안, [[1929년]], History of Mathematical Notations 2. pp.147–148, {{ISBN|0-486-67766-4}}.</ref> | |||
== 60분법과의 관계 == | == 60분법과의 관계 == | ||
| 10번째 줄: | 19번째 줄: | ||
첫번째로, [[원주율]]에 대해서 명심할 사실이 있는데 '''π×(원의 지름)=(원의 둘레)라는 사실이다.''' 양변에 똑같이 2를 나눠보면 π×(원의 지름)/2=(원의 둘레)/2가 되므로 π×(원의 반지름)=(반원의 호의 길이)가 된다. | 첫번째로, [[원주율]]에 대해서 명심할 사실이 있는데 '''π×(원의 지름)=(원의 둘레)라는 사실이다.''' 양변에 똑같이 2를 나눠보면 π×(원의 지름)/2=(원의 둘레)/2가 되므로 π×(원의 반지름)=(반원의 호의 길이)가 된다. | ||
두번째로, '''[[부채꼴]]에서 중심각의 크기는 그 부채꼴의 호의 길이에 비례한다는 사실'''이다. | 두번째로, '''[[부채꼴]]에서 중심각의 크기는 그 부채꼴의 호의 길이에 비례한다는 사실'''이다. | ||
세번째로, '''중심각이 1rad인 부채꼴의 호의 길이는 반지름과 같다.'''이다. | 세번째로, '''중심각이 1rad인 부채꼴의 호의 길이는 반지름과 같다.'''이다. | ||
따라서<br> | 따라서<br /> | ||
π×(원의 반지름):π×1rad=(반원의 호의 길이):(반원의 중심각의 크기)<br> | π×(원의 반지름):π×1rad=(반원의 호의 길이):(반원의 중심각의 크기)<br /> | ||
이렇게 되는데 상술했듯 π×(원의 반지름)=(반원의 호의 길이)이므로 | 이렇게 되는데 상술했듯 π×(원의 반지름)=(반원의 호의 길이)이므로 | ||
<br> | <br /> | ||
(같은 거):π×1rad=(같은 거):(반원의 중심각의 크기)<br> | (같은 거):π×1rad=(같은 거):(반원의 중심각의 크기)<br /> | ||
가 된다. 서로 같은 것에 대한 비례가 같다는 게 무슨 뜻이겠어? 당연히 그것들도 같다는 뜻이다. | 가 된다. 서로 같은 것에 대한 비례가 같다는 게 무슨 뜻이겠어? 당연히 그것들도 같다는 뜻이다. | ||
결국<br> | 결국<br /> | ||
π×1rad=(반원의 중심각의 크기)<br> | π×1rad=(반원의 중심각의 크기)<br /> | ||
가 되므로<br> | 가 되므로<br /> | ||
'''πrad=180°'''이다. | |||
그리하여 2πrad=360°, πrad/2=90°, πrad/4=45°,....이 된다는 것도 알 수 있다. | |||
이러한 이유로 라디안은 원주율과 합쳐서 각도를 나타낼 때도 있는데 이때 °로 끝나지 않기 때문에 각도가 아니라고 착각을 하기가 쉽다.게다가 상술했듯이 원주율 뒤의 rad를 생략할 때가 많아서 π/2가 90°의 각도라는 것을 모르고 이게 길이인 줄 알고 잘못 계산하는 경우가 있다. 조심하자. | |||
하단의 표는 모두 π 뒤에 원래 곱해져 있던 rad를 생략한 것이다. 따라서 그걸 감안하고 보아야 한다. | |||
{| class="wikitable" | {| class="wikitable" | ||
| 48번째 줄: | 63번째 줄: | ||
| 90° | | 90° | ||
| π/2 | | π/2 | ||
|- | |||
| 135° | |||
| 3π/4 | |||
|- | |- | ||
| 180° | | 180° | ||
| π | | π | ||
|- | |||
| 270° | |||
| 3π/2 | |||
|- | |- | ||
| 360° | | 360° | ||
| 56번째 줄: | 77번째 줄: | ||
|} | |} | ||
부채꼴의 반지름의 길이와 호의 길이가 같을 때, 반지름을 <math>r</math>이라 하면 | |||
: <math>2\pi r : 360^\circ = r:\alpha^\circ</math> | |||
에서 | |||
: <math>\alpha^\circ = \frac{180^\circ}{\pi}</math> | |||
이므로 | |||
: <math>1\operatorname{rad}=\frac{180^\circ}{\pi}</math> | : <math>1\operatorname{rad}=\frac{180^\circ}{\pi}</math> | ||
그런데 [[2015 개정 교육과정]]을 따르는 [[미적분Ⅱ]] [[교과서]]를 검토하면 대부분이 일정한 각의 크기 <math>\frac{180^\circ}{\pi}</math>를 <math>1\operatorname{rad}</math>이라 한다<ref>{{저널 인용|저자=최은아, 강향임|연도=2015|월=9|제목=예비교사의 라디안에 대한 이해|저널=학교수학|권=17|호=2| | 을 얻는다. 그런데 [[2015 개정 교육과정]]을 따르는 [[미적분Ⅱ]] [[교과서]]를 검토하면 대부분이 라디안을 "일정한 각의 크기 <math>\frac{180^\circ}{\pi}</math>를 <math>1\operatorname{rad}</math>이라 한다"라고 정의하고 있는데, 이는 라디안이 새로운 측도가 아니라 단순히 60분법의 변환에 불과하다는 인상을 준다는 단점이 있다.<ref name="choi">{{저널 인용|저자=최은아, 강향임|연도=2015|월=9|제목=예비교사의 라디안에 대한 이해|저널=학교수학|권=17|호=2}}</ref>{{rp|313-314}} | ||
== 호의 길이와 넓이 == | == 호의 길이와 넓이 == | ||
{{ | {{참고|부채꼴}} | ||
반지름이 <math>r</math>, 중심각이 <math>\theta</math>인 부채꼴의 호의 길이를 <math>l</math>, 부채꼴의 넓이를 <math>S</math>라 하면 | 반지름이 <math>r</math>, 중심각이 <math>\theta</math>인 부채꼴의 호의 길이를 <math>l</math>, 부채꼴의 넓이를 <math>S</math>라 하면 | ||
: <math>l=r\theta</math> | : <math>l=r\theta</math> | ||
: <math>S=\frac{1}{2}r^2\theta = \frac{1}{2}rl</math> | : <math>S=\frac{1}{2}r^2\theta = \frac{1}{2}rl</math> | ||
이다. | 이다. | ||
{{글 숨김|제목=Proof | {{글 숨김 시작|제목=Proof}}중심각의 크기에 정비례하기 때문에 | ||
: <math>2\pi r : l = 2\pi : \theta</math> | : <math>2\pi r : l = 2\pi : \theta</math> | ||
이고, 따라서 호의 길이는 | 이고, 따라서 호의 길이는 | ||
| 76번째 줄: | 100번째 줄: | ||
: <math>S=\frac{\pi r^2\theta}{2\pi}=\frac{1}{2}r^2\theta=\frac{1}{2}rl</math> | : <math>S=\frac{\pi r^2\theta}{2\pi}=\frac{1}{2}r^2\theta=\frac{1}{2}rl</math> | ||
이다. | 이다. | ||
}} | {{글 숨김 끝}} | ||
{{글 숨김 시작|제목=말로 풀이}} | |||
우선 부채꼴에서 호의 길이는 중심각의 크기에 비례하기 때문에<br /> | |||
(원의 지름):(부채꼴의 호의 길이)=(원의 중심각의 크기(?)<ref>360° 말하는 거지 뭐겠어?</ref>:(부채꼴의 중심각의 크기)이다. | |||
이때 이 비를 [[비례식]] 문서에도 나오지만 '''분수 형태로 바꿔줄 수 있다.'''<br /> | |||
<math>\frac{(원의 지름)}{(부채꼴의 호의 길이)} = \frac{(원의 중심각의 크기)}{(부채꼴의 중심각의 크기)}</math><br /> | |||
이렇게. | |||
이때 양변에 <math>\frac{(부채꼴의 호의 길이)×(부채꼴의 중심각의 크기)}{(원의 중심각의 크기)}</math>를 곱해주면 양변이 약분이 되면서<br /> | |||
(부채꼴의 호의 길이)=<math>\frac{(원의 지름)×(부채꼴의 중심각의 크기)}{(원의 중심각의 크기)}</math>가 된다. | |||
따라서 위 증명에서 서술했듯 <math>S=\frac{\pi r^2\theta}{2\pi}=\frac{1}{2}r^2\theta=\frac{1}{2}rl</math>가 된다. | |||
Q.E.D. | |||
{{글 숨김 끝}} | |||
여기서 <math>l=r\theta</math>에 등장하는 <math>\theta</math>에는 <math>\operatorname{rad}</math>이 붙어있지 않다. <math>\operatorname{rad}</math>가 붙어 있다고 가정하고, <math>r,l</math>에 길이 단위인 미터를 붙이면 | 여기서 <math>l=r\theta</math>에 등장하는 <math>\theta</math>에는 <math>\operatorname{rad}</math>이 붙어있지 않다. <math>\operatorname{rad}</math>가 붙어 있다고 가정하고, <math>r,l</math>에 길이 단위인 미터를 붙이면 | ||
: <math>l\;(\mathrm{m})=r\theta\;(\mathrm{m\times rad})</math> | : <math>l\;(\mathrm{m})=r\theta\;(\mathrm{m\times rad})</math> | ||
으로 단위 차원이 일치하지 않기 때문이다.<ref>{{저널 인용|저자=김완재|연도=2009|월=8|제목=라디안의 속성에 관한 연구: 1rad은 각인가 실수인가?|저널=수학교육학연구|권=19|호=3|쪽=446}}</ref> | 으로 단위 차원이 일치하지 않기 때문이다.<ref>{{저널 인용|저자=김완재|연도=2009|월=8|제목=라디안의 속성에 관한 연구: 1rad은 각인가 실수인가?|저널=수학교육학연구|권=19|호=3|쪽=446}}</ref> | ||
== 미적분과 라디안 == | |||
: <math>\lim_{x\to 0}\frac{\sin x}{x} =1</math> | |||
: <math>\lim_{x\to 0}\frac{\sin x^\circ}{x}=\frac{\pi}{180}</math> | |||
: <math>\frac{d}{dx}\sin x =\cos x</math> | |||
: <math>\frac{d}{dx}\sin x^\circ = \frac{\pi}{180}\cos x^\circ</math> | |||
: <math>\sin x = x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots</math> | |||
: <math>\sin x = \frac{\pi}{180}x -\left(\frac{\pi}{180}\right)^3\frac{x^3}{3!}+\left(\frac{\pi}{180}\right)^5\frac{x^5}{5!}-\left(\frac{\pi}{180}\right)^7\frac{x^7}{7!}+\cdots</math> | |||
== 물리학과 라디안 == | |||
라디안은 무차원인 [[SI 유도 단위]]이다. 라디안은 교수자와 학습자 모두에게 혼동을 일으킨다.<ref name="aapt">{{저널 인용|저자=The AAPT Metric Education and SI Practices Committee (Gordon J. Aubrecht, Anthony P. French, Mario Iona, and Daniel W. Welch|연도=1993|월=2|제목=The Radian - That Troublesome Unit|저널=The Physics Teacher|권=31}}</ref>{{rp|84}} 예를 들어, 접선 속력 공식을 살펴보자. | |||
: <math>v_t = r\frac{d\theta}{dt}=r\omega</math> | |||
이때 <math>r</math>의 단위를 <math>\mathrm{m}</math>, <math>\omega</math>의 단위를 <math>\operatorname{rad}/\mathrm{s}</math>로 두면 <math>v_t</math>의 단위는 <math>\mathrm{m}\cdot \operatorname{rad}/\mathrm{s}</math>가 되는데, 이는 속력의 단위가 <math>\mathrm{m/s}</math>인 것과 일치하지 않는다.<ref name="aapt" />{{rp|86}} | |||
== 포장함수 == | == 포장함수 == | ||
{{ | {{참고|삼각함수}} | ||
원 <math>x^2+y^2= r^2\;(r>0)</math> 위의 임의의 한 점을 <math>\mathrm{P}(x,y)</math>라 하고, <math>\mathrm{A}=(r,0)</math>이며, <math>\theta=\angle \mathrm{POA}</math>라 하면 삼각함수는 다음과 같이 정의된다. | 원 <math>x^2+y^2= r^2\;(r>0)</math> 위의 임의의 한 점을 <math>\mathrm{P}(x,y)</math>라 하고, <math>\mathrm{A}=(r,0)</math>이며, <math>\theta=\angle \mathrm{POA}</math>라 하면 삼각함수는 다음과 같이 정의된다. | ||
: <math>\sin\theta=\frac{y}{r}</math> | : <math>\sin\theta=\frac{y}{r}</math> | ||
| 89번째 줄: | 148번째 줄: | ||
: <math>\sec\theta=\frac{r}{x}</math> | : <math>\sec\theta=\frac{r}{x}</math> | ||
: <math>\cot\theta=\frac{x}{y}</math> | : <math>\cot\theta=\frac{x}{y}</math> | ||
삼각함수는 실수 집합에서 실수 집합으로 가는 함수가 맞을까? | 이때 삼각함수는 실수 집합에서 실수 집합으로 가는 함수가 맞을까? 어떤 교과서는 "일반각을 호도법으로 나타내고 단위를 생략하면 실수 집합에서 실수 집합으로 가는 함수가 된다"라고 서술하며,<ref>{{서적 인용|제목=미적분Ⅱ 교사용 지도서|저자=우정호 외 24명|연도=2014|출판사=두산동아(주)}}</ref> 예비교사 다수도 <math>\operatorname{rad}</math>를 생략하면 삼각함수의 정의역이 실수가 된다고 답하였다.<ref name="choi" />{{rp|321}} 래핑을 통한 은유가 제안되기도 한다.<ref>{{저널 인용|저자=Hatice Akkoc|연도=2008|월=10|제목=Pre-service mathematics teachers’ concept images of radian|저널=International Journal of Mathematical Education in Science and Technology|권=39|호=7|쪽=876}}</ref> 실제로 Precalculus 교재 일부는 | ||
포장함수(wrapping function) <math>W(x)</math>를 정의한다.<ref>{{서적 인용|제목=Precalculus: Functions and Graphs|저자=Raymond A. Barnett, Michael R. Ziegler, Karl E. Byleen|url=http://www.mhhe.com/math/precalc/barnettpc5/graphics/barnett05pcfg/ch05/others/bpc5_ch05-01.pdf|확인날짜=2016-04-12|판=5th edition|날짜=2000-07-01|출판사=McGraw-Hill Science/Engineering/Math|ISBN=978-0072368710|장=Chapter 5, Section 1}}</ref> | 포장함수(wrapping function) <math>W(x)</math>를 정의한다.<ref>{{서적 인용|제목=Precalculus: Functions and Graphs|저자=Raymond A. Barnett, Michael R. Ziegler, Karl E. Byleen|url=http://www.mhhe.com/math/precalc/barnettpc5/graphics/barnett05pcfg/ch05/others/bpc5_ch05-01.pdf|확인날짜=2016-04-12|판=5th edition|날짜=2000-07-01|출판사=McGraw-Hill Science/Engineering/Math|ISBN=978-0072368710|장=Chapter 5, Section 1}}</ref> | ||
: <math>W(0)=(1,0)</math> | : <math>W(0)=(1,0)</math> | ||
| 98번째 줄: | 157번째 줄: | ||
== 같이 보기 == | == 같이 보기 == | ||
* [[삼각함수]] | * [[삼각함수]] | ||
== 외부 링크 == | |||
* <small>'''(영어)'''</small> [https://www.mathsisfun.com/geometry/radians.html Radians] | |||
{{각주}} | {{각주}} | ||
[[분류:단위]] | |||
[[분류:기하학]] | |||
2022년 8월 13일 (토) 12:06 기준 최신판
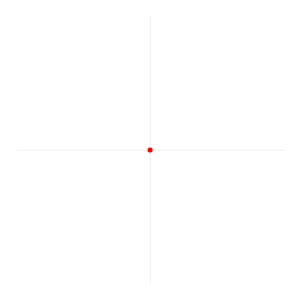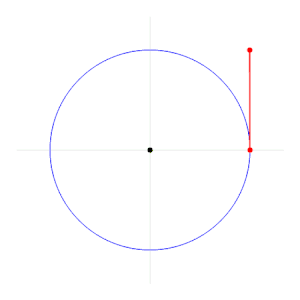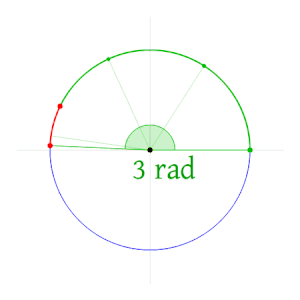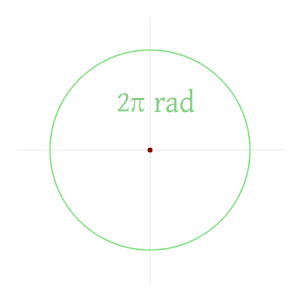
라디안(radian)은 각도 단위 중 하나로, 부채꼴의 반지름과 호의 길이가 같을 때 중심각의 크기를 1라디안이라고 하고, [math]\displaystyle{ 1\operatorname{rad} }[/math]로 쓴다. 보통 [math]\displaystyle{ \operatorname{rad} }[/math]는 생략한다. 예를 들어, [math]\displaystyle{ \sin (1\operatorname{rad}) }[/math]은 [math]\displaystyle{ \sin 1 }[/math]로 간단하게 표기한다.
역사[편집 | 원본 편집]
라디안이라는 표현이 사용된 것은 비교적 최근으로 알려져 있다.
호도, 즉 부채꼴의 반지름의 길이와 호의 길이가 같을 때 그 부채꼴의 중심각의 각도라는 개념 자체는 1917년 영국의 수학자였던 로저 코츠(Roger Cotes, 1682년 7월 10일~1716년 6월 5일)에 의해 이미 사용되고 있었다. 다만 어디까지나 개념만 언급한 것이지, 라디안이라는 이름까진 언급하진 않고 있다.[1]
현재까지 남겨진 기록 중 라디안이라는 이름이 처음으로 등장하기 시작한 것은 1873년 6월 5일 퀸스 대학교 벨파스트의 물리학자였던 제임스 톰슨(James Thomson)이 낸 시험 문제에서의 등장이 처음이라고 한다. 카더라 통신에 의하면 원래 제임스 톰슨이 라디안이라는 표현을 쓴 것은 그보다 훨씬 전인 1871년부터였지만.
세인트앤드루스 대학교의 교수였던 토머스 뮤어는 1869년 내내 '이 부채꼴의 반지름의 길이와 호의 길이가 같을 때 그 부채꼴의 중심각의 각도'의 이름을 라드(rad), 라디알(radial), 라디안(radian) 중에서 뭘로 정할지 고민했었다고 한다.
이후 6년이라는 긴 시간이 지난 1874년이 되어서야 토머스 뮤어는 이 특수한 각의 명칭을 제임스 톰슨과의 상의 끝에 라디안으로 채택하게 된다.[2]
60분법과의 관계[편집 | 원본 편집]
라디안과 60분법의 관계를 알기 위해서는 세 가지를 머릿속에 담고 있어야 한다.
첫번째로, 원주율에 대해서 명심할 사실이 있는데 π×(원의 지름)=(원의 둘레)라는 사실이다. 양변에 똑같이 2를 나눠보면 π×(원의 지름)/2=(원의 둘레)/2가 되므로 π×(원의 반지름)=(반원의 호의 길이)가 된다.
두번째로, 부채꼴에서 중심각의 크기는 그 부채꼴의 호의 길이에 비례한다는 사실이다.
세번째로, 중심각이 1rad인 부채꼴의 호의 길이는 반지름과 같다.이다.
따라서
π×(원의 반지름):π×1rad=(반원의 호의 길이):(반원의 중심각의 크기)
이렇게 되는데 상술했듯 π×(원의 반지름)=(반원의 호의 길이)이므로
(같은 거):π×1rad=(같은 거):(반원의 중심각의 크기)
가 된다. 서로 같은 것에 대한 비례가 같다는 게 무슨 뜻이겠어? 당연히 그것들도 같다는 뜻이다.
결국
π×1rad=(반원의 중심각의 크기)
가 되므로
πrad=180°이다.
그리하여 2πrad=360°, πrad/2=90°, πrad/4=45°,....이 된다는 것도 알 수 있다.
이러한 이유로 라디안은 원주율과 합쳐서 각도를 나타낼 때도 있는데 이때 °로 끝나지 않기 때문에 각도가 아니라고 착각을 하기가 쉽다.게다가 상술했듯이 원주율 뒤의 rad를 생략할 때가 많아서 π/2가 90°의 각도라는 것을 모르고 이게 길이인 줄 알고 잘못 계산하는 경우가 있다. 조심하자.
하단의 표는 모두 π 뒤에 원래 곱해져 있던 rad를 생략한 것이다. 따라서 그걸 감안하고 보아야 한다.
| 도 | 라디안 |
|---|---|
| 0° | 0 |
| 15° | π/12 |
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 90° | π/2 |
| 135° | 3π/4 |
| 180° | π |
| 270° | 3π/2 |
| 360° | 2π |
부채꼴의 반지름의 길이와 호의 길이가 같을 때, 반지름을 [math]\displaystyle{ r }[/math]이라 하면
- [math]\displaystyle{ 2\pi r : 360^\circ = r:\alpha^\circ }[/math]
에서
- [math]\displaystyle{ \alpha^\circ = \frac{180^\circ}{\pi} }[/math]
이므로
- [math]\displaystyle{ 1\operatorname{rad}=\frac{180^\circ}{\pi} }[/math]
을 얻는다. 그런데 2015 개정 교육과정을 따르는 미적분Ⅱ 교과서를 검토하면 대부분이 라디안을 "일정한 각의 크기 [math]\displaystyle{ \frac{180^\circ}{\pi} }[/math]를 [math]\displaystyle{ 1\operatorname{rad} }[/math]이라 한다"라고 정의하고 있는데, 이는 라디안이 새로운 측도가 아니라 단순히 60분법의 변환에 불과하다는 인상을 준다는 단점이 있다.[3]
호의 길이와 넓이[편집 | 원본 편집]
반지름이 [math]\displaystyle{ r }[/math], 중심각이 [math]\displaystyle{ \theta }[/math]인 부채꼴의 호의 길이를 [math]\displaystyle{ l }[/math], 부채꼴의 넓이를 [math]\displaystyle{ S }[/math]라 하면
- [math]\displaystyle{ l=r\theta }[/math]
- [math]\displaystyle{ S=\frac{1}{2}r^2\theta = \frac{1}{2}rl }[/math]
이다.
Proof 중심각의 크기에 정비례하기 때문에
이고, 따라서 호의 길이는
이다. 마찬가지로 부채꼴의 넓이도 중심각의 크기에 정비례하기 때문에
이고, 따라서
이다. |
말로 풀이 우선 부채꼴에서 호의 길이는 중심각의 크기에 비례하기 때문에 이때 이 비를 비례식 문서에도 나오지만 분수 형태로 바꿔줄 수 있다. 이때 양변에 [math]\displaystyle{ \frac{(부채꼴의 호의 길이)×(부채꼴의 중심각의 크기)}{(원의 중심각의 크기)} }[/math]를 곱해주면 양변이 약분이 되면서 따라서 위 증명에서 서술했듯 [math]\displaystyle{ S=\frac{\pi r^2\theta}{2\pi}=\frac{1}{2}r^2\theta=\frac{1}{2}rl }[/math]가 된다. Q.E.D. |
여기서 [math]\displaystyle{ l=r\theta }[/math]에 등장하는 [math]\displaystyle{ \theta }[/math]에는 [math]\displaystyle{ \operatorname{rad} }[/math]이 붙어있지 않다. [math]\displaystyle{ \operatorname{rad} }[/math]가 붙어 있다고 가정하고, [math]\displaystyle{ r,l }[/math]에 길이 단위인 미터를 붙이면
- [math]\displaystyle{ l\;(\mathrm{m})=r\theta\;(\mathrm{m\times rad}) }[/math]
으로 단위 차원이 일치하지 않기 때문이다.[5]
미적분과 라디안[편집 | 원본 편집]
- [math]\displaystyle{ \lim_{x\to 0}\frac{\sin x}{x} =1 }[/math]
- [math]\displaystyle{ \lim_{x\to 0}\frac{\sin x^\circ}{x}=\frac{\pi}{180} }[/math]
- [math]\displaystyle{ \frac{d}{dx}\sin x =\cos x }[/math]
- [math]\displaystyle{ \frac{d}{dx}\sin x^\circ = \frac{\pi}{180}\cos x^\circ }[/math]
- [math]\displaystyle{ \sin x = x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots }[/math]
- [math]\displaystyle{ \sin x = \frac{\pi}{180}x -\left(\frac{\pi}{180}\right)^3\frac{x^3}{3!}+\left(\frac{\pi}{180}\right)^5\frac{x^5}{5!}-\left(\frac{\pi}{180}\right)^7\frac{x^7}{7!}+\cdots }[/math]
물리학과 라디안[편집 | 원본 편집]
라디안은 무차원인 SI 유도 단위이다. 라디안은 교수자와 학습자 모두에게 혼동을 일으킨다.[6] 예를 들어, 접선 속력 공식을 살펴보자.
- [math]\displaystyle{ v_t = r\frac{d\theta}{dt}=r\omega }[/math]
이때 [math]\displaystyle{ r }[/math]의 단위를 [math]\displaystyle{ \mathrm{m} }[/math], [math]\displaystyle{ \omega }[/math]의 단위를 [math]\displaystyle{ \operatorname{rad}/\mathrm{s} }[/math]로 두면 [math]\displaystyle{ v_t }[/math]의 단위는 [math]\displaystyle{ \mathrm{m}\cdot \operatorname{rad}/\mathrm{s} }[/math]가 되는데, 이는 속력의 단위가 [math]\displaystyle{ \mathrm{m/s} }[/math]인 것과 일치하지 않는다.[6]
포장함수[편집 | 원본 편집]
원 [math]\displaystyle{ x^2+y^2= r^2\;(r\gt 0) }[/math] 위의 임의의 한 점을 [math]\displaystyle{ \mathrm{P}(x,y) }[/math]라 하고, [math]\displaystyle{ \mathrm{A}=(r,0) }[/math]이며, [math]\displaystyle{ \theta=\angle \mathrm{POA} }[/math]라 하면 삼각함수는 다음과 같이 정의된다.
- [math]\displaystyle{ \sin\theta=\frac{y}{r} }[/math]
- [math]\displaystyle{ \cos\theta=\frac{x}{r} }[/math]
- [math]\displaystyle{ \tan\theta=\frac{y}{x} }[/math]
- [math]\displaystyle{ \csc\theta=\frac{r}{y} }[/math]
- [math]\displaystyle{ \sec\theta=\frac{r}{x} }[/math]
- [math]\displaystyle{ \cot\theta=\frac{x}{y} }[/math]
이때 삼각함수는 실수 집합에서 실수 집합으로 가는 함수가 맞을까? 어떤 교과서는 "일반각을 호도법으로 나타내고 단위를 생략하면 실수 집합에서 실수 집합으로 가는 함수가 된다"라고 서술하며,[7] 예비교사 다수도 [math]\displaystyle{ \operatorname{rad} }[/math]를 생략하면 삼각함수의 정의역이 실수가 된다고 답하였다.[3] 래핑을 통한 은유가 제안되기도 한다.[8] 실제로 Precalculus 교재 일부는 포장함수(wrapping function) [math]\displaystyle{ W(x) }[/math]를 정의한다.[9]
- [math]\displaystyle{ W(0)=(1,0) }[/math]
- [math]\displaystyle{ W(1)=(0,1) }[/math]
- [math]\displaystyle{ W\left(\frac{3}{4}\pi\right)=\left(-\frac{\sqrt{2}}{2}.\frac{\sqrt{2}}{2}\right) }[/math]
[math]\displaystyle{ \cos\theta }[/math]는 [math]\displaystyle{ W(\theta) }[/math]의 [math]\displaystyle{ x }[/math]좌표, [math]\displaystyle{ \sin\theta }[/math]는 [math]\displaystyle{ W(\theta) }[/math]의 [math]\displaystyle{ y }[/math]좌표로 정의한다.[10]
같이 보기[편집 | 원본 편집]
외부 링크[편집 | 원본 편집]
- (영어) Radians
각주
- ↑ http://www-groups.dcs.st-and.ac.uk/~history/Printonly/Cotes.html
- ↑ 카조리 플로리안, 1929년, History of Mathematical Notations 2. pp.147–148, ISBN 0-486-67766-4.
- ↑ 3.0 3.1 최은아, 강향임 (2015년 9월). 예비교사의 라디안에 대한 이해. 《학교수학》 17 (2).
- ↑ 360° 말하는 거지 뭐겠어?
- ↑ 김완재 (2009년 8월). 라디안의 속성에 관한 연구: 1rad은 각인가 실수인가?. 《수학교육학연구》 19 (3): 446.
- ↑ 6.0 6.1 The AAPT Metric Education and SI Practices Committee (Gordon J. Aubrecht, Anthony P. French, Mario Iona, and Daniel W. Welch (1993년 2월). The Radian - That Troublesome Unit. 《The Physics Teacher》 31.
- ↑ 우정호 외 24명 (2014). 《미적분Ⅱ 교사용 지도서》. 두산동아(주)
- ↑ Hatice Akkoc (2008년 10월). Pre-service mathematics teachers’ concept images of radian. 《International Journal of Mathematical Education in Science and Technology》 39 (7): 876.
- ↑ Raymond A. Barnett, Michael R. Ziegler, Karl E. Byleen (2000년 7월 1일). 〈Chapter 5, Section 1〉, 《Precalculus: Functions and Graphs》, 5th edition, McGraw-Hill Science/Engineering/Math. ISBN 978-0072368710. 2016년 4월 12일에 확인.
- ↑ Raymond A. Barnett, Michael R. Ziegler, Karl E. Byleen (2000년 7월 1일). 〈Chapter 5, Section 2〉, 《Precalculus: Functions and Graphs》, 5th edition, McGraw-Hill Science/Engineering/Math. ISBN 978-0072368710. 2016년 4월 12일에 확인.