카르노의 정리(Carnot's theorem, -定理)는 유클리드 평면 기하학의 정리로, 프랑스의 공학자이자 수학자인 라자르 카르노(Lazare Carnot, 1753년 - 1823년)의 이름이 붙어 있다. 다음과 같이 간단히 공식화할 수 있다.
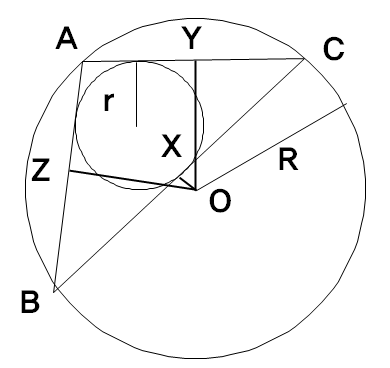
- ABC를 임의의 삼각형이라 하고, O를 이 삼각형에 외접하는 원의 중심이라 하자. 그러면 O에서 AB, BC, CA에 대한 부호거리(signed distances)는 다음을 만족한다.(우측 도해 참조)
- X, Y, Z는 각각 원의 중심 O에서 BC, CA, AB에 내리는 수선의 발이라고 한다.
- [math]\displaystyle{ OX + OY + OZ = R + r,\ }[/math] 여기서 R는 ABC의 외접원의 반지름, r는 ABC의 내접원의 반지름이다.
부호거리가 음수가 되는 경우는 외접원의 중심에서 내린 수선이 ABC의 바깥에만 놓이는 경우이며, ABC의 안팎에 겹치거나 안쪽에만 놓이면 부호거리는 양수가 된다. 카르노의 정리는 일본인의 정리를 증명하는 데도 이용된다.
증명[편집 | 원본 편집]
일단 [math]\displaystyle{ \bar{OX}=R \cos ( \angle A), \bar{OY}=R \cos ( \angle B), \bar{OZ}=R \cos ( \angle C) }[/math]이므로 [1]
[math]\displaystyle{ OX + OY + OZ = R \cos ( \angle A)+\cos ( \angle B)+\cos ( \angle C) }[/math] (1)
한편 삼각형 [math]\displaystyle{ \triangle ABC }[/math]의 넓이는
[math]\displaystyle{ S = 1/2 \times (OX \cdot BC + OY \cdot AC + OZ \cdot AB) }[/math]
사인법칙을 이용하면 다음과 같은 결과를 얻을 수 있다.
[math]\displaystyle{ S = R^2 \times \left( \cos ( \angle A) \sin( \angle A ) + \cos ( \angle B) \sin ( \angle B )+ \cos ( \angle C) \sin ( \angle C) \right) }[/math] (2)
한편 삼각형의 넓이는 내접원의 반지름 r에 대해서 다음과 같은 결과가 나온다.
[math]\displaystyle{ S = 1/2 \times r \times ( AB + BC +CA ) = rR \times ( \sin ( \angle A) + \sin (\angle B) + \sin (\angle C) }[/math] (3)
(3)에서 (2)을 나누면 [math]\displaystyle{ r/R = \frac { \left( \cos ( \angle A) \sin( \angle A ) + \cos ( \angle B) \sin ( \angle B )+ \cos ( \angle C) \sin ( \angle C) \right) }{ \sin (\angle A) + \sin ( \angle B) + \sin ( \angle C) } }[/math] (4)
(4)에서 [math]\displaystyle{ 1 +r/R = \frac { \left( \cos ( \angle A) \sin( \angle A ) + \cos ( \angle B) \sin ( \angle B )+ \cos ( \angle C) \sin ( \angle C) \right) + \sin (\angle A) + \sin ( \angle B) + \sin ( \angle C) }{ \sin (\angle A) + \sin ( \angle B) + \sin ( \angle C) } }[/math] (5)
이제 (5) = [math]\displaystyle{ \cos ( \angle A ) + \cos (\angle B) + \cos (\angle C) }[/math]임을 보이면 된다.
하지만 [math]\displaystyle{ \angle A + \angle B + \angle C = \pi }[/math]이므로 삼각함수의 덧셈정리를 이용하면
[math]\displaystyle{ \begin{align} (& \cos ( \angle A ) + \cos (\angle B) + \cos (\angle C) )( \sin ( \angle A ) + \sin (\angle B) + \sin (\angle C) ) \\ =& \left( \cos ( \angle A) \sin( \angle A ) + \cos ( \angle B) \sin ( \angle B )+ \cos ( \angle C) \sin ( \angle C) \right) \\ +& \left ( \sin (\angle A) \cos ( \angle B) + \cos (\angle A) \sin (\angle B) \right) \\ +& \left ( \sin (\angle A) \cos ( \angle C) + \cos (\angle A) \sin (\angle C) \right) \\ +& \left ( \sin (\angle B) \cos ( \angle C) + \cos (\angle B) \sin (\angle C) \right) \\ =& \left( \cos ( \angle A) \sin( \angle A ) + \cos ( \angle B) \sin ( \angle B )+ \cos ( \angle C) \sin ( \angle C) \right)\\ +& \sin (\angle A) + \sin ( \angle B) + \sin ( \angle C) \end{align} }[/math]
따라서 카르노의 정리가 증명되었다.
관련 문서[편집 | 원본 편집]
외부 링크[편집 | 원본 편집]
각주
- ↑ 삼각형 바깥쪽으로 뻗은 수선의 길이는 음수가 된다.