이등변삼각형이란, 두 변의 길이가 같은 삼각형을 일컫는 말이다. 당연한 소리지만, 이등변삼각형은 수많은 삼각형 중에 한 특별한 경우이다. 그런데, "모든 삼각형이 실은 이등변삼각형이다"임을 보이는 "증명"이 있다면 믿겠는가? 이 유클리드 기하학의 오류는 1892년에 W. W. Rouse Ball에 의해 제기되었다. 먼저 이 잘못된 "증명"을 살펴보자.
진술[편집 | 원본 편집]
- 명제
- 증명?
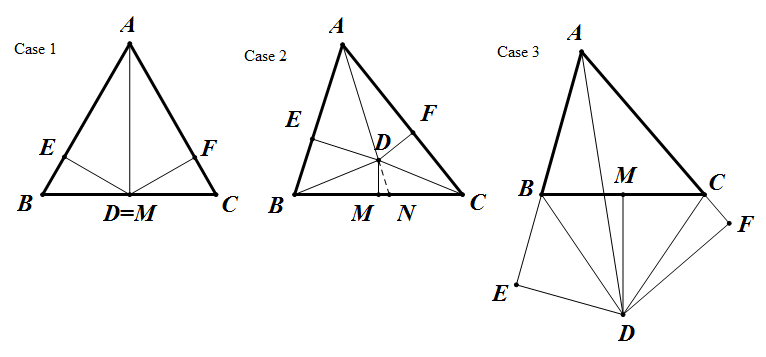
먼저, 변 [math]\displaystyle{ \overline{BC} }[/math]의 중점을 [math]\displaystyle{ M }[/math]이라 하자. 그리고, 각 [math]\displaystyle{ \angle{A} }[/math]의 이등분선과 [math]\displaystyle{ \overline{BC} }[/math]의 수직이등분선이 만나는 교점을 [math]\displaystyle{ D }[/math]이라 하자. 그리고, [math]\displaystyle{ D }[/math]에서 변 [math]\displaystyle{ \overline{AB},\,\overline{AC} }[/math]에 내린 수선의 발을 각각 [math]\displaystyle{ E,\,F }[/math]라고 부르자. 그럼, 점 [math]\displaystyle{ D }[/math]의 위치에 따라 총 세 가지 경우로 나눌 수 있다.
- [math]\displaystyle{ D }[/math]가 변 [math]\displaystyle{ \overline{BC} }[/math]위에 존재하는 경우 (왼쪽 그림)
- [math]\displaystyle{ \angle{EAD}=\angle{FAD} }[/math](각의 이등분선), [math]\displaystyle{ \angle{AED}=\angle{AFD}=90^\circ }[/math], [math]\displaystyle{ \overline{AD} }[/math] 공통이므로, [math]\displaystyle{ \triangle{AED}\cong\triangle{AFD} }[/math](RHA)이다. 따라서, [math]\displaystyle{ \overline{AE}=\overline{AF} }[/math]이고, [math]\displaystyle{ \overline{ED}=\overline{FD} }[/math]. 한편, [math]\displaystyle{ \overline{BD}=\overline{CD} }[/math](수직이등분선)이므로, [math]\displaystyle{ \triangle{EDB}\cong\triangle{FDC} }[/math](RHS)이다. 따라서, [math]\displaystyle{ \overline{EB}=\overline{FC} }[/math]이고, 곧 [math]\displaystyle{ \overline{AB}=\overline{AE}+\overline{EB}=\overline{AF}+\overline{FC}=\overline{AC} }[/math]. 즉, [math]\displaystyle{ \triangle{ABC} }[/math]는 이등변삼각형이다.
- [math]\displaystyle{ D }[/math]가 삼각형 [math]\displaystyle{ \triangle{ABC} }[/math] 안에 존재하는 경우 (가운데 그림)
- 1번 케이스와 동일하게, [math]\displaystyle{ \triangle{ADE}\cong\triangle{ADF} }[/math](RHA)이다. 따라서, [math]\displaystyle{ \overline{AE}=\overline{AF} }[/math]이고, [math]\displaystyle{ \overline{ED}=\overline{FD} }[/math]. 한편, [math]\displaystyle{ \overline{BM}=\overline{CM} }[/math](수직이등분선), [math]\displaystyle{ \angle{DMB}=\angle{DMC}=90^\circ }[/math](수직이등분선), [math]\displaystyle{ \overline{DM} }[/math] 공통이므로, [math]\displaystyle{ \triangle{DMB}\cong\triangle{DMC} }[/math](SAS)이다. 따라서, [math]\displaystyle{ \overline{DB}=\overline{DC} }[/math]. 이는 곧 [math]\displaystyle{ \triangle{DEB}\cong\triangle{DFC} }[/math](RHS)임을 의미하고, 따라서 [math]\displaystyle{ \overline{EB}=\overline{FC} }[/math]이다. 1번 케이스와 마찬가지로, [math]\displaystyle{ \overline{AB}=\overline{AE}+\overline{EB}=\overline{AF}+\overline{FC}=\overline{AC} }[/math]이고, 따라서 [math]\displaystyle{ \triangle{ABC} }[/math]는 이등변삼각형이다.
- [math]\displaystyle{ D }[/math]가 삼각형 [math]\displaystyle{ \triangle{ABC} }[/math] 밖에 존재하는 경우 (오른쪽 그림)
- 1번 케이스와 동일하게, [math]\displaystyle{ \triangle{ADE}\cong\triangle{ADF} }[/math](RHA)이다. 따라서, [math]\displaystyle{ \overline{AE}=\overline{AF} }[/math]이고, [math]\displaystyle{ \overline{ED}=\overline{FD} }[/math]. 한편, 2번 케이스와 동일하게, [math]\displaystyle{ \triangle{DMB}\cong\triangle{DMC} }[/math]이고, 따라서 [math]\displaystyle{ \overline{DB}=\overline{DC} }[/math]. 이는 곧 [math]\displaystyle{ \triangle{DEB}\cong\triangle{DFC} }[/math](RHS)임을 의미하고, 따라서 [math]\displaystyle{ \overline{EB}=\overline{FC} }[/math]이다. 따라서, [math]\displaystyle{ \overline{AB}=\overline{AE}-\overline{EB}=\overline{AF}-\overline{FC}=\overline{AC} }[/math]이고, [math]\displaystyle{ \triangle{ABC} }[/math]는 이등변삼각형이다.
1, 2, 3의 모든 케이스에 대해 [math]\displaystyle{ \triangle{ABC} }[/math]는 이등변삼각형이었으므로, 모든 삼각형은 곧 이등변삼각형이다.
???
오류[편집 | 원본 편집]
당연히 모든 삼각형이 이등변삼각형일리는 절대 없다. 그러면 위 증명에서 도대체 무엇이 잘못된 것일까? 학교에서 평범하게 수학을 배워온 사람이라면 위 증명의 오류를 아마 찾지 못할 것이다. 위 증명의 논리 전개에는 아무런 오류가 없기 때문. 만약 수학적인 감각이 있는 사람이라면, 위 증명이 불완전하다는 사실을 눈치챌 것이다. 3번 케이스에서, [math]\displaystyle{ D }[/math]에서 내린 두 수선의 발이 반드시 삼각형 외부에서 만난다는 보장이 없기 때문. 즉, 3번 케이스는 두 수선의 발이 외부에 존재하는 경우 (케이스 3), 변 위에 존재하는 경우 (케이스 4), 하나는 외부에 다른 하나는 변 위에 존재하는 경우(케이스 5)로 세분화 되어야 한다.
여기까지 생각해냈다면 대단한 것이지만, 아직 문제의 절반 정도밖에 해결하지 못했다. GSP나 지오지브라를 사용해서 직접 그림을 그려보면 알겠지만, 2, 3, 4번 케이스는 아예 존재하지 않는다. 즉, 위 문제에서 잘못된 것은 논리 전개가 아닌, 그림. 여기서는 2, 3번 케이스가 왜 존재하지 않는지 증명해보도록 하자. 증명은 귀류법을 사용한다. 4번 케이스는 3번 케이스와 증명 방법이 비슷하므로 직접 해보자.
- 해법
- 2번 케이스
- [math]\displaystyle{ \overline{AD} }[/math]의 연장선이 [math]\displaystyle{ \overline{BC} }[/math]와 만나는 점을 [math]\displaystyle{ N }[/math]이라 하자. 먼저, [math]\displaystyle{ \triangle{ADE}\cong\triangle{ADF} }[/math]이므로 [math]\displaystyle{ \angle{DAE}=\angle{DAF} }[/math]이다. 그리고 [math]\displaystyle{ \triangle{DBE}\cong\triangle{DCF} }[/math]이므로 [math]\displaystyle{ \angle{DBE}=\angle{DCF} }[/math]이고, [math]\displaystyle{ \triangle{DBM}\cong\triangle{DCM} }[/math]이므로 [math]\displaystyle{ \angle{DBM}=\angle{DCM} }[/math]이다. 한편, 이 6개의 각의 합은 [math]\displaystyle{ \triangle{ABC} }[/math]의 내각의 합과 같으므로, [math]\displaystyle{ 180^\circ }[/math]이다. 따라서, [math]\displaystyle{ \angle{DAE}+\angle{DBE}+\angle{DBM}=90^\circ }[/math]. 이제, [math]\displaystyle{ \triangle{ABN} }[/math]에서, [math]\displaystyle{ \angle{ANB}=90^\circ }[/math]임을 알 수 있다. 그런데, [math]\displaystyle{ \triangle{DMN} }[/math]의 내각의 합이 [math]\displaystyle{ 180^\circ }[/math]을 넘어가게 되고, 이는 평행선 공준에 모순이다. 모순이 되지 않는 방법은 [math]\displaystyle{ M=N }[/math]인 경우, 즉 1번 케이스일 경우밖에 없다. 따라서, 2번 케이스는 존재할 수 없다.
- 3번 케이스
- 먼저, [math]\displaystyle{ \angle{EAD}=\angle{FAD} }[/math](각의 이등분선)이다. 또한, [math]\displaystyle{ \triangle{BMD}\cong\triangle{CMD} }[/math]이므로 [math]\displaystyle{ \angle{BDM}=\angle{CDM} }[/math]이고, [math]\displaystyle{ \triangle{BDE}\cong\triangle{CDF} }[/math]이므로 [math]\displaystyle{ \angle{BDE}=\angle{CDF} }[/math]이다. 즉, [math]\displaystyle{ \angle{EAD}+\angle{BDM}+\angle{BDE}=\angle{FAD}+angle{CDM}+angle{CDF}=x^\circ }[/math]이다. 마지막으로, [math]\displaystyle{ \angle{AED}=\angle{AFD}=90^\circ }[/math]이다. 이제, [math]\displaystyle{ \triangle{AED} }[/math]에서, [math]\displaystyle{ x\gt 90 }[/math](혹은 [math]\displaystyle{ x\lt 90 }[/math])임을 알 수 있다. 반면, [math]\displaystyle{ \triangle{ADF} }[/math]에서는 [math]\displaystyle{ x\lt 90 }[/math](혹은 [math]\displaystyle{ x\gt 90 }[/math])이다. 이는 모순이므로, 3번 케이스는 존재할 수 없다.
- 참고: 1번 케이스는 아무런 오류가 존재하지 않는다. 1번 케이스가 성립한다면 그 삼각형은 이등변삼각형이 맞다.
의의[편집 | 원본 편집]
그림은 유클리드 기하학의 매우 편리한 도구 중 하나이다. 하지만, 그림에 모든 것을 의존했다가는 이러한 오류를 범하고서는 눈치채지 못할 가능성이 존재한다. 그림을 그려서 문제를 풀 때는, 반드시 모든 경우의 수를 생각해 주어야 하고, 각각의 경우가 수학적으로 맞는지 다시 한 번 체크해 주어야 한다. 만약 그렇지 않다면 이 오류처럼 큰 문제를 야기할 수 있음을 알아두자. 아, 물론 그렇다고 해서 수학의 정석처럼 그림 한 점 없이 기하학 문제를 풀라는 소리는 아니다.