도박사의 파산

도박사의 파산(영어: Gambler's ruin)은 유한한 자금을 가진 도박사가 도박을 계속할 경우 파산할 수밖에 없음을 보여주는 문제다. 아래 문제와 풀이를 잘 보고 도박의 늪에 빠지지 않도록 하자.

간단히 요약하자면 '도박'이라는 게임이 성립하기 위한 특성을 조건으로 하여 반복 시행을 거칠수록 도전자가 목표에 닿을 확률은 점점 0에 수렴하게 된다는 것이다. 만일 도박을 할 것이라면 승패에 무관하게 단판으로 끝내는 것이 가장 효율적이라는 뜻이기도 하다.

역사

1656년에 블레즈 파스칼이 피에르 드 페르마에게 다음 문제를 낸 것이 시초라고 한다. 피에르 드 카르카비(Pierre de Carcavi)는 크리스티안 하위헌스에게 보내는 편지에서 문제를 다음과 같이 요약했다.

두 사람이 주사위 세 개를 굴려서 첫 번째 사람은 11을 굴리면 득점하고, 두 번째 사람은 14를 굴리면 득점한다고 하자. 그런데 득점이 누적되는 기존 방식 대신에 상대방의 점수가 0이면 1점을 얻고, 그렇지 않으면 상대방의 점수를 빼도록 하자. 그것은 마치 두 점수가 짝을 지어 서로를 상쇄하여 지고 있는 쪽이 항상 0점인 것처럼 보인다. 12점을 먼저 얻는 사람이 승자가 된다. 그러면 각 참여자가 이길 확률은 얼마일까?

크리스티안 하위헌스는 1657년에 De Ratiociniis in Ludo Aleae라는 책을 출판하면서 이 문제를 다루었다.

문제 5. 사람 A, B는 자금 12를 가지고 시작하여 주사위 세 개를 굴려서 A는 11이 나올 때, B는 14가 나올 때 상대에게서 자금을 1 가져온다. 먼저 전액을 획득하는 사람이 승리한다. 이때 A와 B가 이길 확률의 비는 244,140,625 : 282,429,536,481이다.

문제

사람 [math]\displaystyle{ A,B }[/math]가 각각 자금 [math]\displaystyle{ i, N-i }[/math]를 가지고 있고, 앞면이 나올 확률이 p인 동전을 던져서 앞면이 나오면 A가 B에게 자금 1을 받고, 반대로 뒷면이 나오면 B가 A에게 자금 1을 받는다. 동전 던지기를 반복했을 때 A가 자금 N을 독차지할 확률은 얼마일까?

풀이

A가 자금 N을 독차지하는 사건을 E로 두고, 자금 i를 가지고 있을 때 자금 N을 독차지할 확률을 [math]\displaystyle{ P_i }[/math]라 하자. 그러면

[math]\displaystyle{ P_i=P(E) }[/math]

이고, 첫 번째 게임에서 앞면이 나오는 사건을 F라 하면 전확률의 법칙(law of total probability)에 의해

[math]\displaystyle{ P(E)=P(E|F)P(F)+P(E|F^c)P(F^c) }[/math]

이다. 만약 F가 발생하면 A는 자금 [math]\displaystyle{ i+1 }[/math]을 가지고, 반대로 [math]\displaystyle{ F^c }[/math]가 발생하면 A는 자금 [math]\displaystyle{ i-1 }[/math]을 가진다. 따라서

[math]\displaystyle{ P(E|F)=P_{i+1} }[/math]

[math]\displaystyle{ P(E|F^c)=P_{i-1} }[/math]

이다. 따라서

[math]\displaystyle{ P_i=pP_{i+1}+(1-p)P_{i-1} }[/math]

이다. 그러면

[math]\displaystyle{ pP_i+(1-p)P_i=pP_{i+1}+(1-p)P_{i-1} }[/math]

이므로

[math]\displaystyle{ P_{i+1}-P_i=\frac{1-p}{p}(P_i-P_{i-1}) }[/math]

이다. 그러면

[math]\displaystyle{ \begin{align} P_2-P_1&=\frac{1-p}{p}(P_1-P_0)\\ P_3-P_2&=\left(\frac{1-p}{p}\right)^2(P_1-P_0)\\ &\vdots\\ P_i-P_{i-1}&=\left(\frac{1-p}{p}\right)^{i-1}(P_1-P_0) \end{align} }[/math]

이고 [math]\displaystyle{ P_0=0 }[/math]이므로 양변을 더하면

[math]\displaystyle{ P_i=\left(1+\frac{1-p}{p}+\left(\frac{1-p}{p}\right)^2+\cdots+\left(\frac{1-p}{p}\right)^{i-1}\right)P_1 }[/math]

이므로 등비수열의 합의 공식에 의해

[math]\displaystyle{ P_i=\begin{cases} \frac{1-\left(\frac{1-p}{p}\right)^i}{1-\frac{1-p}{p}}P_1,&p\ne\frac{1}{2}\\ iP_1,&p=\frac{1}{2} \end{cases} }[/math]

이다. 한편 [math]\displaystyle{ P_N=1 }[/math]이므로

[math]\displaystyle{ P_N=\begin{cases} \frac{1-\left(\frac{1-p}{p}\right)^N}{1-\frac{1-p}{p}}P_1,&p\ne\frac{1}{2}\\ NP_1,&p=\frac{1}{2} \end{cases} }[/math]

에서

[math]\displaystyle{ P_1=\begin{cases} \frac{1-\frac{1-p}{p}}{1-\left(\frac{1-p}{p}\right)^N},&p\ne\frac{1}{2}\\ \frac{1}{N},&p=\frac{1}{2} \end{cases} }[/math]

을 얻는다. 따라서

[math]\displaystyle{ P_i=\begin{cases} \frac{1-\left(\frac{1-p}{p}\right)^i}{1-\left(\frac{1-p}{p}\right)^N},&p\ne\frac{1}{2}\\ \frac{i}{N},&p=\frac{1}{2} \end{cases} }[/math]

을 얻는다.

한편 [math]\displaystyle{ Q_i }[/math]을 B가 자금 [math]\displaystyle{ N-i }[/math]를 가지고 있을 때 자금 N을 독차지할 확률이라 하면

[math]\displaystyle{ Q_i=\begin{cases} \frac{1-\left(\frac{p}{1-p}\right)^i}{1-\left(\frac{p}{1-p}\right)^N},&p\ne\frac{1}{2}\\ \frac{N-i}{N},&p=\frac{1}{2} \end{cases} }[/math]

이다. 그러면

[math]\displaystyle{ P_i+Q_i=1 }[/math]

이므로 A, B 중 하나는 반드시 파산함을 안다.

도박사가 카지노에서 도박을 한다고 가정하자. 그러면 카지노는 자금을 많이 가지고 있으므로 [math]\displaystyle{ N\to\infty }[/math]라고 가정할 수 있다. 만약 [math]\displaystyle{ p\lt \frac{1}{2} }[/math]라면, [math]\displaystyle{ \frac{1-p}{p}\gt 1 }[/math]이므로 [math]\displaystyle{ N\to\infty }[/math]일 때 [math]\displaystyle{ P_i\to 0 }[/math]이다. 즉 A는 파산할 것이 확실하다. 심지어 [math]\displaystyle{ p=\frac{1}{2} }[/math]일 때도 파산하는 건 기정사실인데, 왜냐 하면 [math]\displaystyle{ N\to\infty }[/math]이면 [math]\displaystyle{ \frac{i}{N}\to 0 }[/math]이기 때문이다. 그나마 [math]\displaystyle{ p\gt \frac{1}{2} }[/math]일 때 [math]\displaystyle{ P_i }[/math]는 0이 아닌 유한한 값으로 수렴한다. 그러나 이런 게임을 카지노가 마련해둘 리는 없다.

전략 세우기

[math]\displaystyle{ p=0.48 }[/math]이고 도박사가 100만 원을 가지고 500만 원을 따려고 할 때, 판돈에 따라 도박사가 승리할 확률을 나타낸 그래프

판돈	i	N	승리 확률
1만 원	100	500	1.245×10-14
2만 원	50	250	1.095×10-7
4만 원	25	125	2.889×10-4
10만 원	10	50	0.023
20만 원	5	25	0.077
50만 원	2	10	0.142
100만 원	1	5	0.169

위에서 도박은 파멸을 불러올 뿐이라고 설명했음에도 불구하고 기어이 도박의 늪에 빠졌다면 장기를 최대한 덜 털릴 방법을 찾아보도록 하자. 이제 당신이 100만 원을 가지고 있다고 가정하자. 먼저 돈을 계속 딸 수 있다는 환상 따위는 집어치워야 한다. 어느 정도 돈을 따면 당장 자리에서 일어나도록 하자. 대개의 경우 도박사가 도박에서 이길 확률은 1/2보다 약간 낮거나 같다. 앞에서

[math]\displaystyle{ P_i=\begin{cases} \frac{1-\left(\frac{1-p}{p}\right)^i}{1-\left(\frac{1-p}{p}\right)^N},&p\ne\frac{1}{2}\\ \frac{i}{N},&p=\frac{1}{2} \end{cases} }[/math]

임을 보였다. 만약 [math]\displaystyle{ p\le\frac{1}{2} }[/math]이면, [math]\displaystyle{ P_i }[/math]는 N에 대한 감소함수이다. 즉 게임을 질질 끄는 것은 도박사에게 별로 좋지 않다는 것이다.

당신이 500만 원을 따려고 한다고 하자. 그럼 상대는 400만 원을 가지고 있다고 가정할 수 있다. 각 게임마다 당신이 이길 확률이 [math]\displaystyle{ p=0.48 }[/math]이라고 가정하자.

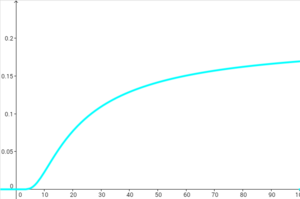
오른쪽 표를 보면 한번에 많은 돈을 걸수록 도박사에게 유리해짐을 알 수 있다. 실제로

[math]\displaystyle{ f(x)=\frac{1-\left(\frac{13}{12}\right)^{\frac{100}{x}}}{1-\left(\frac{13}{12}\right)^{\frac{500}{x}}}\quad(0\lt x\le 100) }[/math]

의 그래프를 그리면 증가함수가 됨을 알 수 있다. 물론 그래봤자 확률의 최댓값이 0.2를 넘지 않으니 그저 눈물이 앞을 가릴 뿐이다.

게임 지속시간

여기서는 도박사가 돈을 딸 수 있을 거라는 환상이 얼마나 지속될 수 있는지 예측하려고 한다. i의 자금을 가지고 있을 때 게임의 평균 지속시간을 [math]\displaystyle{ T_i }[/math]라고 하자. 물론 [math]\displaystyle{ T_i\lt \infty }[/math]인데, 앞에서 자신과 상대 중 한 명은 반드시 돈이 다 털린다는 것을 알았기 때문이다. 이때 첫 판에서 성공했을 때는 [math]\displaystyle{ i+1 }[/math]의 자금을 가지고 시작할 때와 같고 이때 기대시간은 [math]\displaystyle{ T_{i+1}+1 }[/math], 반대로 실패했을 때는 [math]\displaystyle{ i-1 }[/math]의 자금을 가지고 시작할 때와 같고 이때 기대시간은 [math]\displaystyle{ T_{i-1}+1 }[/math]이다. 따라서

[math]\displaystyle{ T_i=pT_{i+1}+(1-p)T_{i-1}+1,\quad 0\lt i\lt N }[/math]

[math]\displaystyle{ T_0=T_N=0 }[/math]

이다. [math]\displaystyle{ p\ne\frac{1}{2} }[/math]일 때,

[math]\displaystyle{ p\left(T_{i+1}-T_i-\frac{1}{1-2p}\right)=(1-p)\left(T_i-T_{i-1}-\frac{1}{1-2p}\right) }[/math]

이므로

[math]\displaystyle{ \begin{align} T_2-T_1-\frac{1}{1-2p}&=\frac{1-p}{p}\left(T_1-T_0-\frac{1}{1-2p}\right)\\ T_3-T_2-\frac{1}{1-2p}&=\left(\frac{1-p}{p}\right)^2\left(T_1-T_0-\frac{1}{1-2p}\right)\\ &\vdots\\ T_i-T_{i-1}-\frac{1}{1-2p}&=\left(\frac{1-p}{p}\right)^{i-1}\left(T_1-T_0-\frac{1}{1-2p}\right) \end{align} }[/math]

이고 [math]\displaystyle{ T_0=0 }[/math]이므로 양변을 모두 더하면

[math]\displaystyle{ \begin{align} T_i-\frac{i}{1-2p}&=\left(1+\frac{1-p}{p}+\left(\frac{1-p}{p}\right)^2+\cdots+\left(\frac{1-p}{p}\right)^{i-1}\right)\left(T_1-\frac{1}{1-2p}\right)\\ &=\frac{1-\left(\frac{1-p}{p}\right)^i}{1-\frac{1-p}{p}}\left(T_1-\frac{1}{1-2p}\right) \end{align} }[/math]

이고 [math]\displaystyle{ T_N=0 }[/math]이므로

[math]\displaystyle{ T_N=\frac{1-\left(\frac{1-p}{p}\right)^N}{1-\frac{1-p}{p}}\left(T_1-\frac{1}{1-2p}\right)+\frac{N}{1-2p}=0 }[/math]

이고, 방정식을 풀면

[math]\displaystyle{ T_1-\frac{1}{1-2p}=-\frac{N}{1-2p}\frac{1-\frac{1-p}{p}}{1-\left(\frac{1-p}{p}\right)^N} }[/math]

이다. 따라서

[math]\displaystyle{ T_i=\frac{i}{1-2p}-\frac{N}{1-2p}\frac{1-\left(\frac{1-p}{p}\right)^i}{1-\left(\frac{1-p}{p}\right)^N} }[/math]

을 얻는다. [math]\displaystyle{ p=\frac{1}{2} }[/math]일 때,

[math]\displaystyle{ T_i=\frac{1}{2}T_{i+1}+\frac{1}{2}T_{i-1}+1 }[/math]

이므로

[math]\displaystyle{ T_{i+1}-T_i=T_i-T_{i-1}-2 }[/math]

이다. 따라서 수열 [math]\displaystyle{ (T_{i}-T_{i-1})_{i=1}^N }[/math]은 공차 -2인 등차수열이다. [math]\displaystyle{ T_0=0 }[/math]이므로,

[math]\displaystyle{ \begin{align} T_1-T_0&=T_1\\ T_2-T_1&=T_1-2\\ T_3-T_2&=T_1-4\\ &\vdots\\ T_{i}-T_{i-1}&=T_1-2(i-1) \end{align} }[/math]

이다. 따라서

[math]\displaystyle{ T_i=iT_1-i(i-1) }[/math]

이고 [math]\displaystyle{ T_N=0 }[/math]이므로

[math]\displaystyle{ T_N=NT_1-N(N-1)=0 }[/math]

이다. 식을 풀면

[math]\displaystyle{ T_1=N-1 }[/math]

를 얻는다. 따라서

[math]\displaystyle{ T_i=i(N-i) }[/math]

이다.

외부 링크

• Steven R. Dunbar (2013). Ruin Probabilities. 2015년 7월 8일에 확인.
• Luc Rey-Bellet. Week 4: Gambler’s ruin and bold play. 2015년 7월 8일에 확인.

같이 보기

• 몬티 홀 게임
• 임의보행