잔글 (→한꼴사상) |
잔글 (→성질) |
||
| 16번째 줄: | 16번째 줄: | ||
=== 성질 === | === 성질 === | ||
([[도함수]]가 [[영점]]을 갖지 않는<ref>도함수가 | ([[도함수]]가 [[영점]]을 갖지 않는<ref>도함수가 0인 점에서는 접선을 그을 수 없고, 즉 각을 정의할 수 없다.</ref>) [[복소]][[정칙사상]]([[해석함수]])은 한꼴사상이다. | ||
''증명''. <br/> | |||
실수 <math>t\in [a,b]</math>로 [[매개화]]된 [[미분가능]]한 곡선 <math>\Gamma(t)</math>와 <math>t_0 \in [a,b]</math>를 생각하자. 정칙사상 <math>f</math>는 <math>\Gamma(t)</math>를 <math>f(\Gamma(t))</math>로 옮길 것이며, <math>z_0=\Gamma(t_0)</math>에서의 편각 <math>theta_0 = \operatorname{arg }\Gamma '(t_0)</math>은 <math>\operatorname{arg }\left ( f'(z_0)\Gamma'(t_0) \right ) = \operatorname{arg }f'(z_0)+ \operatorname{arg } \Gamma' (t_0) = \operatorname{arg }f'(z_0) + \theta_0</math>로 옮겨진다. 즉 <math>z_0</math>를 지나는 두 곡선이 이루는 각은 <math>\operatorname{arg }f'(z_0)</math>만큼만 더해질 뿐 그 크기와 방향은 변하지 않는다. □ | 실수 <math>t\in [a,b]</math>로 [[매개화]]된 [[미분가능]]한 곡선 <math>\Gamma(t)</math>와 <math>t_0 \in [a,b]</math>를 생각하자. 정칙사상 <math>f</math>는 <math>\Gamma(t)</math>를 <math>f(\Gamma(t))</math>로 옮길 것이며, <math>z_0=\Gamma(t_0)</math>에서의 편각 <math>theta_0 = \operatorname{arg }\Gamma '(t_0)</math>은 <math>\operatorname{arg }\left ( f'(z_0)\Gamma'(t_0) \right ) = \operatorname{arg }f'(z_0)+ \operatorname{arg } \Gamma' (t_0) = \operatorname{arg }f'(z_0) + \theta_0</math>로 옮겨진다. 즉 <math>z_0</math>를 지나는 두 곡선이 이루는 각은 <math>\operatorname{arg }f'(z_0)</math>만큼만 더해질 뿐 그 크기와 방향은 변하지 않는다. □ | ||
==== 단락 1.1.1 ==== | ==== 단락 1.1.1 ==== | ||
=== 단락 1.2 === | === 단락 1.2 === | ||
2015년 7월 4일 (토) 19:54 판
한꼴사상
틀:학술 틀:토막글 한꼴사상(conformal mapping, angle-preserving mapping)은 (국소적) 각을 보존하는 사상이다. 보통 복소해석학에서 복소평면 상에서 정의되나, 일반적으로는 더 고차원의 유클리드 공간이나 (준-)리만 다양체에서까지 정의될 수 있다. 이름이 angle-preserving이라 각의 크기만 보존하는 것으로 오해하는 경우가 많은데, 한꼴사상(conformal)은 등각사상(isogonal)과 다르게 각도의 방향(orientation)까지 고려한다. 이름에서 알 수 있듯이, 변환을 해도 전과 같은 한꼴이어야 한다.
복소해석학
열린 [math]\displaystyle{ \Bbb C }[/math]의 부분집합 [math]\displaystyle{ U }[/math]에 대하여, [math]\displaystyle{ f:U\to\Bbb C }[/math]와 [math]\displaystyle{ u\in U }[/math]을 지나는 곡선 [math]\displaystyle{ \Gamma_1 , \Gamma_2 }[/math]을 생각하자. 이때 [math]\displaystyle{ \Gamma_1 , \Gamma_2 }[/math]가 [math]\displaystyle{ u }[/math]에서 이루는 각의 크기와 [math]\displaystyle{ f(\Gamma_1) , f(\Gamma_2) }[/math]가 [math]\displaystyle{ f(u) }[/math]에서 이루는 각[1]이 같다면 이때 [math]\displaystyle{ f }[/math]를 한꼴사상이라 한다.
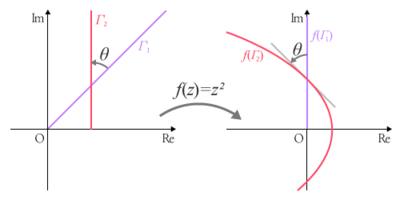
한꼴사상이 곡선의 곡률까지 보존할 필요는 없다. 쉬운 예로, [math]\displaystyle{ f:z \mapsto z^2 }[/math]과 [math]\displaystyle{ \Gamma_1: z=(1+i)t, \; \Gamma_2: z=1+it \; \; (t \in \Bbb R^+) }[/math]을 생각하자. 이 두 곡선은 [math]\displaystyle{ z=1+i \text{ as } t=1 }[/math]에서의 각을 보존([math]\displaystyle{ \theta = 1/4 }[/math])하지만, 곡률은 바뀐다.
성질
(도함수가 영점을 갖지 않는[2]) 복소정칙사상(해석함수)은 한꼴사상이다.
증명.
실수 [math]\displaystyle{ t\in [a,b] }[/math]로 매개화된 미분가능한 곡선 [math]\displaystyle{ \Gamma(t) }[/math]와 [math]\displaystyle{ t_0 \in [a,b] }[/math]를 생각하자. 정칙사상 [math]\displaystyle{ f }[/math]는 [math]\displaystyle{ \Gamma(t) }[/math]를 [math]\displaystyle{ f(\Gamma(t)) }[/math]로 옮길 것이며, [math]\displaystyle{ z_0=\Gamma(t_0) }[/math]에서의 편각 [math]\displaystyle{ theta_0 = \operatorname{arg }\Gamma '(t_0) }[/math]은 [math]\displaystyle{ \operatorname{arg }\left ( f'(z_0)\Gamma'(t_0) \right ) = \operatorname{arg }f'(z_0)+ \operatorname{arg } \Gamma' (t_0) = \operatorname{arg }f'(z_0) + \theta_0 }[/math]로 옮겨진다. 즉 [math]\displaystyle{ z_0 }[/math]를 지나는 두 곡선이 이루는 각은 [math]\displaystyle{ \operatorname{arg }f'(z_0) }[/math]만큼만 더해질 뿐 그 크기와 방향은 변하지 않는다. □
단락 1.1.1
단락 1.2
단락 2
인터위키 테스트
사영기하학
사영기하학(射影幾何學, projective geometry)은 사영변환에 대해 보존되는 성질을 연구하는 매우 추상적인 기하학이다.
뉴턴의 운동 법칙
뉴턴의 운동 법칙(Newton's laws of motion)은 아이작 뉴턴에 의해 정립된 세 가지 물리 법칙이다.
역사
제1 법칙: 관성의 법칙
외력이 없을 때 어떤 물체의 질량중심은 일정한 속도 (또는 운동량)을 가지고 운동한다.
관성의 법칙을 만족하는 기준틀(좌표계)를 관성기준틀(관성좌표계, 관성계)라 부르고, 즉 이는 등속도 운동을 하는 기준틀을 말한다.