한꼴사상(conformal mapping, angle-preserving mapping)은 (국소적으로) 각을 보존하는 사상이다. 보통 복소해석학에서 복소평면 상에서 정의되나, 일반적으로는 더 고차원의 유클리드 공간이나 (준-)리만 다양체에서까지 정의될 수 있다. 이름이 angle-preserving이라 각의 크기만 보존하는 것으로 오해하는 경우가 많은데, 한꼴사상(conformal)은 등각사상(isogonal)과 다르게 각도의 방향(orientation)까지 고려한다. 이름에서 알 수 있듯이, 변환을 해도 전과 같은 한꼴이어야 한다.
복소해석학[편집 | 원본 편집]
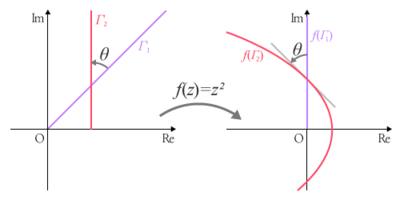
열린 [math]\displaystyle{ \Bbb C }[/math]의 부분집합 [math]\displaystyle{ U }[/math]에 대하여, [math]\displaystyle{ f:U\to\Bbb C }[/math]와 [math]\displaystyle{ u\in U }[/math]을 지나는 곡선 [math]\displaystyle{ \Gamma_1 , \Gamma_2 }[/math]을 생각하자. 이때 [math]\displaystyle{ \Gamma_1 , \Gamma_2 }[/math]가 [math]\displaystyle{ u }[/math]에서 이루는 각의 크기와 [math]\displaystyle{ f(\Gamma_1) , f(\Gamma_2) }[/math]가 [math]\displaystyle{ f(u) }[/math]에서 이루는 각[1]이 같다면 이때 [math]\displaystyle{ f }[/math]를 한꼴사상이라 한다.
한꼴사상이 곡선의 곡률까지 보존할 필요는 없다. 쉬운 예로, [math]\displaystyle{ f:z \mapsto z^2 }[/math]과 [math]\displaystyle{ \Gamma_1: z=(1+i)t, \; \Gamma_2: z=1+it \; \; (t \in \Bbb R^+) }[/math]을 생각하자. 이 두 곡선은 [math]\displaystyle{ z=1+i \text{ as } t=1 }[/math]에서의 각([math]\displaystyle{ \theta_{1,2} = +1/4 }[/math])을 보존하지만, 곡률은 바뀐다.
성질[편집 | 원본 편집]
증명.
실수 [math]\displaystyle{ t\in [a,b] }[/math]로 매개화된 미분가능한 곡선 [math]\displaystyle{ \Gamma(t) }[/math]와 [math]\displaystyle{ t_0 \in [a,b] }[/math]를 생각하자. 정칙사상 [math]\displaystyle{ f }[/math]는 [math]\displaystyle{ \Gamma(t) }[/math]를 [math]\displaystyle{ f(\Gamma(t)) }[/math]로 옮길 것이며, [math]\displaystyle{ z_0=\Gamma(t_0) }[/math]에서의 편각 [math]\displaystyle{ \theta_0 = \operatorname{arg }\Gamma '(t_0) }[/math]은 [math]\displaystyle{ \operatorname{arg }\left ( f'(z_0)\Gamma'(t_0) \right ) = \operatorname{arg }f'(z_0)+ \operatorname{arg } \Gamma' (t_0) = \operatorname{arg }f'(z_0) + \theta_0 }[/math]로 옮겨진다. 즉 [math]\displaystyle{ z_0 }[/math]를 지나는 두 곡선이 이루는 각은 [math]\displaystyle{ \operatorname{arg }f'(z_0) }[/math]만큼만 더해질 뿐 그 크기와 방향은 변하지 않는다. □
다른 정의[편집 | 원본 편집]
한꼴사상에 대한 위와 동치가 아닌 다른 정의가 있다. [math]\displaystyle{ f \quad (\operatorname{dom} f : \text{ open}) }[/math]가 한꼴사상이라는 것은 [math]\displaystyle{ f }[/math]가 단사인 정칙사상임을 말한다. 열린 사상 정리에 의하여, [math]\displaystyle{ f }[/math]의 역사상은 정칙이며, 즉 [math]\displaystyle{ f }[/math]가 단사인 정칙사상임과 biholomolphic임은 동치이다.
이는 1.1의 정의와는 차이가 있는데, 1.1.2의 정의가 1.1의 것의 특수한 경우이다. 단사이며 정칙임은 영점이 없는 도함수를 가짐을 말하지만, 그 역은 성립하지 않는다. (예시로 지수함수가 있다. 이는 정의역이 [math]\displaystyle{ \Bbb C }[/math]의 부분집합일 때 주기성을 가지므로 단사가 아닐 수 있다.)