잔글 (문자열 찾아 바꾸기 - "{{학술 관련 정보}}" 문자열을 "" 문자열로) |
잔글편집 요약 없음 |
||
| (같은 사용자의 중간 판 하나는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
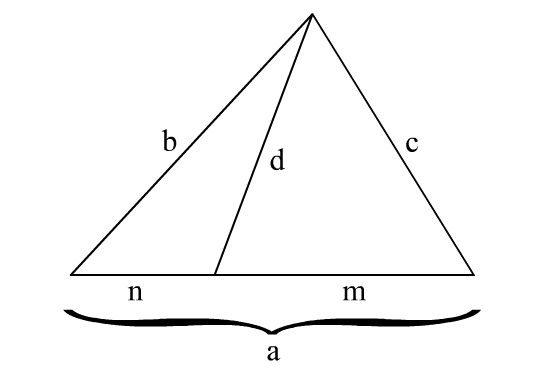
'''스튜어트의 정리'''(Stewarts Theorem)는 스코틀랜드의 수학자 매튜 스튜어트가 증명한 [[정리]]로, [[삼각형]] 관련 문제를 풀 때 아주 유용한 정리이다. [[대한민국]]의 수학 교육과정에선 가르치지 않지만, 중학교 때 경시대회를 준비하거나, 아니면 수학에 따로 관심이 있다면 한 번쯤은 보게 되는 정리 중 하나이다. 자세한 내용은 다음과 같다. | |||
Stewarts Theorem | |||
스코틀랜드의 수학자 매튜 스튜어트가 증명한 | |||
[[파일:스튜어트의 정리 1.png]] | [[파일:스튜어트의 정리 1.png]] | ||
| 20번째 줄: | 16번째 줄: | ||
<math>\overline{AH}=h,\overline{DH}=x</math>라 하자. 그럼 <math>\triangle{ADH}</math>에서 피타고라스 정리에 의해, <math>h^2+x^2=d^2</math>. <math>\triangle{AHB}</math>에서 마찬가지로 <math>h^2+\left(m-x\right)^2=c^2</math>, <math>h^2+m^2-2mx+x^2=d^2+m^2-2mx=c^2</math>이다. 그리고 <math>\triangle{AHC}</math>에서 마찬가지로 <math>h^2+\left(n+x\right)^2=b^2</math>, <math>h^2+n^2+2nx+x^2=d^2+n^2+2nx=b^2</math>이다. 두번째 식에 <math>n</math>을, 세번째 식에 <math>m</math>을 곱하여 더해주면, <math>nd^2+m^2n-2mnx+md^2+mn^2+2mnx=d^2\left(m+n\right)+mn\left(m+n\right)=\left(m+n\right)\left(mn+d^2\right)=a\left(mn+d^2\right)=mb^2+nc^2</math>. | <math>\overline{AH}=h,\overline{DH}=x</math>라 하자. 그럼 <math>\triangle{ADH}</math>에서 피타고라스 정리에 의해, <math>h^2+x^2=d^2</math>. <math>\triangle{AHB}</math>에서 마찬가지로 <math>h^2+\left(m-x\right)^2=c^2</math>, <math>h^2+m^2-2mx+x^2=d^2+m^2-2mx=c^2</math>이다. 그리고 <math>\triangle{AHC}</math>에서 마찬가지로 <math>h^2+\left(n+x\right)^2=b^2</math>, <math>h^2+n^2+2nx+x^2=d^2+n^2+2nx=b^2</math>이다. 두번째 식에 <math>n</math>을, 세번째 식에 <math>m</math>을 곱하여 더해주면, <math>nd^2+m^2n-2mnx+md^2+mn^2+2mnx=d^2\left(m+n\right)+mn\left(m+n\right)=\left(m+n\right)\left(mn+d^2\right)=a\left(mn+d^2\right)=mb^2+nc^2</math>. | ||
== 같이 보기 == | |||
== | |||
* [[피타고라스의 정리]] | * [[피타고라스의 정리]] | ||
{{각주}} | |||
[[분류:기하학]] | [[분류:기하학]] | ||
[[분류:수학 정리]] | |||
2018년 2월 24일 (토) 19:39 기준 최신판
스튜어트의 정리(Stewarts Theorem)는 스코틀랜드의 수학자 매튜 스튜어트가 증명한 정리로, 삼각형 관련 문제를 풀 때 아주 유용한 정리이다. 대한민국의 수학 교육과정에선 가르치지 않지만, 중학교 때 경시대회를 준비하거나, 아니면 수학에 따로 관심이 있다면 한 번쯤은 보게 되는 정리 중 하나이다. 자세한 내용은 다음과 같다.
“ [math]\displaystyle{ mb^2+nc^2=\left(m+n\right)\left(mn+d^2\right)=a\left(mn+d^2\right) }[/math] “
혹시 눈치챈 사람이 있을진 모르지만, 파푸스의 중선 정리의 일반화된 버전이다. 저기서 만약 [math]\displaystyle{ m=n }[/math]이면, [math]\displaystyle{ mb^2+mc^2=2m\left(m^2+d^2\right) }[/math]이고, 양변을 [math]\displaystyle{ m }[/math]로 나눠주면 [math]\displaystyle{ b^2+c^2=2\left(m^2+d^2\right) }[/math]이 되어 보통 고등학교 때 배우는 파푸스의 중선 정리가 된다.
증명[편집 | 원본 편집]
코사인 법칙[편집 | 원본 편집]
두 변 [math]\displaystyle{ m }[/math]과 [math]\displaystyle{ d }[/math]가 이루는 각을 [math]\displaystyle{ \theta }[/math]라 하자. 그럼 오른쪽 삼각형에서 코사인 법칙에 의해, [math]\displaystyle{ c^2=m^2+d^2-2md\cos\theta }[/math]. 왼쪽 삼각형에서 코사인 법칙에 의해, [math]\displaystyle{ b^2=n^2+d^2-2nd\cos\left(\pi-\theta\right)=n^2+d^2+2nd\cos\theta }[/math]. 첫번째 식에 [math]\displaystyle{ n }[/math]을, 두번째 식에 [math]\displaystyle{ m }[/math]을 곱하여 더해주면, [math]\displaystyle{ mb^2+nc^2=m^2n+nd^2-2mnd\cos\theta+mn^2+md^2+2mnd\cos\theta= }[/math] [math]\displaystyle{ m^2n+mn^2+md^2+nd^2=mn\left(m+n\right)+d^2\left(m+n\right)=\left(m+n\right)\left(mn+d^2\right)=a\left(mn+d^2\right) }[/math].
피타고라스 정리[편집 | 원본 편집]
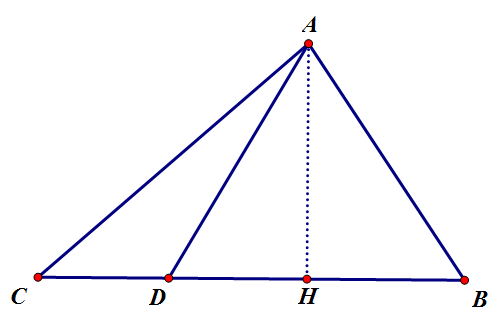
꼭짓점 [math]\displaystyle{ A }[/math]에서 대변에 수선을 내린뒤, 삼각형 3개에 대해 피타고라스 정리를 사용하여 정리해주면 된다.
[math]\displaystyle{ \overline{AH}=h,\overline{DH}=x }[/math]라 하자. 그럼 [math]\displaystyle{ \triangle{ADH} }[/math]에서 피타고라스 정리에 의해, [math]\displaystyle{ h^2+x^2=d^2 }[/math]. [math]\displaystyle{ \triangle{AHB} }[/math]에서 마찬가지로 [math]\displaystyle{ h^2+\left(m-x\right)^2=c^2 }[/math], [math]\displaystyle{ h^2+m^2-2mx+x^2=d^2+m^2-2mx=c^2 }[/math]이다. 그리고 [math]\displaystyle{ \triangle{AHC} }[/math]에서 마찬가지로 [math]\displaystyle{ h^2+\left(n+x\right)^2=b^2 }[/math], [math]\displaystyle{ h^2+n^2+2nx+x^2=d^2+n^2+2nx=b^2 }[/math]이다. 두번째 식에 [math]\displaystyle{ n }[/math]을, 세번째 식에 [math]\displaystyle{ m }[/math]을 곱하여 더해주면, [math]\displaystyle{ nd^2+m^2n-2mnx+md^2+mn^2+2mnx=d^2\left(m+n\right)+mn\left(m+n\right)=\left(m+n\right)\left(mn+d^2\right)=a\left(mn+d^2\right)=mb^2+nc^2 }[/math].