피타고라스 정리

개요

고대 그리스의 수학자인 피타고라스의 이름을 따서 지은 정리인 피타고라스 정리(Pythagorean theorem, Pythagoras' theorem)는 유클리드 공간에서 직각삼각형에서 성립하는 식을 담고 있다. 빗변의 길이를 [math]\displaystyle{ c }[/math]라고 하고, 다른 두 변의 길이를 [math]\displaystyle{ a,b }[/math]라고 했을 때,

[math]\displaystyle{ \displaystyle{a^2 + b^2 = c^2} }[/math]

이 성립한다.

이 정리는 피타고라스가 활동하던 고대 그리스 시대 이전부터 잘 알려져 있었다. 한 기록에는 피타고라스가 발견하기 한참 전에 고대 중국에서 이 정리를 알고 있었다는 내용도 있다. 다만, 피타고라스의 이름을 따 지은 것은 피타고라스가 정리를 처음으로 증명했기 때문이다.

이 정리는 물론 여러 의미가 있지만, 넓이는 길이의 제곱에 비례한다는 의미와 유클리드 공간에서는 직각삼각형으로 거리가 주어진다는 의미가 주된 의미이다.

증명

매우 간단한 식인 만큼, 증명도 수백가지가 넘는다. 여기에 그 많은 방법을 다 적을 순 없으니 대표적인 몇 가지만 기술한다.

피타고라스

피타고라스의 방법은 두 가지가 있다.

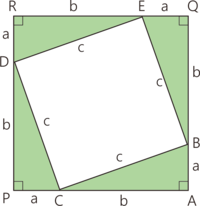
그림에서 [math]\displaystyle{ \triangle ABC \equiv \triangle BEQ \equiv \triangle DER \equiv \triangle CDP }[/math]이고 [math]\displaystyle{ \Box BCDE }[/math]는 정사각형이다. 따라서 [math]\displaystyle{ \Box APRQ = 4 \triangle ABC + \Box BCDE }[/math]이고 이를 [math]\displaystyle{ a, b, c }[/math]로 나타내면 [math]\displaystyle{ (a+b)^2=c^2+4\times{ab \over 2} }[/math]. 괄호를 풀고 분수를 정리하면 [math]\displaystyle{ a^2+2ab+b^2=c^2+2ab }[/math], 양변에서 [math]\displaystyle{ 2ab }[/math]를 빼면 [math]\displaystyle{ a^2+b^2=c^2 }[/math], 피타고라스의 정리가 된다.

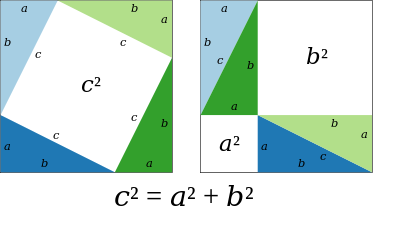
직각삼각형의 배열을 이용하는 방법도 있다. 양 그림에서 흰색 부분에 해당하는 넓이는 같다. 이 흰색 부분에 해당하는 넓이는 다른 직각삼각형 네 개를 어떻게 배열하냐에 따라 다르게 표현할 수 있는데, 왼쪽에서는 [math]\displaystyle{ c^2 }[/math], 오른쪽에서는 [math]\displaystyle{ a^2+b^2 }[/math]이다. 따라서 [math]\displaystyle{ a^2+b^2=c^2 }[/math]

유클리드

각 변의 제곱은 그 변의 길이를 한 변으로 하는 정사각형으로 나타낼 수 있다. 위 그림에서, [math]\displaystyle{ S_{\triangle{AFB}}=S_{\triangle{FCB}}=S_{\triangle{ABD}}=S_{\triangle{BKD}} }[/math]이고, 같은 방법으로 [math]\displaystyle{ S_{\triangle{ACI}}=S_{\triangle{CKE}} }[/math]를 보일 수 있다 (평행한 두 선 사이의 밑변의 길이가 같은 삼각형은 넓이가 모두 같다는 평행사변형의 성질을 이용한다). 이걸 식으로 나타내면 [math]\displaystyle{ \frac{1}{2}a^2+\frac{1}{2}b^2=\frac{1}{2}c^2 }[/math]이고, 따라서 [math]\displaystyle{ a^2+b^2=c^2 }[/math]이다.

참고로 이 방법은 대부분의 교과서에도 나와있는 대표적인 방법.

바스카라

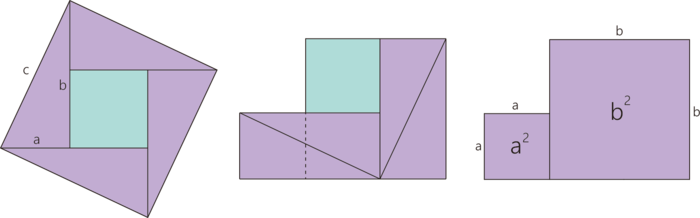
직관적으로 알 수 있는 가장 쉬운 방법이다. 첫 번째 그림은 밑변이 [math]\displaystyle{ a }[/math], 높이가 [math]\displaystyle{ b }[/math]인 직각삼각형 4개와 한 변의 길이가 [math]\displaystyle{ b-a }[/math]인 정사각형으로 구성된 한 변이 [math]\displaystyle{ c }[/math]이고 넓이가 [math]\displaystyle{ c^2 }[/math]인 정사각형이다. 그리고 직각삼각형을 재배치하면 두 번째 그림처럼 되는데 이는 세 번째 그림에서 알 수 있듯이 넓이가 [math]\displaystyle{ a^2 }[/math]인 정사각형과 넓이가 [math]\displaystyle{ b^2 }[/math]인 정사각형 두 개인 것을 알 수 있다. 앞서 재배치하기 전의 정사각형이 [math]\displaystyle{ c^2 }[/math]이고 이를 재배치한 것이 [math]\displaystyle{ a^2+b^2 }[/math]이니 [math]\displaystyle{ c^2=a^2+b^2 }[/math]이다.

가필드

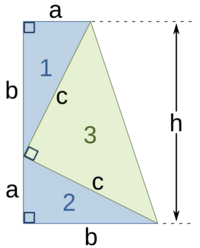
위 사다리꼴의 넓이는 [math]\displaystyle{ \frac{1}{2}\left(a+b\right)\left(a+b\right)=\frac{a^2+b^2+2ab}{2} }[/math]이다. 한편, 넓이를 세 직각삼각형의 넓이의 합으로도 나타낼 수 있는데, 이 경우 [math]\displaystyle{ 2\cdot\frac{1}{2}ab+\frac{1}{2}c^2=ab+\frac{c^2}{2} }[/math]이다. 곧, [math]\displaystyle{ \frac{a^2+b^2+2ab}{2}=ab+\frac{c^2}{2} }[/math]이고, 정리하면 [math]\displaystyle{ a^2+b^2=c^2 }[/math]이다.

피타고라스 수

자연수 중에서 피타고라스 정리를 만족하는 세 수를 피타고라스 수라고 한다. 즉, 직각삼각형을 만드는 자연수 길이의 세 쌍이다. 가장 작은 피타고라스 수는 [math]\displaystyle{ (3,4,5) }[/math]이다. 세 수는 다음과 같이 3개의 자연수로 유일하게 나타낼 수 있다.

[math]\displaystyle{ a = k \cdot (m^2 - n^2) , b = k \cdot (2mn) , c = k \cdot (m^2 + n^2) }[/math]

단, [math]\displaystyle{ n \lt m }[/math]이고, [math]\displaystyle{ m-n }[/math]가 홀수이며, [math]\displaystyle{ m,n }[/math]은 서로소이다.

다음은 몇 가지 피타고라스 수를 나열한 것이다.

[math]\displaystyle{ (3, 4, 5), (11, 60, 61), (16, 63, 65) }[/math]

[math]\displaystyle{ (33, 56, 65), (5, 12, 13), (13, 84, 85) }[/math]

[math]\displaystyle{ (20, 21, 29), (39, 80, 89), (7, 24, 25) }[/math]

[math]\displaystyle{ (8, 15, 17), (28, 45, 53), (48, 55, 73) }[/math]

[math]\displaystyle{ (9, 40, 41), (12, 35, 37), (36, 77, 85), (65, 72, 97) }[/math]

이외에도 [math]\displaystyle{ (6, 8, 10), (9, 12, 15) }[/math]와 같이 피타고라스 수에 자연수를 곱해도 피타고라스 수이고, 원래 삼각형과 닮음이다. 당연하게도 기존 피타고라스 수의 자연수 곱을 제외하더라도 이 피타고라스의 수 역시 무한대로 많다.

여담

피타고라스 학파는 유리수만이 수의 전부라고 믿었다. 그런데, 피타고리스 학파의 한 학자인 히파수스가 짧은 두 변이 1이면 빗변의 길이가 [math]\displaystyle{ \sqrt{2} }[/math]인데, 이 수는 유리수가 아니다는 사실을 알아챘고, 피타고라스 학파는 혼란에 빠졋다. 이후 이 말을 들은 피타고라스는 자신이 믿고 있는 이치에 맞지 않다고 여겨 히파수스를 죽였다느니, 히파수스가 세상에 무리수의 존재를 알리려다가 암살당했다느니 하는 이야기가 있는 반면, 히파수스가 피타고라스 학파의 신념을 지키기 위해 자살했다는 얘기도 있다. 에라 모르겠다! 유리수 빼곤 다 수가 아니야! 하지만 어느쪽이든 진실은 불명이며, 심지어는 히파수스가 무리수를 발견했다는 사실이 맞는지도 의문에 싸여있다.

중학교 수학에서는 그 중요성으로 인해 아예 단원 하나를 차지하고 있다.