편집 요약 없음 |
편집 요약 없음 |
||
| 2번째 줄: | 2번째 줄: | ||
== 역사 == | == 역사 == | ||
[[극한]]이라는 개념은 [[제논의 역설]]에서 알 수 있듯이 고대부터 존재해왔다. 당시에 사용된 극한의 예는 [[원 (도형)|원]]에 내접, 외접하는 [[다각형]]의 넓이를 사용해 원의 넓이를 추정한 것 등이 있다. 그 후, 세월이 흘러 뉴턴이 [[미적분학]]을 연구, 발표하면서 ''직관''에 의존하는 극한의 개념을 이끌어 낸다. 당시로서는 극한값을 구하는 것에만 치중하였고, 수학적으로 엄밀한 연구는 하지 않았다. 현대에 쓰이는 <math>\displaystyle \varepsilon\text{-}N</math> 논법은 볼차노와 바이어슈트라스에 의해 완성된 것이다.<ref><math>\varepsilon\text{-}\delta</math> 논법은 코시에 의해 완성되었다.</ref> | [[극한]]이라는 개념은 [[제논의 역설]]에서 알 수 있듯이 고대부터 존재해왔다. 당시에 사용된 극한의 예는 [[원 (도형)|원]]에 내접, 외접하는 [[다각형]]의 넓이를 사용해 원의 넓이를 추정한 것 등이 있다. 그 후, 세월이 흘러 뉴턴이 [[미적분학]]을 연구, 발표하면서 ''직관''에 의존하는 극한의 개념을 이끌어 낸다. 당시로서는 극한값을 구하는 것에만 치중하였고, 수학적으로 엄밀한 연구는 하지 않았다. 현대에 쓰이는 <math>\displaystyle \displaystyle \varepsilon\text{-}N</math> 논법은 볼차노와 바이어슈트라스에 의해 완성된 것이다.<ref><math>\displaystyle \varepsilon\text{-}\delta</math> 논법은 코시에 의해 완성되었다.</ref> | ||
== 정의 == | == 정의 == | ||
=== 엄밀하지 않은 정의 === | === 엄밀하지 않은 정의 === | ||
실수열 <math>\displaystyle (a_n)</math>이 주어졌다고 하자. ''n''이 커질수록 <math>\displaystyle a_n</math>이 특정한 값 ''L''에 한없이 가까이 다가갈 때, <math>(a_n)</math>은 '''''L''에 수렴한다(converges to ''L'')'''고 하고, | 실수열 <math>\displaystyle \displaystyle (a_n)</math>이 주어졌다고 하자. ''n''이 커질수록 <math>\displaystyle \displaystyle a_n</math>이 특정한 값 ''L''에 한없이 가까이 다가갈 때, <math>\displaystyle (a_n)</math>은 '''''L''에 수렴한다(converges to ''L'')'''고 하고, | ||
: <math>\displaystyle \lim_{n\to\infty}a_n=L</math> | : <math>\displaystyle \displaystyle \lim_{n\to\infty}a_n=L</math> | ||
로 표기한다. 만약 <math>(a_n)</math>이 수렴하지 않으면 '''발산한다(diverges)'''고 한다. | 로 표기한다. 만약 <math>\displaystyle (a_n)</math>이 수렴하지 않으면 '''발산한다(diverges)'''고 한다. | ||
=== 실해석학에서 === | === 실해석학에서 === | ||
실수열 <math>(a_n)</math>이 주어졌다고 하자. 임의의 실수 <math>\varepsilon > 0</math>에 대해 적당한 <math>N\in\mathbb{N}</math>이 존재하여 모든 <math>n > N \left(n\in\mathbb{N}\right)</math><ref>등호가 성립해도 상관 없다.</ref>에 대해 <math>|a_n - L|< \varepsilon</math>일 때, <math>(a_n)</math>은 ''L''에 수렴한다고 한다. | 실수열 <math>\displaystyle (a_n)</math>이 주어졌다고 하자. 임의의 실수 <math>\displaystyle \varepsilon > 0</math>에 대해 적당한 <math>\displaystyle N\in\mathbb{N}</math>이 존재하여 모든 <math>\displaystyle n > N \left(n\in\mathbb{N}\right)</math><ref>등호가 성립해도 상관 없다.</ref>에 대해 <math>\displaystyle |a_n - L|< \varepsilon</math>일 때, <math>\displaystyle (a_n)</math>은 ''L''에 수렴한다고 한다. | ||
== 예시 == | == 예시 == | ||
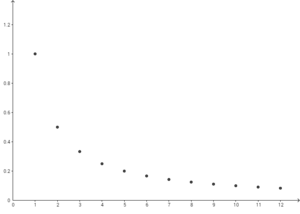
[[파일:1overnfrom1to12.png|섬네일|<math>\frac{1}{n}</math>은 ''n''이 커질수록 0으로 한없이 가까이 다가간다.]] | [[파일:1overnfrom1to12.png|섬네일|<math>\displaystyle \frac{1}{n}</math>은 ''n''이 커질수록 0으로 한없이 가까이 다가간다.]] | ||
<math>a_n=\frac{1}{n}</math>인 수열 <math>\left\{a_n\right\}</math>를 생각하자. 직관적으로 생각하였을 때, <math>n</math>이 커지면 일반항은 0으로 다가간다는 사실을 알 수 있다. 이제 이를 수열의 극한의 엄밀한 정의를 사용해 증명해보자. | <math>\displaystyle a_n=\frac{1}{n}</math>인 수열 <math>\displaystyle \left\{a_n\right\}</math>를 생각하자. 직관적으로 생각하였을 때, <math>\displaystyle n</math>이 커지면 일반항은 0으로 다가간다는 사실을 알 수 있다. 이제 이를 수열의 극한의 엄밀한 정의를 사용해 증명해보자. | ||
임의의 <math>\varepsilon>0</math>에 대해, <math>\frac{1}{N}<\varepsilon</math>를 만족시키는 자연수 <math>N</math>을 찾을 수 있다.<ref>[[아르키메데스 성질]]에 의해 성립한다.</ref> 그럼 <math>n\geq N</math>일 때, <math>\left|a_n-0\right|=\left|\frac{1}{n}\right|\leq\left|\frac{1}{N}\right|=\frac{1}{N}<\varepsilon</math>이므로, 수열의 극한의 정의에 의해 <math>\displaystyle \lim_{n\to\infty}a_n=0</math>이다. | 임의의 <math>\displaystyle \varepsilon>0</math>에 대해, <math>\displaystyle \frac{1}{N}<\varepsilon</math>를 만족시키는 자연수 <math>\displaystyle N</math>을 찾을 수 있다.<ref>[[아르키메데스 성질]]에 의해 성립한다.</ref> 그럼 <math>\displaystyle n\geq N</math>일 때, <math>\displaystyle \left|a_n-0\right|=\left|\frac{1}{n}\right|\leq\left|\frac{1}{N}\right|=\frac{1}{N}<\varepsilon</math>이므로, 수열의 극한의 정의에 의해 <math>\displaystyle \displaystyle \lim_{n\to\infty}a_n=0</math>이다. | ||
== 성질 == | == 성질 == | ||
=== 연산 === | === 연산 === | ||
'''수렴하는''' [[수열]] <math>(a_n),(b_n)</math>에 대해 다음 식이 성립한다. | '''수렴하는''' [[수열]] <math>\displaystyle (a_n),(b_n)</math>에 대해 다음 식이 성립한다. | ||
* <math>\displaystyle \lim_{n\to\infty} ca_n = c\lim_{n\to\infty}a_n</math> | * <math>\displaystyle \displaystyle \lim_{n\to\infty} ca_n = c\lim_{n\to\infty}a_n</math> | ||
<math>\displaystyle \lim_{n\to\infty}a_n=L</math>이라고 하자. 그러면 임의의 <math>\varepsilon >0</math>에 대해 <math>N\in \mathbb{N}</math>이 존재하여 임의의 <math>n\in \mathbb{N}</math>에 대해 <math>n> N</math>이면 <math>|a_n-L|< \frac{\varepsilon}{|c|+1}</math>이다. 그러면 | <math>\displaystyle \displaystyle \lim_{n\to\infty}a_n=L</math>이라고 하자. 그러면 임의의 <math>\displaystyle \varepsilon >0</math>에 대해 <math>\displaystyle N\in \mathbb{N}</math>이 존재하여 임의의 <math>\displaystyle n\in \mathbb{N}</math>에 대해 <math>\displaystyle n> N</math>이면 <math>\displaystyle |a_n-L|< \frac{\varepsilon}{|c|+1}</math>이다. 그러면 | ||
: <math>|c||a_n-L|=|ca_n-cL|<\frac{|c|}{|c|+1}\varepsilon < \varepsilon</math> | : <math>\displaystyle |c||a_n-L|=|ca_n-cL|<\frac{|c|}{|c|+1}\varepsilon < \varepsilon</math> | ||
이므로 원하는 결론을 얻는다. | 이므로 원하는 결론을 얻는다. | ||
* <math>\displaystyle \lim_{n\to\infty} (a_n +b_n)=\lim_{n\to\infty}a_n+\lim_{n\to\infty}b_n</math> | * <math>\displaystyle \displaystyle \lim_{n\to\infty} (a_n +b_n)=\lim_{n\to\infty}a_n+\lim_{n\to\infty}b_n</math> | ||
<math>\displaystyle \lim_{n\to\infty}b_n=M</math>이라고 하자. 그러면 임의의 <math>\varepsilon >0</math>에 대해 <math>N_1,N_2\in \mathbb{N}</math>가 존재하여 임의의 <math>n\in \mathbb{N}</math>에 대해 각각 <math>n> N_1,n> N_2</math>이면 <math>|a_n-L|< \frac{\varepsilon}{2},|b_n-M|< \frac{\varepsilon}{2}</math>이다. 그러면 임의의 <math>\varepsilon>0</math>에 대해 <math>\max\{N_1,N_2\}</math>가 존재하여 임의의 <math>n > \max\{N_1,N_2\}</math>에 대해 [[삼각부등식]]에 의해 | <math>\displaystyle \displaystyle \lim_{n\to\infty}b_n=M</math>이라고 하자. 그러면 임의의 <math>\displaystyle \varepsilon >0</math>에 대해 <math>\displaystyle N_1,N_2\in \mathbb{N}</math>가 존재하여 임의의 <math>\displaystyle n\in \mathbb{N}</math>에 대해 각각 <math>\displaystyle n> N_1,n> N_2</math>이면 <math>\displaystyle |a_n-L|< \frac{\varepsilon}{2},|b_n-M|< \frac{\varepsilon}{2}</math>이다. 그러면 임의의 <math>\displaystyle \varepsilon>0</math>에 대해 <math>\displaystyle \max\{N_1,N_2\}</math>가 존재하여 임의의 <math>\displaystyle n > \max\{N_1,N_2\}</math>에 대해 [[삼각부등식]]에 의해 | ||
: <math>|(a_n+b_n)-(L+M)|=|(a_n-L)+(b_n-M)|\le|a_n-L|+|b_n-M| < \frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon</math> | : <math>\displaystyle |(a_n+b_n)-(L+M)|=|(a_n-L)+(b_n-M)|\le|a_n-L|+|b_n-M| < \frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon</math> | ||
이므로 원하는 결론을 얻는다. | 이므로 원하는 결론을 얻는다. | ||
* <math>\displaystyle \lim_{n\to\infty} a_nb_n=\left(\lim_{n\to\infty}a_n\right)\left(\lim_{n\to\infty}b_n\right)</math> | * <math>\displaystyle \displaystyle \lim_{n\to\infty} a_nb_n=\left(\lim_{n\to\infty}a_n\right)\left(\lim_{n\to\infty}b_n\right)</math> | ||
수렴하는 수열은 항상 [[유계]]이다. 즉, 적당한 양의 실수 <math>M</math>에 대해 <math>\left|b_n\right|\leq M,\,\forall n\in\mathbb{N}</math>이다. 두 수열 <math>\left\{a_n\right\},\left\{b_n\right\}</math>의 수렴값을 각각 <math>a,b</math>라고 하자. 그럼, 임의의 <math>\varepsilon>0</math>에 대해 적당한 자연수 <math>N_1</math>이 존재하여 <math>n\geq N_1</math>이면 <math>\left|a_n-a\right|<\frac{\varepsilon}{2M}</math>이 성립한다. 마찬가지로, 적당한 자연수 <math>N_2</math>가 존재하여 <math>n\geq N_2</math>이면 <math>\left|b_n-b\right|<\frac{\varepsilon}{2\left|a\right|+1}</math>이 성립한다. <math>N=\max\left(N_1,N_2\right)</math>라 하자. 그러면, <math>n\geq N</math>에 대해, | 수렴하는 수열은 항상 [[유계]]이다. 즉, 적당한 양의 실수 <math>\displaystyle M</math>에 대해 <math>\displaystyle \left|b_n\right|\leq M,\,\forall n\in\mathbb{N}</math>이다. 두 수열 <math>\displaystyle \left\{a_n\right\},\left\{b_n\right\}</math>의 수렴값을 각각 <math>\displaystyle a,b</math>라고 하자. 그럼, 임의의 <math>\displaystyle \varepsilon>0</math>에 대해 적당한 자연수 <math>\displaystyle N_1</math>이 존재하여 <math>\displaystyle n\geq N_1</math>이면 <math>\displaystyle \left|a_n-a\right|<\frac{\varepsilon}{2M}</math>이 성립한다. 마찬가지로, 적당한 자연수 <math>\displaystyle N_2</math>가 존재하여 <math>\displaystyle n\geq N_2</math>이면 <math>\displaystyle \left|b_n-b\right|<\frac{\varepsilon}{2\left|a\right|+1}</math>이 성립한다. <math>\displaystyle N=\max\left(N_1,N_2\right)</math>라 하자. 그러면, <math>\displaystyle n\geq N</math>에 대해, | ||
:<math>\left|a_nb_n-ab\right|=\left|a_nb_n-ab_n+ab_n-ab\right|\leq\left|b_n\right|\left|a_n-a\right|+\left|a\right|\left|b_n-b\right|< M\cdot\frac{\varepsilon}{2M}+\left|a\right|\cdot\frac{\varepsilon}{2\left|a\right|+1}<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon</math> | :<math>\displaystyle \left|a_nb_n-ab\right|=\left|a_nb_n-ab_n+ab_n-ab\right|\leq\left|b_n\right|\left|a_n-a\right|+\left|a\right|\left|b_n-b\right|< M\cdot\frac{\varepsilon}{2M}+\left|a\right|\cdot\frac{\varepsilon}{2\left|a\right|+1}<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon</math> | ||
이므로 원하는 결론을 얻는다. | 이므로 원하는 결론을 얻는다. | ||
* <math>\displaystyle \lim_{n\to\infty} \frac{a_n}{b_n}=\frac{\lim_{n\to\infty} a_n}{\lim_{n\to\infty} b_n}\text{ if }\lim_{n\to\infty}b_n\ne 0</math> | * <math>\displaystyle \displaystyle \lim_{n\to\infty} \frac{a_n}{b_n}=\frac{\lim_{n\to\infty} a_n}{\lim_{n\to\infty} b_n}\text{ if }\lim_{n\to\infty}b_n\ne 0</math> | ||
<math>\displaystyle \lim_{n\to\infty}\frac{1}{a_n}=\frac{1}{\lim_{n\to\infty}a_n}\text{ if }\lim_{n\to\infty}a_n\neq0</math>만 증명하면 된다. 수렴값을 <math>a</math>라 하자. 그럼, 임의의 <math>\varepsilon>0</math>에 대해 적당한 자연수 <math>N_1</math>가 존재하여, <math>n\geq N_1</math>이면, <math>\left|a_n-a\right|<\frac{\left|a\right|}{2}</math>가 성립한다. [[삼각부등식]] 에 의해, <math>\left|\left|a_n\right|-\left|a\right|\right|<\frac{\left|a\right|}{2}</math>가 성립하고, 좌변의 [[절댓값]]을 벗겨주면, <math>-\frac{\left|a\right|}{2}<\left|a_n\right|-\left|a\right|<\frac{\left|a\right|}{2}</math>가 성립한다. 여기서 <math>\frac{\left|a\right|}{2}<\left|a_n\right|</math>임을 알 수 있다.<ref>이는 곧 극한값이 0이 아니면 어느 한 시점부터는 수열의 값이 전부 0이 아니어야 한다는 것을 의미한다.</ref> 이제, 적당한 자연수 <math>N_2</math>에 대해 <math>n\geq N_2</math>이면 <math>\left|a_n-a\right|<\frac{\left|a\right|^2\varepsilon}{2}</math>가 성립한다. <math>N=\max\left(N_1,N_2\right)</math>이라 해주면, <math>n\geq N</math>일 때, | <math>\displaystyle \displaystyle \lim_{n\to\infty}\frac{1}{a_n}=\frac{1}{\lim_{n\to\infty}a_n}\text{ if }\lim_{n\to\infty}a_n\neq0</math>만 증명하면 된다. 수렴값을 <math>\displaystyle a</math>라 하자. 그럼, 임의의 <math>\displaystyle \varepsilon>0</math>에 대해 적당한 자연수 <math>\displaystyle N_1</math>가 존재하여, <math>\displaystyle n\geq N_1</math>이면, <math>\displaystyle \left|a_n-a\right|<\frac{\left|a\right|}{2}</math>가 성립한다. [[삼각부등식]] 에 의해, <math>\displaystyle \left|\left|a_n\right|-\left|a\right|\right|<\frac{\left|a\right|}{2}</math>가 성립하고, 좌변의 [[절댓값]]을 벗겨주면, <math>\displaystyle -\frac{\left|a\right|}{2}<\left|a_n\right|-\left|a\right|<\frac{\left|a\right|}{2}</math>가 성립한다. 여기서 <math>\displaystyle \frac{\left|a\right|}{2}<\left|a_n\right|</math>임을 알 수 있다.<ref>이는 곧 극한값이 0이 아니면 어느 한 시점부터는 수열의 값이 전부 0이 아니어야 한다는 것을 의미한다.</ref> 이제, 적당한 자연수 <math>\displaystyle N_2</math>에 대해 <math>\displaystyle n\geq N_2</math>이면 <math>\displaystyle \left|a_n-a\right|<\frac{\left|a\right|^2\varepsilon}{2}</math>가 성립한다. <math>\displaystyle N=\max\left(N_1,N_2\right)</math>이라 해주면, <math>\displaystyle n\geq N</math>일 때, | ||
:<math>\left|\frac{1}{a_n}-\frac{1}{a}\right|=\frac{\left|a_n-a\right|}{\left|a_n\right|\left|a\right|}<\frac{2}{\left|a\right|}\cdot\frac{1}{\left|a\right|}\cdot\frac{\left|a\right|^2\varepsilon}{2}=\varepsilon</math> | :<math>\displaystyle \left|\frac{1}{a_n}-\frac{1}{a}\right|=\frac{\left|a_n-a\right|}{\left|a_n\right|\left|a\right|}<\frac{2}{\left|a\right|}\cdot\frac{1}{\left|a\right|}\cdot\frac{\left|a\right|^2\varepsilon}{2}=\varepsilon</math> | ||
이 되어 원하는 결론을 얻는다. | 이 되어 원하는 결론을 얻는다. | ||
=== 유일성 === | === 유일성 === | ||
앞에서 <math>a_n=\frac{1}{n}</math>인 수열 <math>(a_n)</math>의 극한값이 0임을 보였지만, 다른 극한값이 또 있는 건 아닌지 의심해볼 수 있다. 다행스럽게도 0 말고 다른 극한값은 존재하지 않는다. 일반적으로 실수열의 극한값이 유일함을 보일 수 있다. | 앞에서 <math>\displaystyle a_n=\frac{1}{n}</math>인 수열 <math>\displaystyle (a_n)</math>의 극한값이 0임을 보였지만, 다른 극한값이 또 있는 건 아닌지 의심해볼 수 있다. 다행스럽게도 0 말고 다른 극한값은 존재하지 않는다. 일반적으로 실수열의 극한값이 유일함을 보일 수 있다. | ||
<math>L_1,L_2</math>를 수열 <math>(a_n)</math>의 극한값이라고 하자. 그러면 극한의 정의에 의해 임의의 <math>\varepsilon >0</math>에 대해 <math>N\in\mathbb{N}</math>이 존재하여 임의의 <math>n\in \mathbb{N}</math>에 대해 <math>n > N</math>이면 <math>|a_n - L_1 | < \frac{\varepsilon}{2}</math>이고 <math>|a_n - L_2|<\frac{\varepsilon}{2}</math>이다. 그러면 [[삼각부등식]]에 의해 | <math>\displaystyle L_1,L_2</math>를 수열 <math>\displaystyle (a_n)</math>의 극한값이라고 하자. 그러면 극한의 정의에 의해 임의의 <math>\displaystyle \varepsilon >0</math>에 대해 <math>\displaystyle N\in\mathbb{N}</math>이 존재하여 임의의 <math>\displaystyle n\in \mathbb{N}</math>에 대해 <math>\displaystyle n > N</math>이면 <math>\displaystyle |a_n - L_1 | < \frac{\varepsilon}{2}</math>이고 <math>\displaystyle |a_n - L_2|<\frac{\varepsilon}{2}</math>이다. 그러면 [[삼각부등식]]에 의해 | ||
: <math>|L_1 - L_2 | = |(a_n - L_2)-(a_n-L_1)|\le | a_n - L_2|+|a_n-L_1| < \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon</math> | : <math>\displaystyle |L_1 - L_2 | = |(a_n - L_2)-(a_n-L_1)|\le | a_n - L_2|+|a_n-L_1| < \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon</math> | ||
이다. 이 부등식이 임의의 <math>\varepsilon > 0 </math>에 대해 성립하므로 <math>L_1=L_2</math>임을 알 수 있다. | 이다. 이 부등식이 임의의 <math>\displaystyle \varepsilon > 0 </math>에 대해 성립하므로 <math>\displaystyle L_1=L_2</math>임을 알 수 있다. | ||
== 확장 == | == 확장 == | ||
=== 복소해석학에서 === | === 복소해석학에서 === | ||
복소수열 <math>(z_n)</math>이 주어졌다고 하자. 임의의 실수 <math>\varepsilon >0 </math>에 대해 적당한 <math>N\in\mathbb{N}</math>이 존재하여 모든 <math>n > N \left(n\in\mathbb{N}\right)</math>에 대해 <math>|z_n - L|< \varepsilon</math>일 때, <math>(z_n)</math>은 ''L''에 수렴한다고 한다. | 복소수열 <math>\displaystyle (z_n)</math>이 주어졌다고 하자. 임의의 실수 <math>\displaystyle \varepsilon >0 </math>에 대해 적당한 <math>\displaystyle N\in\mathbb{N}</math>이 존재하여 모든 <math>\displaystyle n > N \left(n\in\mathbb{N}\right)</math>에 대해 <math>\displaystyle |z_n - L|< \varepsilon</math>일 때, <math>\displaystyle (z_n)</math>은 ''L''에 수렴한다고 한다. | ||
=== 거리공간에서 === | === 거리공간에서 === | ||
<math>(X,d)</math>가 [[거리공간]]이고 <math>(x_n)</math>을 ''X''의 점열이라고 하자. 임의의 실수 <math>\varepsilon > 0</math>에 대해 적당한 <math>N\in \mathbb{N}</math>이 존재하여 모든 <math>n > N \left(n\in\mathbb{N}\right)</math>에 대해 <math>d \left( x_n , x \right) < \varepsilon</math>일 때, <math>(x_n)</math>은 ''x''에 수렴한다고 한다. | <math>\displaystyle (X,d)</math>가 [[거리공간]]이고 <math>\displaystyle (x_n)</math>을 ''X''의 점열이라고 하자. 임의의 실수 <math>\displaystyle \varepsilon > 0</math>에 대해 적당한 <math>\displaystyle N\in \mathbb{N}</math>이 존재하여 모든 <math>\displaystyle n > N \left(n\in\mathbb{N}\right)</math>에 대해 <math>\displaystyle d \left( x_n , x \right) < \varepsilon</math>일 때, <math>\displaystyle (x_n)</math>은 ''x''에 수렴한다고 한다. | ||
=== 위상공간에서 === | === 위상공간에서 === | ||
<math>(X,\mathcal{T})</math>가 [[위상공간]]이고 <math>(x_n)</math>은 ''X''의 점열이라고 하자. ''x''를 포함하는 임의의 [[열린 집합]] ''O''에 대해 적당한 <math>N\in\mathbb{N}</math>이 존재하여 모든 <math>n > N \left(n\in\mathbb{N}\right)</math>에 대해 <math>x_n \in O</math>일 때, <math>(x_n)</math>은 ''x''에 수렴한다고 한다. | <math>\displaystyle (X,\mathcal{T})</math>가 [[위상공간]]이고 <math>\displaystyle (x_n)</math>은 ''X''의 점열이라고 하자. ''x''를 포함하는 임의의 [[열린 집합]] ''O''에 대해 적당한 <math>\displaystyle N\in\mathbb{N}</math>이 존재하여 모든 <math>\displaystyle n > N \left(n\in\mathbb{N}\right)</math>에 대해 <math>\displaystyle x_n \in O</math>일 때, <math>\displaystyle (x_n)</math>은 ''x''에 수렴한다고 한다. | ||
일반적으로 위상공간에선 점열의 극한이 유일하지 않다. | 일반적으로 위상공간에선 점열의 극한이 유일하지 않다. | ||
<math>\mathbb{R}</math> 위의 [[유한여집합위상]]을 <math>\mathcal{T}</math>라고 하자. 이때 위상공간 <math>(\mathbb{R},\mathcal{T})</math>에서 정의된 서로 다른 점들의 점열을 <math>(x_n)</math>이라고 하자. <math>x\in \mathbb{R}</math>를 포함하는 임의의 열린 집합 <math>O</math>에 대해 <math>\mathbb{X}\setminus O</math>는 위상의 정의에 의해 유한집합이다. 즉 <math>x_n \not\in O</math>인 원소는 많아봐야 유한 개이므로 <math>x_N\not\in O</math>인 가장 큰 <math>N\in \mathbb{N}</math>이 존재한다. 즉, 임의의 자연수 <math>n> N</math>에 대해 <math>x_n\in O</math>이므로 <math>(x_n)</math>은 <math>x</math>에 수렴한다. <math>x</math>가 임의의 실수이므로, <math>(x_n)</math>은 임의의 실수에 수렴한다. | <math>\displaystyle \mathbb{R}</math> 위의 [[유한여집합위상]]을 <math>\displaystyle \mathcal{T}</math>라고 하자. 이때 위상공간 <math>\displaystyle (\mathbb{R},\mathcal{T})</math>에서 정의된 서로 다른 점들의 점열을 <math>\displaystyle (x_n)</math>이라고 하자. <math>\displaystyle x\in \mathbb{R}</math>를 포함하는 임의의 열린 집합 <math>\displaystyle O</math>에 대해 <math>\displaystyle \mathbb{X}\setminus O</math>는 위상의 정의에 의해 유한집합이다. 즉 <math>\displaystyle x_n \not\in O</math>인 원소는 많아봐야 유한 개이므로 <math>\displaystyle x_N\not\in O</math>인 가장 큰 <math>\displaystyle N\in \mathbb{N}</math>이 존재한다. 즉, 임의의 자연수 <math>\displaystyle n> N</math>에 대해 <math>\displaystyle x_n\in O</math>이므로 <math>\displaystyle (x_n)</math>은 <math>\displaystyle x</math>에 수렴한다. <math>\displaystyle x</math>가 임의의 실수이므로, <math>\displaystyle (x_n)</math>은 임의의 실수에 수렴한다. | ||
[[하우스도르프 공간]]에서 수렴하는 점열의 극한값은 유일하다. | [[하우스도르프 공간]]에서 수렴하는 점열의 극한값은 유일하다. | ||
2019년 10월 16일 (수) 12:00 판
역사
극한이라는 개념은 제논의 역설에서 알 수 있듯이 고대부터 존재해왔다. 당시에 사용된 극한의 예는 원에 내접, 외접하는 다각형의 넓이를 사용해 원의 넓이를 추정한 것 등이 있다. 그 후, 세월이 흘러 뉴턴이 미적분학을 연구, 발표하면서 직관에 의존하는 극한의 개념을 이끌어 낸다. 당시로서는 극한값을 구하는 것에만 치중하였고, 수학적으로 엄밀한 연구는 하지 않았다. 현대에 쓰이는 [math]\displaystyle{ \displaystyle \displaystyle \varepsilon\text{-}N }[/math] 논법은 볼차노와 바이어슈트라스에 의해 완성된 것이다.[1]
정의
엄밀하지 않은 정의
실수열 [math]\displaystyle{ \displaystyle \displaystyle (a_n) }[/math]이 주어졌다고 하자. n이 커질수록 [math]\displaystyle{ \displaystyle \displaystyle a_n }[/math]이 특정한 값 L에 한없이 가까이 다가갈 때, [math]\displaystyle{ \displaystyle (a_n) }[/math]은 L에 수렴한다(converges to L)고 하고,
- [math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty}a_n=L }[/math]
로 표기한다. 만약 [math]\displaystyle{ \displaystyle (a_n) }[/math]이 수렴하지 않으면 발산한다(diverges)고 한다.
실해석학에서
실수열 [math]\displaystyle{ \displaystyle (a_n) }[/math]이 주어졌다고 하자. 임의의 실수 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 적당한 [math]\displaystyle{ \displaystyle N\in\mathbb{N} }[/math]이 존재하여 모든 [math]\displaystyle{ \displaystyle n \gt N \left(n\in\mathbb{N}\right) }[/math][2]에 대해 [math]\displaystyle{ \displaystyle |a_n - L|\lt \varepsilon }[/math]일 때, [math]\displaystyle{ \displaystyle (a_n) }[/math]은 L에 수렴한다고 한다.
예시
[math]\displaystyle{ \displaystyle a_n=\frac{1}{n} }[/math]인 수열 [math]\displaystyle{ \displaystyle \left\{a_n\right\} }[/math]를 생각하자. 직관적으로 생각하였을 때, [math]\displaystyle{ \displaystyle n }[/math]이 커지면 일반항은 0으로 다가간다는 사실을 알 수 있다. 이제 이를 수열의 극한의 엄밀한 정의를 사용해 증명해보자.
임의의 [math]\displaystyle{ \displaystyle \varepsilon\gt 0 }[/math]에 대해, [math]\displaystyle{ \displaystyle \frac{1}{N}\lt \varepsilon }[/math]를 만족시키는 자연수 [math]\displaystyle{ \displaystyle N }[/math]을 찾을 수 있다.[3] 그럼 [math]\displaystyle{ \displaystyle n\geq N }[/math]일 때, [math]\displaystyle{ \displaystyle \left|a_n-0\right|=\left|\frac{1}{n}\right|\leq\left|\frac{1}{N}\right|=\frac{1}{N}\lt \varepsilon }[/math]이므로, 수열의 극한의 정의에 의해 [math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty}a_n=0 }[/math]이다.
성질
연산
수렴하는 수열 [math]\displaystyle{ \displaystyle (a_n),(b_n) }[/math]에 대해 다음 식이 성립한다.
- [math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty} ca_n = c\lim_{n\to\infty}a_n }[/math]
[math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty}a_n=L }[/math]이라고 하자. 그러면 임의의 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 [math]\displaystyle{ \displaystyle N\in \mathbb{N} }[/math]이 존재하여 임의의 [math]\displaystyle{ \displaystyle n\in \mathbb{N} }[/math]에 대해 [math]\displaystyle{ \displaystyle n\gt N }[/math]이면 [math]\displaystyle{ \displaystyle |a_n-L|\lt \frac{\varepsilon}{|c|+1} }[/math]이다. 그러면
- [math]\displaystyle{ \displaystyle |c||a_n-L|=|ca_n-cL|\lt \frac{|c|}{|c|+1}\varepsilon \lt \varepsilon }[/math]
이므로 원하는 결론을 얻는다.
- [math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty} (a_n +b_n)=\lim_{n\to\infty}a_n+\lim_{n\to\infty}b_n }[/math]
[math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty}b_n=M }[/math]이라고 하자. 그러면 임의의 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 [math]\displaystyle{ \displaystyle N_1,N_2\in \mathbb{N} }[/math]가 존재하여 임의의 [math]\displaystyle{ \displaystyle n\in \mathbb{N} }[/math]에 대해 각각 [math]\displaystyle{ \displaystyle n\gt N_1,n\gt N_2 }[/math]이면 [math]\displaystyle{ \displaystyle |a_n-L|\lt \frac{\varepsilon}{2},|b_n-M|\lt \frac{\varepsilon}{2} }[/math]이다. 그러면 임의의 [math]\displaystyle{ \displaystyle \varepsilon\gt 0 }[/math]에 대해 [math]\displaystyle{ \displaystyle \max\{N_1,N_2\} }[/math]가 존재하여 임의의 [math]\displaystyle{ \displaystyle n \gt \max\{N_1,N_2\} }[/math]에 대해 삼각부등식에 의해
- [math]\displaystyle{ \displaystyle |(a_n+b_n)-(L+M)|=|(a_n-L)+(b_n-M)|\le|a_n-L|+|b_n-M| \lt \frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon }[/math]
이므로 원하는 결론을 얻는다.
- [math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty} a_nb_n=\left(\lim_{n\to\infty}a_n\right)\left(\lim_{n\to\infty}b_n\right) }[/math]
수렴하는 수열은 항상 유계이다. 즉, 적당한 양의 실수 [math]\displaystyle{ \displaystyle M }[/math]에 대해 [math]\displaystyle{ \displaystyle \left|b_n\right|\leq M,\,\forall n\in\mathbb{N} }[/math]이다. 두 수열 [math]\displaystyle{ \displaystyle \left\{a_n\right\},\left\{b_n\right\} }[/math]의 수렴값을 각각 [math]\displaystyle{ \displaystyle a,b }[/math]라고 하자. 그럼, 임의의 [math]\displaystyle{ \displaystyle \varepsilon\gt 0 }[/math]에 대해 적당한 자연수 [math]\displaystyle{ \displaystyle N_1 }[/math]이 존재하여 [math]\displaystyle{ \displaystyle n\geq N_1 }[/math]이면 [math]\displaystyle{ \displaystyle \left|a_n-a\right|\lt \frac{\varepsilon}{2M} }[/math]이 성립한다. 마찬가지로, 적당한 자연수 [math]\displaystyle{ \displaystyle N_2 }[/math]가 존재하여 [math]\displaystyle{ \displaystyle n\geq N_2 }[/math]이면 [math]\displaystyle{ \displaystyle \left|b_n-b\right|\lt \frac{\varepsilon}{2\left|a\right|+1} }[/math]이 성립한다. [math]\displaystyle{ \displaystyle N=\max\left(N_1,N_2\right) }[/math]라 하자. 그러면, [math]\displaystyle{ \displaystyle n\geq N }[/math]에 대해,
- [math]\displaystyle{ \displaystyle \left|a_nb_n-ab\right|=\left|a_nb_n-ab_n+ab_n-ab\right|\leq\left|b_n\right|\left|a_n-a\right|+\left|a\right|\left|b_n-b\right|\lt M\cdot\frac{\varepsilon}{2M}+\left|a\right|\cdot\frac{\varepsilon}{2\left|a\right|+1}\lt \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon }[/math]
이므로 원하는 결론을 얻는다.
- [math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty} \frac{a_n}{b_n}=\frac{\lim_{n\to\infty} a_n}{\lim_{n\to\infty} b_n}\text{ if }\lim_{n\to\infty}b_n\ne 0 }[/math]
[math]\displaystyle{ \displaystyle \displaystyle \lim_{n\to\infty}\frac{1}{a_n}=\frac{1}{\lim_{n\to\infty}a_n}\text{ if }\lim_{n\to\infty}a_n\neq0 }[/math]만 증명하면 된다. 수렴값을 [math]\displaystyle{ \displaystyle a }[/math]라 하자. 그럼, 임의의 [math]\displaystyle{ \displaystyle \varepsilon\gt 0 }[/math]에 대해 적당한 자연수 [math]\displaystyle{ \displaystyle N_1 }[/math]가 존재하여, [math]\displaystyle{ \displaystyle n\geq N_1 }[/math]이면, [math]\displaystyle{ \displaystyle \left|a_n-a\right|\lt \frac{\left|a\right|}{2} }[/math]가 성립한다. 삼각부등식 에 의해, [math]\displaystyle{ \displaystyle \left|\left|a_n\right|-\left|a\right|\right|\lt \frac{\left|a\right|}{2} }[/math]가 성립하고, 좌변의 절댓값을 벗겨주면, [math]\displaystyle{ \displaystyle -\frac{\left|a\right|}{2}\lt \left|a_n\right|-\left|a\right|\lt \frac{\left|a\right|}{2} }[/math]가 성립한다. 여기서 [math]\displaystyle{ \displaystyle \frac{\left|a\right|}{2}\lt \left|a_n\right| }[/math]임을 알 수 있다.[4] 이제, 적당한 자연수 [math]\displaystyle{ \displaystyle N_2 }[/math]에 대해 [math]\displaystyle{ \displaystyle n\geq N_2 }[/math]이면 [math]\displaystyle{ \displaystyle \left|a_n-a\right|\lt \frac{\left|a\right|^2\varepsilon}{2} }[/math]가 성립한다. [math]\displaystyle{ \displaystyle N=\max\left(N_1,N_2\right) }[/math]이라 해주면, [math]\displaystyle{ \displaystyle n\geq N }[/math]일 때,
- [math]\displaystyle{ \displaystyle \left|\frac{1}{a_n}-\frac{1}{a}\right|=\frac{\left|a_n-a\right|}{\left|a_n\right|\left|a\right|}\lt \frac{2}{\left|a\right|}\cdot\frac{1}{\left|a\right|}\cdot\frac{\left|a\right|^2\varepsilon}{2}=\varepsilon }[/math]
이 되어 원하는 결론을 얻는다.
유일성
앞에서 [math]\displaystyle{ \displaystyle a_n=\frac{1}{n} }[/math]인 수열 [math]\displaystyle{ \displaystyle (a_n) }[/math]의 극한값이 0임을 보였지만, 다른 극한값이 또 있는 건 아닌지 의심해볼 수 있다. 다행스럽게도 0 말고 다른 극한값은 존재하지 않는다. 일반적으로 실수열의 극한값이 유일함을 보일 수 있다.
[math]\displaystyle{ \displaystyle L_1,L_2 }[/math]를 수열 [math]\displaystyle{ \displaystyle (a_n) }[/math]의 극한값이라고 하자. 그러면 극한의 정의에 의해 임의의 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 [math]\displaystyle{ \displaystyle N\in\mathbb{N} }[/math]이 존재하여 임의의 [math]\displaystyle{ \displaystyle n\in \mathbb{N} }[/math]에 대해 [math]\displaystyle{ \displaystyle n \gt N }[/math]이면 [math]\displaystyle{ \displaystyle |a_n - L_1 | \lt \frac{\varepsilon}{2} }[/math]이고 [math]\displaystyle{ \displaystyle |a_n - L_2|\lt \frac{\varepsilon}{2} }[/math]이다. 그러면 삼각부등식에 의해
- [math]\displaystyle{ \displaystyle |L_1 - L_2 | = |(a_n - L_2)-(a_n-L_1)|\le | a_n - L_2|+|a_n-L_1| \lt \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon }[/math]
이다. 이 부등식이 임의의 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 성립하므로 [math]\displaystyle{ \displaystyle L_1=L_2 }[/math]임을 알 수 있다.
확장
복소해석학에서
복소수열 [math]\displaystyle{ \displaystyle (z_n) }[/math]이 주어졌다고 하자. 임의의 실수 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 적당한 [math]\displaystyle{ \displaystyle N\in\mathbb{N} }[/math]이 존재하여 모든 [math]\displaystyle{ \displaystyle n \gt N \left(n\in\mathbb{N}\right) }[/math]에 대해 [math]\displaystyle{ \displaystyle |z_n - L|\lt \varepsilon }[/math]일 때, [math]\displaystyle{ \displaystyle (z_n) }[/math]은 L에 수렴한다고 한다.
거리공간에서
[math]\displaystyle{ \displaystyle (X,d) }[/math]가 거리공간이고 [math]\displaystyle{ \displaystyle (x_n) }[/math]을 X의 점열이라고 하자. 임의의 실수 [math]\displaystyle{ \displaystyle \varepsilon \gt 0 }[/math]에 대해 적당한 [math]\displaystyle{ \displaystyle N\in \mathbb{N} }[/math]이 존재하여 모든 [math]\displaystyle{ \displaystyle n \gt N \left(n\in\mathbb{N}\right) }[/math]에 대해 [math]\displaystyle{ \displaystyle d \left( x_n , x \right) \lt \varepsilon }[/math]일 때, [math]\displaystyle{ \displaystyle (x_n) }[/math]은 x에 수렴한다고 한다.
위상공간에서
[math]\displaystyle{ \displaystyle (X,\mathcal{T}) }[/math]가 위상공간이고 [math]\displaystyle{ \displaystyle (x_n) }[/math]은 X의 점열이라고 하자. x를 포함하는 임의의 열린 집합 O에 대해 적당한 [math]\displaystyle{ \displaystyle N\in\mathbb{N} }[/math]이 존재하여 모든 [math]\displaystyle{ \displaystyle n \gt N \left(n\in\mathbb{N}\right) }[/math]에 대해 [math]\displaystyle{ \displaystyle x_n \in O }[/math]일 때, [math]\displaystyle{ \displaystyle (x_n) }[/math]은 x에 수렴한다고 한다.
일반적으로 위상공간에선 점열의 극한이 유일하지 않다.
[math]\displaystyle{ \displaystyle \mathbb{R} }[/math] 위의 유한여집합위상을 [math]\displaystyle{ \displaystyle \mathcal{T} }[/math]라고 하자. 이때 위상공간 [math]\displaystyle{ \displaystyle (\mathbb{R},\mathcal{T}) }[/math]에서 정의된 서로 다른 점들의 점열을 [math]\displaystyle{ \displaystyle (x_n) }[/math]이라고 하자. [math]\displaystyle{ \displaystyle x\in \mathbb{R} }[/math]를 포함하는 임의의 열린 집합 [math]\displaystyle{ \displaystyle O }[/math]에 대해 [math]\displaystyle{ \displaystyle \mathbb{X}\setminus O }[/math]는 위상의 정의에 의해 유한집합이다. 즉 [math]\displaystyle{ \displaystyle x_n \not\in O }[/math]인 원소는 많아봐야 유한 개이므로 [math]\displaystyle{ \displaystyle x_N\not\in O }[/math]인 가장 큰 [math]\displaystyle{ \displaystyle N\in \mathbb{N} }[/math]이 존재한다. 즉, 임의의 자연수 [math]\displaystyle{ \displaystyle n\gt N }[/math]에 대해 [math]\displaystyle{ \displaystyle x_n\in O }[/math]이므로 [math]\displaystyle{ \displaystyle (x_n) }[/math]은 [math]\displaystyle{ \displaystyle x }[/math]에 수렴한다. [math]\displaystyle{ \displaystyle x }[/math]가 임의의 실수이므로, [math]\displaystyle{ \displaystyle (x_n) }[/math]은 임의의 실수에 수렴한다.
하우스도르프 공간에서 수렴하는 점열의 극한값은 유일하다.