파스칼의 정리

원에 접하는 (오목) 육각형 ABCDEF에 대해서 파스칼 직선 PQR을 정의할 수 있다.

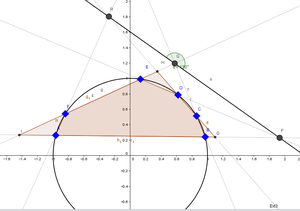
사영기하학에서 파스칼의 정리(다른 말로는 신비한 육각형의 정리)는 원뿔곡선 위에 여섯 개의 점을 잡았을 때 이 여섯 점으로 만든 육각형을 작도했을 때 맞은 편 변에 있는 세 쌍의 변이 각각 만나서 생기는 세 점이 일직선상에 있다는 것을 의미한다. 유클리드 공간에서도 이 정리는 유용하지만 평행선에 대해서도 설명하기 위해서는 사영기하학의 전제가 필요하다.

유클리드 공간에서

이 정리 자체는 사영기하학에서 정의하는 것이 바람직하다. 왜냐하면 사영평면(Projective Plane)상에서는 모든 직선은 만나고, 평행선이 존재하지 않기 때문이다. 하지만 유클리드 공간에서 평행선이 없다는 제한조건을 덧붙이면 유클리드 공간에서도 해당 정리가 유효하다는 것을 알 수 있다.

만일 맞은 변 중에서 단 한 쌍이 평행하고, 나머지 두 쌍은 서로 만난다면, 만나는 두 쌍의 변이 만들어내는 두 교점과 평행한 한 쌍의 변은 서로 평행하게 된다. 만일 맞은 변 중에서 두 쌍이 평행하면 나머지 한 쌍의 변도 무조건 평행하게 된다.

Hexagrammum Mysticum

여섯 점이 한 개의 이차곡선 위에 있을 경우 60개의 서로 다른 방법의 육각형의 연결방법이 존재한다. 결과적으로 파스칼의 직선도 60개가 형성이 된다. 이 60개의 직선을 Hexagrammum Mysticum이라고 부른다.

토마스 커크만(Thomas Kirkman)은 1849년 이 60개의 직선이 60개의 점과 관련이 있다는 것을 보였다. 특히 각 직선은 이 관련 있는 점 세 개를 지나는 것도 보였다. 이 60개의 점을 커크만 점(Kirkman Points)라고 부른다.

증명

파스칼은 자신의 노트에서 증명방법을 적지 않았다. 하지만 다양한 증명방법이 있다.

부연설명

우선 증명방법에서 이차곡선이 원일 때만 보여도 충분하게 된다. 왜냐하면 모든 축퇴되지 않은(non-degenerate, 타원, 포물선, 쌍곡선을 포함한다) 이차곡선은 선형적 사영변환(projective transformation)에 의해 원으로 변환이 가능하기 때문이다.

우선 사영평면(Projective Plane) [math]\displaystyle{ \mathbb{P}^2 (k) }[/math]에 대해 체 k가 대수적으로 닫혀있다고 가정해도 된다. (algebraically closed) 왜냐하면 임의의 체는 대수적으로 닫힌 체 안에 들어가며, 교점의 개수가 최대일 때는 대수적으로 닫힌 체에서도 교점이 보존되기 때문이다.

[math]\displaystyle{ \mathbb{P}^2 (k) = \frac{k^3-(0,0,0)}{ \sim} }[/math]상에서 이차곡선(Conic section)의 공식은 [math]\displaystyle{ a x^2 + b y^2 + c z^2 + dxy + exz + fyz =0 }[/math]가 된다. 이것은 3×3 행렬을 이용해서 [math]\displaystyle{ \begin{bmatrix} x& y& z \end{bmatrix} \begin{bmatrix} a & d/2 & e/2 \\ d/2 & b & f/2 \\ e/2 & f/2 & c \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} }[/math]형태로 작성이 가능하다.

이 3X3 행렬은 대칭행렬이므로 직교행렬 P를 이용하면 [math]\displaystyle{ P \cdot \begin{bmatrix} a & d/2 & e/2 \\ d/2 & b & f/2 \\ e/2 & f/2 & c \end{bmatrix} \ P^t = \begin{bmatrix} A'& 0 & 0 \\ 0& B'& 0 \\ 0 & 0 & C'\end{bmatrix} }[/math]형태로 변환이 가능하다. 여기서 이차곡선은 축퇴(degenerated)되지 않으므로 A', B', C'의 값은 0이 되지 않는다. 한편 체 k는 대수적으로 닫힌 체(algebraically closed)이므로 [math]\displaystyle{ x^2-A'/B' =0, x^2 + A'/C' =0 }[/math]의 해는 항상 존재하며, 그 중에 한 해를 각각 [math]\displaystyle{ b', c' }[/math]라고 놓는다. (x,y,z)를 [math]\displaystyle{ \begin{bmatrix} x'\\ y'\\ z'\end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & b' & 0 \\ 0& 0& c'\end{bmatrix} \cdot P^t \begin{bmatrix} x \\ y \\ z \end{bmatrix} }[/math]로 변환시키면 [math]\displaystyle{ a x^2 + b y^2 + c z^2 + dxy + exz + fyz =0 }[/math] 식은 [math]\displaystyle{ {x'}^2 + {y'}^2 -{z'}^2 =0 }[/math]형태로 유도된다.

한편 선형변환 X는 일차식 [math]\displaystyle{ ax + by +cz=0 }[/math]을 다른 일차식 [math]\displaystyle{ a 'x + b'y + c'z =0 }[/math], [math]\displaystyle{ \begin{bmatrix} a'& b'& c'\end{bmatrix} = \begin{bmatrix} a& b& c\end{bmatrix} X }[/math]으로 변환시키기 때문에 한 직선은 선형변환에 의해서 다른 직선으로 변화하며, 따라서 공선점은 선형변환에 의해서 공선점으로 변한다. 임의의 축퇴되지 않는(Non-degenerated) 이차곡선은 대수적으로 닫힌 체의 선형변환에 의해서 원으로 변환이 가능한 것을 알 수 있다. 따라서 우리는 파스칼의 정리가 원에 대해서만 성립하는 것을 보여도 임의의 이차곡선에 대해 성립한다는 것을 보일 수 있다.

다만 파스칼의 정리는 일반적인 표현으로는 파푸스의 육각형 정리의 일반화된 정리이기는 하지만 이 방법을 사용할 수 있는 경우는 축퇴되지 않은(non-degenerated) 경우에 한정되므로 파푸스의 육각형 정리를 따름정리(Corollary)로 얻을 수 없다.

메넬라우스의 정리를 반복하는 방법

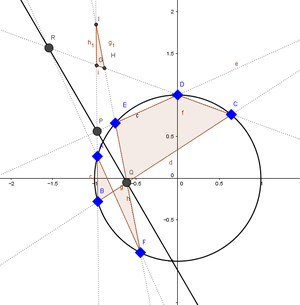
우선 위의 그림에서 AB와 DE의 교점 P, BC와 EF의 교점 Q, CD와 FA의 교점 R을 놓자. AB와 CD의 교점을 G, CD와 EF의 교점을 H, EF와 AB의 교점을 I라고 놓자. 그러면 삼각형 △GHI에 대해서 B, C, Q가 일직선상에 있으므로 메넬라우스의 정리를 적용하면 [math]\displaystyle{ \frac{IQ}{HQ} \frac{HC}{GC} \frac{GB}{IB} =1 }[/math]. (1)

마찬가지로 D, E, P가 일직선상에 있으므로 삼각형 △GHI에 대해 메넬라우스의 정리를 적용하면 [math]\displaystyle{ \frac{IE}{HE} \frac{HD}{GD} \frac{GP}{IP} =1 }[/math]. (2)

마찬가지로 A, F, R도 일직선상에 있으므로 삼각형 △GHI에 대해 메넬라우스의 정리를 적용하면 [math]\displaystyle{ \frac{GA}{IA} \frac{HR}{GR} \frac{IF}{HF} =1 }[/math]. (3)

한편 점 G, H, I와 원 위의 점 A, B, C, D, E, F에 의해 원주의 비례공식을 적용하면 [math]\displaystyle{ \frac{GA \cdot GB}{GC \cdot GD}=1 }[/math], [math]\displaystyle{ \frac{HC \cdot HD}{HE \cdot HF} =1 }[/math] , [math]\displaystyle{ \frac{IE \cdot IF}{IA \cdot IB} =1 }[/math]. (4)

(1)×(2)×(3)을 곱한 식은 [math]\displaystyle{ \frac{IQ}{HQ} \frac{HC}{GC} \frac{GB}{IB} \cdot \frac{IE}{HE} \frac{HD}{GD} \frac{GP}{IP} \cdot \frac{GA}{IA} \frac{HR}{GR} \frac{IF}{HF} }[/math] [math]\displaystyle{ = \frac{IQ}{HQ} \frac{GP}{IP}\frac{HR}{GR} \cdot \frac{GA \cdot GB}{GC \cdot GD} \cdot \frac{HC \cdot HD}{HE \cdot HF} \cdot \frac{IE \cdot IF}{IA \cdot IB} }[/math]

(4)를 이용하면 [math]\displaystyle{ = \frac{IQ}{HQ} \frac{GP}{IP}\frac{HR}{GR} =1 }[/math]. 메넬라우스의 정리를 이용하면 P, Q, R은 일직선상에 있다.

3차곡선을 이용한 증명방법

파스칼의 정리는 케일리-바하라흐 정리(Cayley-Bacharach Theorem)를 이용하면 엄청나게 간단하게 증명할 수 있다.^[2] 케일리-바카라치 정리는 대수적으로 닫힌 체 k와 사영공간 [math]\displaystyle{ \mathbb{P}^2 (k) }[/math]에 대해서 사영평면 안에서 8개의 임의의 점을 지나는 모든 3차곡선 [math]\displaystyle{ f(x,y)=0 }[/math]에 대해서 이 모든 곡선이 지나는 아홉 번째 점이 존재한다는 정리이다. 파스칼의 정리는 세 직선 AB, CD, EF를 0으로 보내는 삼차식 f₁과 BC, DE, FA를 0으로 보내는 삼차식 f₂가 주어지면, f₁=0과 f₂의 교점은 자연스럽게 A, B, C, D, E, F, P, Q, R이 된다. 케일리-바하라흐 정리를 이용하면 A, B, C, D, E, F, P, Q를 지나는 삼차곡선은 나머지 점 R을 반드시 지나게 된다. 특히 점 A, B, C, D, E, F가 이차곡선 위에 있으면 이 여덟 점을 지나는 삼차곡선은 P, Q를 지나는 일직선을 커버하게 된다. 따라서 R이 직선 PQ위에 존재하게 되고 증명이 완료되었다. 이 경우는 파푸스의 육각형 정리도 자연스럽게 증명된다.

참고로 케일리-바하라흐 정리는 3차 타원곡선 상에서의 연산자의 결합법칙을 증명하는 데에도 유용하다. 예를 들면 3차 타원곡선은 첫 번째 3개묶음의 직선 X₁, X₂, X₃와 Y₁, Y₂, Y₃에 대해서 [math]\displaystyle{ X_i \cap Y_j , i=1,2,3, j=1,2,3 }[/math]의 점 중 여덟 개를 지나는 삼차곡선이 반드시 나머지 한 점도 지나게 된다는 것을 보인다. 타원곡선에서 군(group)의 정의는 일직선 상에 있는 세 점의 곱은 항등원이 되게 정의하는데, 이 점을 이용하면 아래 그림처럼 결합법칙을 증명할 수 있게 된다.

파일:ElipticGroup.gif

베조의 정리(Bézout's theorem)를 이용하는 방법

우선 베조의 정리가 무엇인지 간단하게 살펴보자.

베조의 정리(Bézout's theorem) 복소수 상의 k차원 사영공간 [math]\displaystyle{ \mathbb{P}^k ( \mathbb{C}) }[/math]에 대해서 m₁차식 [math]\displaystyle{ f_1 (x_1 , \cdot\cdot\cdot, x_k)=0 }[/math], m₂차식 [math]\displaystyle{ f_2(x_1 , \cdot\cdot\cdot, x_k)=0 }[/math], ... m_r차식 [math]\displaystyle{ f_r (x_1 , \cdot\cdot\cdot, x_k) =0 }[/math]에 대해서 r≤k라고 가정하면 [math]\displaystyle{ \bigcap_{i\neq t}\left\{f_i=0\right\}\cap\left\{f_t=0\right\} }[/math]이 원래의 두 다원체의 차원(dimension)보다 떨어진다는 가정 하에서 교집합 [math]\displaystyle{ \bigcap_{i=1}^{r}\left\{f_i(x_1 , \cdots x_k)=0\right\} }[/math]은 최대한 [math]\displaystyle{ \prod_{i=1}^{r} m_i }[/math]차수로 구성된 k-r차원 대수적 사영다영체(projective variety)가 된다는 정리이다. 특히 k=r=2일때만 생각한다면 f의 차수를 m, g의 차수를 n으로 간주하면 연립방정식 [math]\displaystyle{ \begin{cases} f(x,y)=0 \\ g(x,y)=0 \end{cases} }[/math]에 대해서 k중근은 k개로 근으로 간주할 때 두 다항식의 영점이 다양체 하나를 통채로 공유하지 않는다면. 연립방정식을 만족하는 교점의 개수가 복소수 사영평면 안에서 정확히 mn개가 존재함을 의미한다.

삼차식 f가 직선 AB, CD, EF 위에서 함수값이 0이 되고, 삼차식 g가 직선 BC, DE, FA에서의 함수값이 0이 된다고 가정하자. 그렇다면 두 식의 영점의 교점인 A, B, C, D, E, F, P, Q, R을 얻을 수 있다. 일단 삼차식 h=f+λg로 놓으면 h=0도 f와 g의 교점 9개를 반드시 지나가게 된다. A, B, C, D, E, F를 지나는 이차곡선 위의 점 하나를 X로 잡고, 삼차식 h가 A, B, C, D, E, F, X를 지난다고 가정하하면 이차곡선 위에서 0이 되는 이차식 j에 대해서 h와 j의 교점은 7개가 된다. 베조의 정리에 의해서 h=0인 다양체(variety)가 j=0인 다양체를 포함하지 않는다면 {h=0}인 집합과 {j=0}인 집합은 기껏해야 3X2=6개의 점에서만 만나게 된다. 따라서 모순이 생기지 않기 위해서는 {h=0}이 반드시 {j=0}을 포함해야 한다는 것을 의미한다. 분명히 h는 이차곡선 바깥의 점 P, Q, R을 지나게 되므로 일차식 k가 있어서 {k=0}이 P, Q, R을 포함한다는 것을 의미한다. 따라서 h=0은 jk=0을 만족하고, 세 점 P, Q, R은 하나의 일차식의 영점이 되므로 일직선(파스칼 직선)상에 놓이게 되는 것을 알 수 있다.

파스칼의 육각형의 성질

위의 그림을 이용했을 때 우리는 아래와 같은 식이 성립합을 확인할 수 있다. ^[3]

[math]\displaystyle{ \frac{\overline{PB}}{\overline{PA}} \times \frac{\overline{RA}}{\overline{RF}} \times \frac{\overline{QF}}{\overline{QE}} \times\frac{\overline{PE}}{\overline{PD}} \times \frac{\overline{RD}}{\overline{RC}} \times \frac{\overline{QC}}{\overline{QB}}=1. }[/math]

바깥의 이차곡선이 원일 때에는 원주의 성질을 이용하면 쉽게 유도가 가능하지만 원이 아닐 경우에는 직접 보이기에는 굉장히 까다롭다. 자세한 내용은 해당 웹사이트를 참조하자.

파스칼의 육각형의 축퇴형(degeneration)

파스칼의 육각형은 한 변이 한 점으로 축퇴(degenerating)됨에 따라서 육각형 대신 오각형, 사각형, 삼각형과 원의 접선에 대한 정리로 표현할 수 있다. 이미지

출처

Biggs, N. L. (1981), "T. P. Kirkman, mathematician", The Bulletin of the London Mathematical Society 13 (2): 97–120, doi:10.1112/blms/13.2.97, MR 608093

Coxeter, H. S. M.; Greitzer, S. L. (1967), Geometry Revisited, Washington, DC: Mathematical Association of America, p. 76

Guggenheimer, Heinrich W. (1967), Plane geometry and its groups, San Francisco, Calif.: Holden–Day Inc., MR 0213943
Mills, Stella (March 1984), "Note on the Braikenridge–Maclaurin Theorem", Notes and Records of the Royal Society of London (The Royal Society) 38 (2): 235–240, doi:10.1098/rsnr.1984.0014, JSTOR 531819
Modenov, P.S.; Parkhomenko, A.S. (2001), "P/p071780", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Pascal, Blaise (1640). "Essay pour les coniques" (facsimile). Niedersächsiche Landesbibliothek, Gottfried Wilhelm Leibniz Bibliothek. Retrieved 21 June 2013.
Smith, David Eugene (1959), A Source Book in Mathematics, New York: Dover, ISBN 0-486-64690-4

Stefanovic, Nedeljko (2010), A very simple proof of Pascal's hexagon theorem and some applications (PDF), Indian Academy of Sciences Wells, David (1991), The Penguin Dictionary of Curious and Interesting Geometry, London: Penguin Books, ISBN 0-14-011813-6

Young, John Wesley (1930), Projective Geometry, The Carus Mathematical Monographs, Number Four, The Mathematical Association of America
van Yzeren, Jan (1993), "A simple proof of Pascal's hexagon theorem", The American Mathematical Monthly (Mathematical Association of America) 100 (10): 930–931, doi:10.2307/2324214, ISSN 0002-9890, JSTOR 2324214, MR 1252929

외부 링크

Interactive demo of Pascal's theorem (Java required) at cut-the-knot
60 Pascal Lines (Java required) at cut-the-knot
The Complete Pascal Figure Graphically Presented by J. Chris Fisher and Norma Fuller (University of Regina)
Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes (PDF; 891 kB), Uni Darmstadt, S. 29-35.

각주

↑ 이것은 원이나 타원처럼 닫힌 이차곡선에 외접하는 육각형에 대해 맞은편 꼭지점을 연결한 세 대각선이 한 점에 만난다는 것을 보이는 정리이다.
↑ 이 정리 자체에 대한 증명은 이곳을 참조
↑ A Property of Pascal's Hexagon Pascal May Have Overlooked (2014년 2월 3일).

이 문서에는 영어판 위키백과의 Pascal's Theorem 문서 709338064 판을 번역한 내용이 포함되어 있습니다.

[1] 이것은 원이나 타원처럼 닫힌 이차곡선에 외접하는 육각형에 대해 맞은편 꼭지점을 연결한 세 대각선이 한 점에 만난다는 것을 보이는 정리이다.

[2] 이 정리 자체에 대한 증명은 이곳을 참조

[3] A Property of Pascal's Hexagon Pascal May Have Overlooked (2014년 2월 3일).

[1]

[2]

[3]