Junseong26 (토론 | 기여) (새 문서: {{학술}} 분류:물리학 독일 천문학자 케플러는 그의 스승인 브라헤가 죽기 직전 짧은 기간동안 브라헤의 조수였는데, 스승의 자료를 받...) |
잔글편집 요약 없음 |
||
| 2번째 줄: | 2번째 줄: | ||
[[분류:물리학]] | [[분류:물리학]] | ||
독일의 천문학자 [[요하네스 케플러]]가 [[티코 브라헤]]의 자료를 받아 16년만에 정립한 행성들의 움직임에 관한 법칙. | |||
보통 다음의 세 가지로 표현된다. | |||
==케플러의 제1법칙== | ==케플러의 제1법칙== | ||
[[파일:대학물리학I그림13.4.png|섬네일|오른쪽]] | [[파일:대학물리학I그림13.4.png|섬네일|오른쪽]] | ||
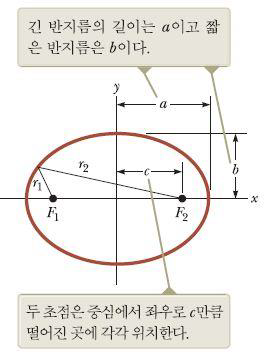
{{인용문|1. 모든 행성들은 태양을 한 초점으로 하는 타원 궤도를 따라서 이동한다.}} | |||
거리 제곱에 반비례하는 중력의 성질의 결과이다. | |||
특히, 두 초점이 일치하는 타원의 경우 원이 된다. | |||
==케플러의 제2법칙== | ==케플러의 제2법칙== | ||
[[파일:대학물리학I그림13.6.png|섬네일|오른쪽]] | [[파일:대학물리학I그림13.6.png|섬네일|오른쪽]] | ||
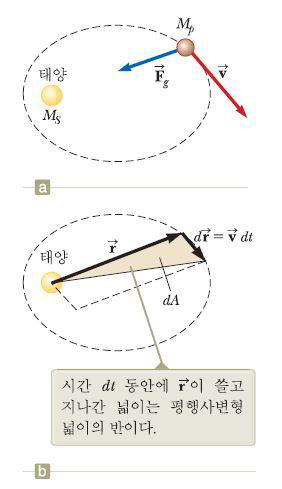
{{인용문|2. 태양과 행성을 잇는 반지름 벡터는 같은 시간 간격 동안에 같은 넓이를 쓸고 지나간다.}} | |||
각운동량 보존의 결과로 설명할 수 있다. 태양이 행성에 비해 훨씬 더 큰 질량을 가지고 있으면, 태양은 움직이지 않는다고 가정한다. 태양이 행성에 작용하는 중력은 중심력이며, 태양을 향하는 반지름 방향이다. | 각운동량 보존의 결과로 설명할 수 있다. 태양이 행성에 비해 훨씬 더 큰 질량을 가지고 있으면, 태양은 움직이지 않는다고 가정한다. 태양이 행성에 작용하는 중력은 중심력이며, 태양을 향하는 반지름 방향이다. | ||
| 33번째 줄: | 35번째 줄: | ||
==케플러의 제3법칙== | ==케플러의 제3법칙== | ||
{{인용문|3. 모든 행성의 궤도 주기의 제곱은 그 행성 궤도의 긴 반지름의 세제곱에 비례한다.}} | |||
행성이 원운동할 때 행성의 구심 가속도를 제공하는 것이 중력이므로, 등속 원운동을 하는 물체에 뉴턴의 제2법칙을 적용하면 | 행성이 원운동할 때 행성의 구심 가속도를 제공하는 것이 중력이므로, 등속 원운동을 하는 물체에 뉴턴의 제2법칙을 적용하면 | ||
2015년 7월 9일 (목) 23:12 판
독일의 천문학자 요하네스 케플러가 티코 브라헤의 자료를 받아 16년만에 정립한 행성들의 움직임에 관한 법칙.
보통 다음의 세 가지로 표현된다.
케플러의 제1법칙
“ 1. 모든 행성들은 태양을 한 초점으로 하는 타원 궤도를 따라서 이동한다. “
거리 제곱에 반비례하는 중력의 성질의 결과이다.
특히, 두 초점이 일치하는 타원의 경우 원이 된다.
케플러의 제2법칙
“ 2. 태양과 행성을 잇는 반지름 벡터는 같은 시간 간격 동안에 같은 넓이를 쓸고 지나간다. “
각운동량 보존의 결과로 설명할 수 있다. 태양이 행성에 비해 훨씬 더 큰 질량을 가지고 있으면, 태양은 움직이지 않는다고 가정한다. 태양이 행성에 작용하는 중력은 중심력이며, 태양을 향하는 반지름 방향이다.
[math]\displaystyle{ \tau = r\times {F}_{g} = 0 }[/math]
[math]\displaystyle{ L = r\times p = {M}_{p}r\times v = }[/math] 일정
그림 b에서 반지름 벡터 [math]\displaystyle{ \vec{r} }[/math]은 시간 dt동안 넓이 dA를 쓸고 지나가는데 이 넓이는 벡터 [math]\displaystyle{ \vec{r} }[/math]과 [math]\displaystyle{ d\vec{r} }[/math]이 만든 평행사변형의 넓이 [math]\displaystyle{ \left|\vec{r}\times d\vec{r} \right| }[/math]의 반이다. 시간 dt동안 행성이 지나간 거리는 [math]\displaystyle{ d\vec{r} = \vec{v}dt }[/math]이므로
[math]\displaystyle{ dA = \frac{1}{2}\left|\vec{r}\times d\vec{r} \right| = \frac{1}{2}\left|\vec{r}\times \vec{v}dt \right| = \frac{L}{{2M}_{p}dt} }[/math]
[math]\displaystyle{ \frac{dA}{dt} = \frac{L}{{2M}_{p}} }[/math]
여기서 L과 Mp는 모두 상수이다.
케플러의 제3법칙
“ 3. 모든 행성의 궤도 주기의 제곱은 그 행성 궤도의 긴 반지름의 세제곱에 비례한다. “
행성이 원운동할 때 행성의 구심 가속도를 제공하는 것이 중력이므로, 등속 원운동을 하는 물체에 뉴턴의 제2법칙을 적용하면
[math]\displaystyle{ {F}_{g} = \frac{G{M}_{s}{M}_{p}}{{r}^{2}} = {M}_{p}a = \frac{{M}_{p}{v}^{2}}{r} }[/math]
[math]\displaystyle{ v = \frac{2\pi r}{T} }[/math](T:주기)이므로
[math]\displaystyle{ \frac{G{M}_{s}}{{r}^{2}} = \frac{\left(2\pi r/T \right)}{r} }[/math]
[math]\displaystyle{ {T}^{2} = \left(\frac{4{\pi }^{2}}{G{M}_{s}} \right){r}^{3} = {K}_{s}{r}^{3} }[/math]
타원 궤도인 경우에는 r을 긴 반지름 a로 바꾸면 된다.
[math]\displaystyle{ {T}^{2} = \left(\frac{4{\pi }^{2}}{G{M}_{s}} \right){a}^{3} = {K}_{s}{a}^{3} }[/math]