삼각함수의 덧셈정리

개요

[math]\displaystyle{ \sin75^\circ }[/math]의 값은 뭘까? 만약 삼각함수가 선형 함수라면 [math]\displaystyle{ \sin75^\circ=\sin45^\circ+\sin30^\circ=\frac{\sqrt2}{2}+\frac{1}{2}=\frac{1+\sqrt{2}}{2} }[/math]일 것이다. 하지만 실제 값은 [math]\displaystyle{ \frac{\sqrt{6}+\sqrt{2}}{4} }[/math]로, 좀 많이 다르다. 삼각함수의 덧셈정리는 이런 문제를 풀기 위해 만들어진 공식으로, 안그래도 많고 복잡한 삼각함수의 공식을 두 배로 불려주는 역할을 담당한다.

덧셈정리

전부 복부호동순이다.

• [math]\displaystyle{ \sin\left(\alpha\pm\beta\right)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta }[/math]
• [math]\displaystyle{ \cos\left(\alpha\pm\beta\right)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta }[/math]
• [math]\displaystyle{ \tan\left(\alpha\pm\beta\right)=\frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta} }[/math]

증명

여러가지 증명 방법이 있지만 벡터를 사용하는 것이 가장 일반적이다. 일반각에 대해 증명이 가능하기 때문.

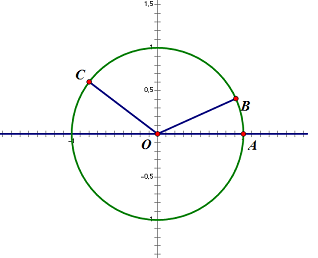
두 벡터 [math]\displaystyle{ \vec{OB}, \vec{OC} }[/math]의 내적을 구하면, [math]\displaystyle{ \vec{OC}\cdot\vec{OB}=\left|\vec{OC}\right|\cdot\left|\vec{OB}\right|\cos\left(\angle COB\right)=1\cdot1\cdot\cos\left(\alpha-\beta\right) }[/math]. 한편 두 벡터의 내적을 성분으로 나타내면, [math]\displaystyle{ \vec{OC}\cdot\vec{OB}=\left(\cos\alpha, \sin\alpha\right)\cdot\left(\cos\beta, \sin\beta\right)=\cos\alpha\cos\beta+\sin\alpha\sin\beta }[/math]. 따라서 [math]\displaystyle{ \cos\left(\alpha-\beta\right)=\cos\alpha\cos\beta+\sin\alpha\sin\beta }[/math].

벡터를 모르더라도 단위원과 코사인 법칙을 사용하여 증명이 가능하다.

단위원의 중심을 O, 양의 x축을 시초선으로하고 각의 크기가 각각 [math]\displaystyle{ \beta, \alpha }[/math]인 동경이 단위원과 만나는 점을 각각 [math]\displaystyle{ B, C }[/math]라고 하자 (즉, [math]\displaystyle{ \angle AOB=\beta, \angle AOC=\alpha }[/math]). 그럼 두 점의 좌표는 [math]\displaystyle{ B\left(\cos\beta, \sin\beta\right), C\left(\cos\alpha, \sin\alpha\right) }[/math]이다. 두 점 사이의 거리를 구하는 공식으로 부터, [math]\displaystyle{ \overline{BC}^2=\left(\cos\beta-\cos\alpha\right)^2+\left(\sin\beta-\sin\alpha\right)^2=\left(\cos^2\alpha+\sin^2\alpha\right)+\left(\cos^2\beta+\sin^2\beta\right)-2\left(\cos\beta\cos\alpha+\sin\beta\sin\alpha\right)= }[/math]
[math]\displaystyle{ 2-\left(\cos\beta\cos\alpha+\sin\beta\sin\alpha\right) }[/math]. 한편, 코사인법칙으로부터, [math]\displaystyle{ \overline{BC}^2=1^2+1^2-2\cdot1\cdot1\cdot\cos\left(\alpha-\beta\right) }[/math]이다. 따라서, [math]\displaystyle{ \cos\left(\alpha-\beta\right)=\cos\alpha\cos\beta+\sin\alpha\sin\beta }[/math].

위 두 증명에서는 공통적으로 코사인에 대한 덧셈정리만을 증명했는데, 나머지 부분의 증명은 다음과 같다.

[math]\displaystyle{ \cos\left(\alpha-\beta\right)=\cos\alpha\cos\beta+\sin\alpha\sin\beta }[/math]의 [math]\displaystyle{ \beta }[/math]에 [math]\displaystyle{ -\beta }[/math]를 대입하면 [math]\displaystyle{ \cos\left(\alpha+\beta\right)=\cos\alpha\cos\beta-\sin\alpha\sin\beta }[/math].

한편, [math]\displaystyle{ \sin\left(\alpha+\beta\right)=\cos\left(\frac{\pi}{2}-\left(\alpha+\beta\right)\right)=\cos\left(\left(\frac{\pi}{2}-\alpha\right)-\beta\right)= }[/math]
[math]\displaystyle{ \cos\left(\frac{\pi}{2}-\alpha\right)\cos\beta+\sin\left(\frac{\pi}{2}-\alpha\right)\sin\beta=\sin\alpha\cos\beta+\cos\alpha\sin\beta }[/math]. 여기서 [math]\displaystyle{ \beta }[/math]에 [math]\displaystyle{ -\beta }[/math]를 대입하면 [math]\displaystyle{ \sin\left(\alpha-\beta\right)=\sin\alpha\cos\beta-\cos\alpha\sin\beta }[/math].

마지막으로, [math]\displaystyle{ \tan\left(\alpha+\beta\right)=\frac{\sin\left(\alpha+\beta\right)}{\cos\left(\alpha+\beta\right)}=\frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta} }[/math]. 여기서 분자, 분모를 [math]\displaystyle{ \cos\alpha\cos\beta }[/math]로 나누면 [math]\displaystyle{ \tan\left(\alpha+\beta\right)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} }[/math]. 여기서 [math]\displaystyle{ \beta }[/math]에 [math]\displaystyle{ -\beta }[/math]를 대입하면 [math]\displaystyle{ \tan\left(\alpha-\beta\right)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} }[/math].

삼각함수의 합성

삼각함수의 덧셈정리를 응용해서 [math]\displaystyle{ a\sin\theta+b\cos\theta }[/math]형태로 나타난 삼각함수를 아래와 같이 하나로 합칠 수 있다.

1. [math]\displaystyle{ a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin\left(\theta+\alpha\right),\, \left(\cos\alpha=\frac{a}{\sqrt{a^2+b^2}},\sin\alpha=\frac{b}{\sqrt{a^2+b^2}}\right) }[/math]
2. [math]\displaystyle{ a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\cos\left(\theta-\beta\right), \, \left(\cos\beta=\frac{b}{\sqrt{a^2+b^2}}, \sin\beta=\frac{a}{\sqrt{a^2+b^2}}\right) }[/math]
3. 최댓값: [math]\displaystyle{ \sqrt{a^2+b^2} }[/math], 최솟값: [math]\displaystyle{ -\sqrt{a^2+b^2} }[/math], 주기: [math]\displaystyle{ 2\pi }[/math]

증명은 그림을 그려서 각 [math]\displaystyle{ \alpha }[/math]나 [math]\displaystyle{ \beta }[/math]를 찾아서 합성하거나, 아니면 우변에 있는 합성된 삼각함수를 덧셈정리로 풀어서 정리하면 된다.

배각, 반각 공식

삼각함수의 덧셈정리에서 두 각을 같게 놔두면 2배각의 공식을 만들 수 있다.

1. [math]\displaystyle{ \sin 2\alpha=2\sin\alpha\cos\alpha }[/math]
2. [math]\displaystyle{ \cos 2\alpha=\cos^2\alpha-\sin^2\alpha=2\cos^2\alpha-1=1-2\sin^2\alpha }[/math]
3. [math]\displaystyle{ \tan 2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha} }[/math]

특히 코사인의 2배각 공식은 3가지 형태가 있는데, [math]\displaystyle{ \sin^2\alpha+\cos^2\alpha=1 }[/math]를 이용해서 변형한 것이다.

덧셈정리에서 두각을 [math]\displaystyle{ \alpha, 2\alpha }[/math]로 놔두면 3배각의 공식을 만들 수 있다.

1. [math]\displaystyle{ \sin 3\alpha=3\sin\alpha-4\sin^3\alpha }[/math]
2. [math]\displaystyle{ \cos 3\alpha=4\cos^3\alpha-3\cos\alpha }[/math]

증명은 덧셈정리를 이용해서 쭉 풀어나가면 된다.

또한, 코사인의 2배각 공식에서 반각 공식을 유도할 수 있다.[math]\displaystyle{ \alpha }[/math]대신 [math]\displaystyle{ \alpha/2 }[/math]를 대입하면 된다.

1. [math]\displaystyle{ \sin^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{2} }[/math]
2. [math]\displaystyle{ \cos^2\frac{\alpha}{2}=\frac{1+\cos\alpha}{2} }[/math]
3. [math]\displaystyle{ \tan^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{1+\cos\alpha} }[/math]

삼각함수의 합차공식

삼각함수의 덧셈정리에서 유도되는 공식들. 으아아아 제발 그만 다 외워도 상관은 없지만 유도 방법을 안 뒤, 필요할 때마다 유도하는 것이 좋다. 사실 덧셈정리와 어느 정도 유사성이 있기 때문에 통째로 외우는 것이 그렇게 어려운 것은 아니다.

증명의 편의를 위해 덧셈정리에 번호를 매기도록 하겠다.

1. [math]\displaystyle{ \sin\left(\alpha+\beta\right)=\sin\alpha\cos\beta+\cos\alpha\sin\beta }[/math]
2. [math]\displaystyle{ \sin\left(\alpha-\beta\right)=\sin\alpha\cos\beta-\cos\alpha\sin\beta }[/math]
3. [math]\displaystyle{ \cos\left(\alpha+\beta\right)=\cos\alpha\cos\beta-\sin\alpha\sin\beta }[/math]
4. [math]\displaystyle{ \cos\left(\alpha-\beta\right)=\cos\alpha\cos\beta+\sin\alpha\sin\beta }[/math]

곱을 합차로 바꾸는 공식

1번식과 2번식을 더한뒤 2로 나누면, [math]\displaystyle{ \sin\alpha\cos\beta=\frac{1}{2}\left(\sin\left(\alpha+\beta\right)+\sin\left(\alpha-\beta\right)\right) }[/math].

1번식에서 2번식을 뺀뒤 2로 나누면, [math]\displaystyle{ \cos\alpha\sin\beta=\frac{1}{2}\left(\sin\left(\alpha+\beta\right)-\sin\left(\alpha-\beta\right)\right) }[/math].

3번식과 4번식을 더한뒤 2로 나누면, [math]\displaystyle{ \cos\alpha\cos\beta=\frac{1}{2}\left(\cos\left(\alpha+\beta\right)+\cos\left(\alpha-\beta\right)\right) }[/math].

3번식에서 4번식을 뺀뒤 2로 나누면, [math]\displaystyle{ \sin\alpha\sin\beta=-\frac{1}{2}\left(\cos\left(\alpha+\beta\right)-\cos\left(\alpha-\beta\right)\right) }[/math].

합차를 곱으로 바꾸는 공식

바로 윗문단의 공식에서 유도되는 또 다른 공식. [math]\displaystyle{ \alpha+\beta=A, \alpha-\beta=B }[/math]로 치환한뒤 [math]\displaystyle{ \alpha, \beta }[/math]에 관해서 풀면, [math]\displaystyle{ \alpha=\frac{A+B}{2}, \beta=\frac{A-B}{2} }[/math]이고, 이 값을 식에 대입한 뒤 좌변과 우변을 바꾸면 아래 공식을 얻는다.

1. [math]\displaystyle{ \sin A+\sin B=2\sin\frac{A+B}{2}\cos\frac{A-B}{2} }[/math]
2. [math]\displaystyle{ \sin A-\sin B=2\cos\frac{A+B}{2}\sin\frac{A-B}{2} }[/math]
3. [math]\displaystyle{ \cos A+\cos B=2\cos\frac{A+B}{2}\cos\frac{A-B}{2} }[/math]
4. [math]\displaystyle{ \cos A-\cos B=-2\sin\frac{A+B}{2}\sin\frac{A-B}{2} }[/math]

정리

덧셈정리에서 유도되는 수많은 공식들을 표로 정리하면 다음과 같다.

분류	공식
덧셈정리	[math]\displaystyle{ \sin\left(\alpha\pm\beta\right)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta }[/math]
	[math]\displaystyle{ \cos\left(\alpha\pm\beta\right)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta }[/math]
	[math]\displaystyle{ \tan\left(\alpha\pm\beta\right)=\frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta} }[/math]
합성	[math]\displaystyle{ \sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin\left(\theta+\alpha\right),\, \left(\cos\alpha=\frac{a}{\sqrt{a^2+b^2}},\sin\alpha=\frac{b}{\sqrt{a^2+b^2}}\right) }[/math]
	[math]\displaystyle{ \sin\theta+b\cos\theta=\sqrt{a^2+b^2}\cos\left(\theta-\beta\right), \, \left(\cos\beta=\frac{b}{\sqrt{a^2+b^2}}, \sin\beta=\frac{a}{\sqrt{a^2+b^2}}\right) }[/math]
2배각	[math]\displaystyle{ \sin 2\alpha=2\sin\alpha\cos\alpha }[/math]
	[math]\displaystyle{ \cos 2\alpha=\cos^2\alpha-\sin^2\alpha=2\cos^2\alpha-1=1-2\sin^2\alpha }[/math]
	[math]\displaystyle{ \tan 2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha} }[/math]
3배각	[math]\displaystyle{ \sin 3\alpha=3\sin\alpha-4\sin^3\alpha }[/math]
	[math]\displaystyle{ \cos 3\alpha=4\cos^3\alpha-3\cos\alpha }[/math]
반각	[math]\displaystyle{ \sin^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{2} }[/math]
	[math]\displaystyle{ \cos^2\frac{\alpha}{2}=\frac{1+\cos\alpha}{2} }[/math]
	[math]\displaystyle{ \tan^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{1+\cos\alpha} }[/math]
곱을 합차로	[math]\displaystyle{ \sin\alpha\cos\beta=\frac{1}{2}\left(\sin\left(\alpha+\beta\right)+\sin\left(\alpha-\beta\right)\right) }[/math]
	[math]\displaystyle{ \cos\alpha\sin\beta=\frac{1}{2}\left(\sin\left(\alpha+\beta\right)-\sin\left(\alpha-\beta\right)\right) }[/math]
	[math]\displaystyle{ \cos\alpha\cos\beta=\frac{1}{2}\left(\cos\left(\alpha+\beta\right)+\cos\left(\alpha-\beta\right)\right) }[/math]
	[math]\displaystyle{ \sin\alpha\sin\beta=-\frac{1}{2}\left(\cos\left(\alpha+\beta\right)-\cos\left(\alpha-\beta\right)\right) }[/math]
합차를 곱으로	[math]\displaystyle{ \sin A+\sin B=2\sin\frac{A+B}{2}\cos\frac{A-B}{2} }[/math]
	[math]\displaystyle{ \sin A-\sin B=2\cos\frac{A+B}{2}\sin\frac{A-B}{2} }[/math]
	[math]\displaystyle{ \cos A+\cos B=2\cos\frac{A+B}{2}\cos\frac{A-B}{2} }[/math]
	[math]\displaystyle{ \cos A-\cos B=-2\sin\frac{A+B}{2}\sin\frac{A-B}{2} }[/math]

뭐가 이렇게 많아

외우는 요령

그런거 없다

사실 모든 공식을 외우는 것 보다는 모든 공식을 유도할 수 있는 것이 더 중요하다. 하지만 제한된 시간 안에 문제를 풀어야 하는 학교 시험같은 곳에서는 필요할 때마다 일일이 유도할 수 없는 노릇이니 어느 정도 암기가 필요하다. 아래는 위 수많은 공식의 암기 방법 중 하나. 만약 아래 방법이 자신에게 맞지 않는다면 자신만의 방법을 찾아보자.

• 덧셈 정리: 기본 중의 기본. 덧셈 정리를 못 외우면 유도되는 공식들을 전부 못 외운다 봐도 무방하다. 외울 때는 사코코사, 코코마사사, 일마타타타플타으로 외우는 방법이 있다. 보면 알겠지만, 사는 사인, 코는 코사인, 타는 탄젠트, 마는 마이너스, 플은 플러스를 뜻한다.
• 배각 공식: 사인은 두사코, 코사인은 코제마사제로 바꾸면 된다. 여기서 제는 당연히 제곱을 뜻한다. 코사인의 배각 공식의 경우는 총 세 가지가 있는데, "코제마사제"에서 아주 간단하게 유도되니 따로 외워 줄 필요는 없다. 만약 외우고 싶다면, 사인은 마이너스와, 코사인은 플러스와 연관되어 있다고만 생각해주자.
• 3배각 공식: 사인은 343, 코사인은 433. 뭔소린가 하면, 4 뒤의 3은 세제곱을, 나머지 숫자는 계수를 말한다. 여기서도 사인은 마이너스와, 코사인은 플러스와 연관되어 있다.
• 반각 공식: 간단하기 때문에 큰 문제는 없다. 부호가 헷갈린다면 사인은 마이너스, 코사인은 플러스와 관련있다고 생각해주자.
• 곱을 합차로: 믿기 힘들겠지만, 공식 4개를 통째로 외우는 것이 쉽다. 등호 좌변을 읽어 보면 사코코사코코사사인데, 이는 덧셈 정리의 그것과 형태가 같다. 등호 우변은 사사사사코코코코라 외우기 더 쉽다. 중간의 부호는 플마플마, 계수는 1/2. 마지막 줄은 마이너스를 앞에 곱해야 하는데, 좌변의 코코마사사에서 마가 오른쪽으로 옮겨 갔다 생각하자. 각도는 합차 공식이므로 합차가 번갈아 나온다고 생각하자.
• 합차를 곱으로: 이것 역시 공식 4개를 통째로 외우는 것이 쉽다. 등호 좌변은 사사사사코코코코, 우변은 사코코사코코사사, 좌변의 중간 부호는 플마플마, 우변의 계수는 2. 마지막 줄 역시 마이너스를 앞에 곱해야 하는데, 이 역시 코코마사사에서 마가 옮겨 갔다 생각하면 된다. 각도의 경우는 합차가 번갈아 나오는데, 절반으로 나눠줘야 한다. 식 앞에 계수 2가 있기 때문에 절반으로 나눈다 생각하면 된다.
• 합성: 그냥 유도하자. 시험에 잘 안나온다.

관련 항목

• 삼각함수