편집 요약 없음 |
태그: 일괄 되돌리기 |
||
| (사용자 3명의 중간 판 16개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
변심거리(邊心距離,apothem 또는 줄여서 apo)또는 '정다각형의 변심거리'는 [[기하학]]에서 [[정다각형]]의 중심에서 [[변]]까지의 거리를 말한다. | 변심거리(邊心距離,apothem 또는 줄여서 apo)또는 '정다각형의 변심거리'는 [[기하학]]에서 [[정다각형]]의 중심에서 [[변]]까지의 거리를 말한다. | ||
또는 원의 중심을 지나는 직선이 현을 수직이등분할때 중심부터 현까지의 거리를 말한다. | |||
==정사각형== | ==정사각형== | ||
[[원 (도형) |원]]에 내접한 정다각형의 변심거리(apo)는 연장선상의 [[화살거리]](sagit)와 더해져 [[반지름]]이 된다. | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| align='center'|[[파일: | | align='center'|[[파일:apothem sagit.svg|350px]] | ||
|- | |- | ||
| 원에 내접한 정사각형의 한변에 도달한 변심거리와 원의 반지름 그리고 그 둘의 간격 차인 화살거리 | | 원에 내접한 정사각형의 한변에 도달한 변심거리와 원의 반지름 그리고 그 둘의 간격 차인 화살거리 | ||
| 11번째 줄: | 13번째 줄: | ||
==현== | ==현== | ||
변심거리의 변을 | 변심거리의 변을 [[현 (수학)|현]]으로 가정해볼때 현을 수직이등분하는 직선이 원의 중심을 지나는것과 관련있음을 확인할수있다. <ref>[참고] (수학방 -원의 방정식,원의 방정식 표준형) https://mathbang.net/454</ref><ref>우리말샘 원 등</ref> 또한 직경과 현의 길이와의 관계는 [[피타고라스의 정리]]를 통해서 조사할수있다. | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| align='center'|[[파일: | | align='center'|[[파일:Euclid Elements 3-35.svg|400px]] | ||
|- | |- | ||
| [[유클리드 기하학 원론]] 제3권 법칙35 | | [[유클리드 기하학 원론]] 제3권 법칙35 | ||
| 20번째 줄: | 22번째 줄: | ||
현 <math> \overline{CD} </math>와 직경<math> \overline{AB} </math>가 수직으로 만나는 점 E에서 선분 AE와 선분EB와의 비율은 원둘레에서 호의 길이의 비율을 보여준다. | 현 <math> \overline{CD} </math>와 직경<math> \overline{AB} </math>가 수직으로 만나는 점 E에서 선분 AE와 선분EB와의 비율은 원둘레에서 호의 길이의 비율을 보여준다. | ||
따라서 이러한 성질은 선분 AE와 선분EB와의 비율에서 역시 [[활꼴]]의 면적을 보여줄 수 있다. | 따라서 이러한 성질은 선분 AE와 선분EB와의 비율에서 역시 [[활꼴]]의 면적을 보여줄 수 있다. | ||
:<math> \overline{AB} </math>가 원의 중심을 지나 현 <math> \overline{CD} </math>를 [[수직이등분]]할때 | |||
:<math> \overline{OC}^2 = \overline{CE}^2+ \overline{OE}^2 </math> | |||
:<math> \overline{OC} = \overline{OB} = \overline{AO} </math> | |||
:<math> \overline{OB}= \overline{OE} + \overline{EB}</math> | |||
따라서 | |||
:<math> \overline{CE}^2 =\overline{OC}^2 - \overline{OE}^2 </math> | |||
:<math> \overline{CE}^2 =\overline{AO}^2 - \overline{OE}^2 </math> | |||
그리고 | |||
:<math>\overline{AO}^2 - \overline{OE}^2 = \left( \overline{AO} -\overline{OE}\right) \left(\overline{AO}+ \overline{OE} \right)</math> | |||
:<math>\overline{AO}^2 - \overline{OE}^2 = \left( \overline{EB}\right) \left(\overline{AE} \right)</math> | |||
따라서 | |||
:<math> \left( \overline{CE}\right) \left(\overline{CE} \right) =\left( \overline{EB}\right) \left(\overline{AE} \right)</math> | |||
:<math> \left( \overline{CE}\right) \left(\overline{ED} \right) =\left( \overline{EB}\right) \left(\overline{AE} \right)</math>이다. | |||
이렇게 현의 길이와 직경(지름)의 길이는 일대일 대응한다.<br /> | |||
한편 활꼴의 길이 선분CD와 활꼴의 높이 선분EB를 갖는 활꼴의 길이(<math>l</math>)는 높이(<math> h</math>)와 직경(<math>D</math>)에서 다음의 관계가 있다. | 한편 활꼴의 길이 선분CD와 활꼴의 높이 선분EB를 갖는 활꼴의 길이(<math>l</math>)는 높이(<math> h</math>)와 직경(<math>D</math>)에서 다음의 관계가 있다. | ||
:<math> \left( \overline{CE} \right) \left( \overline{ED} \right) = \left( \overline{AE} \right) \left( \overline{EB} \right) </math>이다. | :<math> \left( \overline{CE} \right) \left( \overline{ED} \right) = \left( \overline{AE} \right) \left( \overline{EB} \right) </math>이다. | ||
| 31번째 줄: | 46번째 줄: | ||
:<math> l = 2\sqrt{(D-b)b}</math> | :<math> l = 2\sqrt{(D-b)b}</math> | ||
따라서 | 따라서 | ||
:<math> l = 2\sqrt{(D-b)b} = \sqrt{4} \sqrt{(D-h)h}</math> | :<math> l = 2\sqrt{(D-b)b} </math> | ||
:<math> l = \sqrt{4} \sqrt{(D-h)h}</math> | |||
:<math> l = \sqrt{ \left( 4D h \right) - \left( 4 h^2 \right) }</math> | :<math> l = \sqrt{ \left( 4D h \right) - \left( 4 h^2 \right) }</math> | ||
| 37번째 줄: | 53번째 줄: | ||
*[[부채꼴]] | *[[부채꼴]] | ||
<hr> | <hr> | ||
*[참고](유클리드 기하학 원론,구텐베르크 프로젝트,John Casey 1885)http://www.gutenberg.org/files/21076/21076-pdf.pdf?session_id=9bfd9ef535a37ac859a6028f101fa4451e3226cc | |||
[[분류:기하학]] | [[분류:기하학]] | ||
2024년 4월 11일 (목) 18:41 기준 최신판
변심거리(邊心距離,apothem 또는 줄여서 apo)또는 '정다각형의 변심거리'는 기하학에서 정다각형의 중심에서 변까지의 거리를 말한다.
또는 원의 중심을 지나는 직선이 현을 수직이등분할때 중심부터 현까지의 거리를 말한다.
정사각형[편집 | 원본 편집]
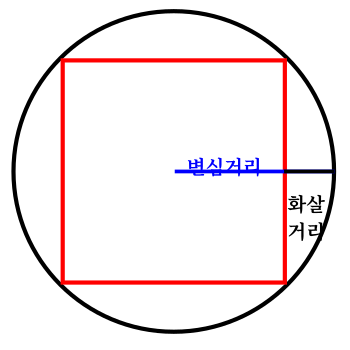
원에 내접한 정다각형의 변심거리(apo)는 연장선상의 화살거리(sagit)와 더해져 반지름이 된다.
|
| 원에 내접한 정사각형의 한변에 도달한 변심거리와 원의 반지름 그리고 그 둘의 간격 차인 화살거리 |
현[편집 | 원본 편집]
변심거리의 변을 현으로 가정해볼때 현을 수직이등분하는 직선이 원의 중심을 지나는것과 관련있음을 확인할수있다. [1][2] 또한 직경과 현의 길이와의 관계는 피타고라스의 정리를 통해서 조사할수있다.
|
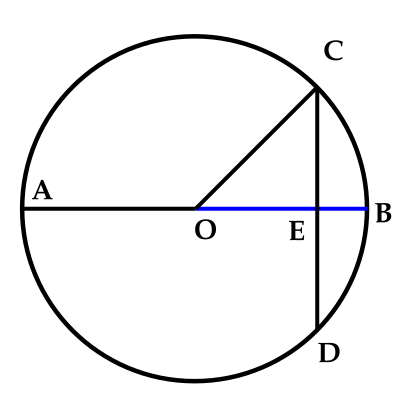
| 유클리드 기하학 원론 제3권 법칙35 |
현 [math]\displaystyle{ \overline{CD} }[/math]와 직경[math]\displaystyle{ \overline{AB} }[/math]가 수직으로 만나는 점 E에서 선분 AE와 선분EB와의 비율은 원둘레에서 호의 길이의 비율을 보여준다. 따라서 이러한 성질은 선분 AE와 선분EB와의 비율에서 역시 활꼴의 면적을 보여줄 수 있다.
- [math]\displaystyle{ \overline{AB} }[/math]가 원의 중심을 지나 현 [math]\displaystyle{ \overline{CD} }[/math]를 수직이등분할때
- [math]\displaystyle{ \overline{OC}^2 = \overline{CE}^2+ \overline{OE}^2 }[/math]
- [math]\displaystyle{ \overline{OC} = \overline{OB} = \overline{AO} }[/math]
- [math]\displaystyle{ \overline{OB}= \overline{OE} + \overline{EB} }[/math]
따라서
- [math]\displaystyle{ \overline{CE}^2 =\overline{OC}^2 - \overline{OE}^2 }[/math]
- [math]\displaystyle{ \overline{CE}^2 =\overline{AO}^2 - \overline{OE}^2 }[/math]
그리고
- [math]\displaystyle{ \overline{AO}^2 - \overline{OE}^2 = \left( \overline{AO} -\overline{OE}\right) \left(\overline{AO}+ \overline{OE} \right) }[/math]
- [math]\displaystyle{ \overline{AO}^2 - \overline{OE}^2 = \left( \overline{EB}\right) \left(\overline{AE} \right) }[/math]
따라서
- [math]\displaystyle{ \left( \overline{CE}\right) \left(\overline{CE} \right) =\left( \overline{EB}\right) \left(\overline{AE} \right) }[/math]
- [math]\displaystyle{ \left( \overline{CE}\right) \left(\overline{ED} \right) =\left( \overline{EB}\right) \left(\overline{AE} \right) }[/math]이다.
이렇게 현의 길이와 직경(지름)의 길이는 일대일 대응한다.
한편 활꼴의 길이 선분CD와 활꼴의 높이 선분EB를 갖는 활꼴의 길이([math]\displaystyle{ l }[/math])는 높이([math]\displaystyle{ h }[/math])와 직경([math]\displaystyle{ D }[/math])에서 다음의 관계가 있다.
- [math]\displaystyle{ \left( \overline{CE} \right) \left( \overline{ED} \right) = \left( \overline{AE} \right) \left( \overline{EB} \right) }[/math]이다.
- [math]\displaystyle{ \overline{CD} = \overline{CE} + \overline{ED} }[/math]이고 [math]\displaystyle{ \overline{CE} = \overline{ED} }[/math]이므로
- [math]\displaystyle{ \overline{AE} = a, \overline{EB} = b , \overline{CE} =x }[/math]를 가정하고
- [math]\displaystyle{ x^2 = ab }[/math]
- [math]\displaystyle{ x = \sqrt{ab} }[/math]
- [math]\displaystyle{ l = 2x = 2\sqrt{ab} }[/math]이고 [math]\displaystyle{ a =D-b }[/math]이다.
따라서
- [math]\displaystyle{ l = 2\sqrt{(D-b)b} }[/math]
따라서
- [math]\displaystyle{ l = 2\sqrt{(D-b)b} }[/math]
- [math]\displaystyle{ l = \sqrt{4} \sqrt{(D-h)h} }[/math]
- [math]\displaystyle{ l = \sqrt{ \left( 4D h \right) - \left( 4 h^2 \right) } }[/math]
연관[편집 | 원본 편집]
- [참고](유클리드 기하학 원론,구텐베르크 프로젝트,John Casey 1885)http://www.gutenberg.org/files/21076/21076-pdf.pdf?session_id=9bfd9ef535a37ac859a6028f101fa4451e3226cc
- ↑ [참고] (수학방 -원의 방정식,원의 방정식 표준형) https://mathbang.net/454
- ↑ 우리말샘 원 등